海洋中蕴藏着丰富的资源,对海洋资源的开发利用将成为未来的热点方向,因此需要研发出水动力性能优秀的水下仿生机器鱼来对海洋资源进行开发探索[1-4]。然而,从目前的技术来看,人造仿生机器鱼的性能与经历过漫长时间进化的鱼类相比,仍存在许多不足。鱼类巡游时,游泳效率高,且能量消耗低,且在其捕食或遇到危险时,能够快速爆发出较高的速度[5-7]。研究鱼类进行水动力性能,了解其水动力性能的变化规律,对水下机器鱼的研制具有巨大的推进作用。近年来,计算机科学、仿生学和计算流体力学的快速发展和结合,为水下仿生机器鱼的研究提供了强有力的条件[8-10]。计算流体力学(computational fluid dynamics,CFD)主要通过计算机,采用数值方法迭代求解流体力学的控制方程,来模拟和分析流体力学方面的问题[11-15]。同时,随着CFD技术的日趋成熟,采用数值方法对机器鱼进行研究,成果也不断涌现。王志东等[16]通过数值计算,研究了金枪鱼游动及其尾鳍摆动的二维模型,讨论了刚性和柔性尾鳍的不同水动力性能。章永华[17]通过数值模拟,研究了机器鱼尾鳍面积对其摆动时产生推进力大小的影响。Luo等[18-19]提出一种双向流固求解器并对尾鳍的不同结构进行了仿真分析,结果表明,刚度非均匀分布的尾鳍能有效模拟真实鱼类的尾鳍变形特征。然而,上述研究只考虑了机器鱼的材料和结构参数对于机器鱼水阻力特性的影响,未综合考虑机器鱼尾鳍的运动参数等多方面因素,鉴于此,本文以大黄鱼(Larimichthys crocea)尾鳍为仿生对象,建立大黄鱼尾鳍模型,并用计算流体力学方法,研究了该模型在同一水域环境不同运动参数和结构参数下的水动力性能。本文还在尾鳍模型的基础上添加聚乙烯(polyethylene,PE)、聚碳酸酯(polycarbonate,PC)、结构钢(ST)等3种蒙皮材料,研究其对大黄鱼尾鳍模型水动力性能的影响,本研究结果不仅为水下机器鱼的设计和制造提供了科学依据,而且对于其性能和水下作业能力的提高具有积极意义。
1 试验模型及方法
1.1 大黄鱼尾鳍模型的建立
1.1.1 模型数据处理 本研究中大黄鱼样本源于浙江省象山县渔晖大黄鱼养殖专业合作社,样本数据的处理方法为将待测量的大黄鱼放置在标准卡尺板上,拍摄大黄鱼的前视和俯视照片(图1)。

图1 大黄鱼采样图
Fig.1 Sampling diagram of yellow croaker
在大黄鱼的采样图中利用Wolfram Mathematica 14提取其尾鳍背部和腹部轮廓线坐标,以大黄鱼尾鳍前端中心点为坐标原点建立坐标系,用最小二乘法作非线性曲线拟合[20](图2)。大黄鱼尾鳍的背部和腹部轮廓线方程为
yup=38.689 8+0.801 5x-0.023 9x2+5.355 1×10-4x3-5.906 3×10-6x4+3.097 2×10-8x5-6.332 3×10-11x6(R2=0.989 3),
(1)
ydown=-32.870 1-0.479 9x-8.495×10-4x2+1.860 2×10-5x3-6.156 9×10-9x4-1.207 8×10-9x5+6.496 2×10-12x6
(R2=0.978 1)。
(2)
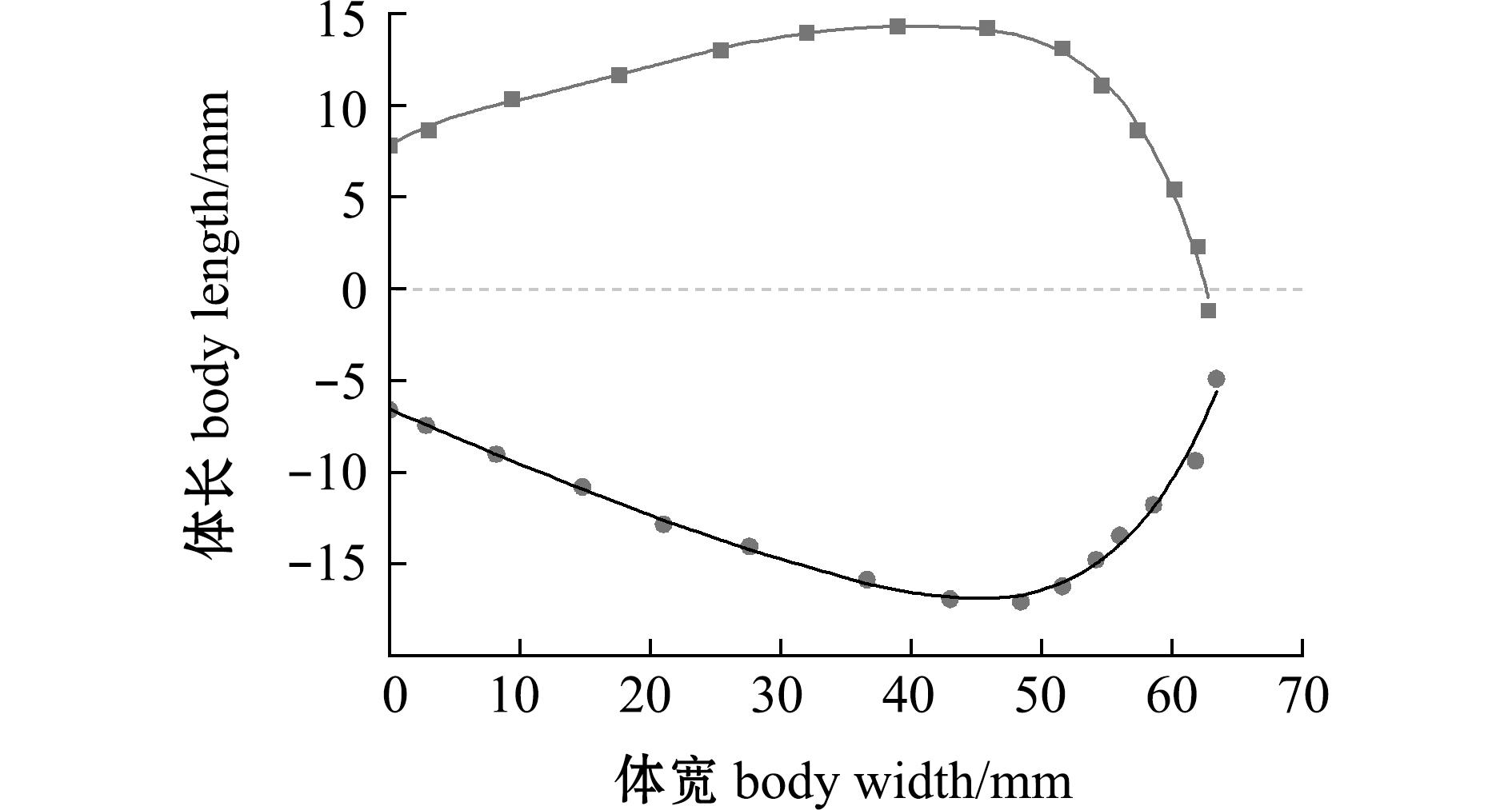
图2 大黄鱼尾鳍背部和腹部轮廓线
Fig.2 Upper and lower contour lines of the circular tail fin of the yellow croaker
式中:yup为大黄鱼尾鳍背部轮廓线体宽方向的坐标;x为大黄鱼体长方向的坐标;ydown为大黄鱼尾鳍腹部轮廓线体宽方向的坐标。
1.1.2 大黄鱼尾鳍模型的建立 基于大黄鱼尾鳍的腹部和背部轮廓线,利用Solidworks 2022软件中绘制样条曲线的方法绘制大黄鱼尾鳍的腹部和背部轮廓,建立大黄鱼尾鳍平面模型,利用放样操作,以大黄鱼尾鳍平面模型为引导线,建立大黄鱼尾鳍三维模型(图3)。大黄鱼尾鳍三维模型的具体参数为尾鳍x方向最大长度为62.4 mm,y方向最大高度为31.2 mm,z方向最大厚度为7.63 mm。蒙皮材料采用FLUENT中的流固耦合材料更改器进行更改,其中PE、PC、ST材料的杨氏模量分别为5E8、2.32E9、2E11 Pa,其泊松比分别为0.42、0.30、0.39。

图3 大黄鱼尾鳍三维模型
Fig.3 3D model of caudal fin of yellow croaker
1.2 流体计算域的建立及试验网格的划分
1.2.1 流体计算域的建立 大黄鱼尾鳍模型位于流体计算域中心,三维流体计算域模型的长度为70 cm、宽度和高度分别为20 cm(图4)。
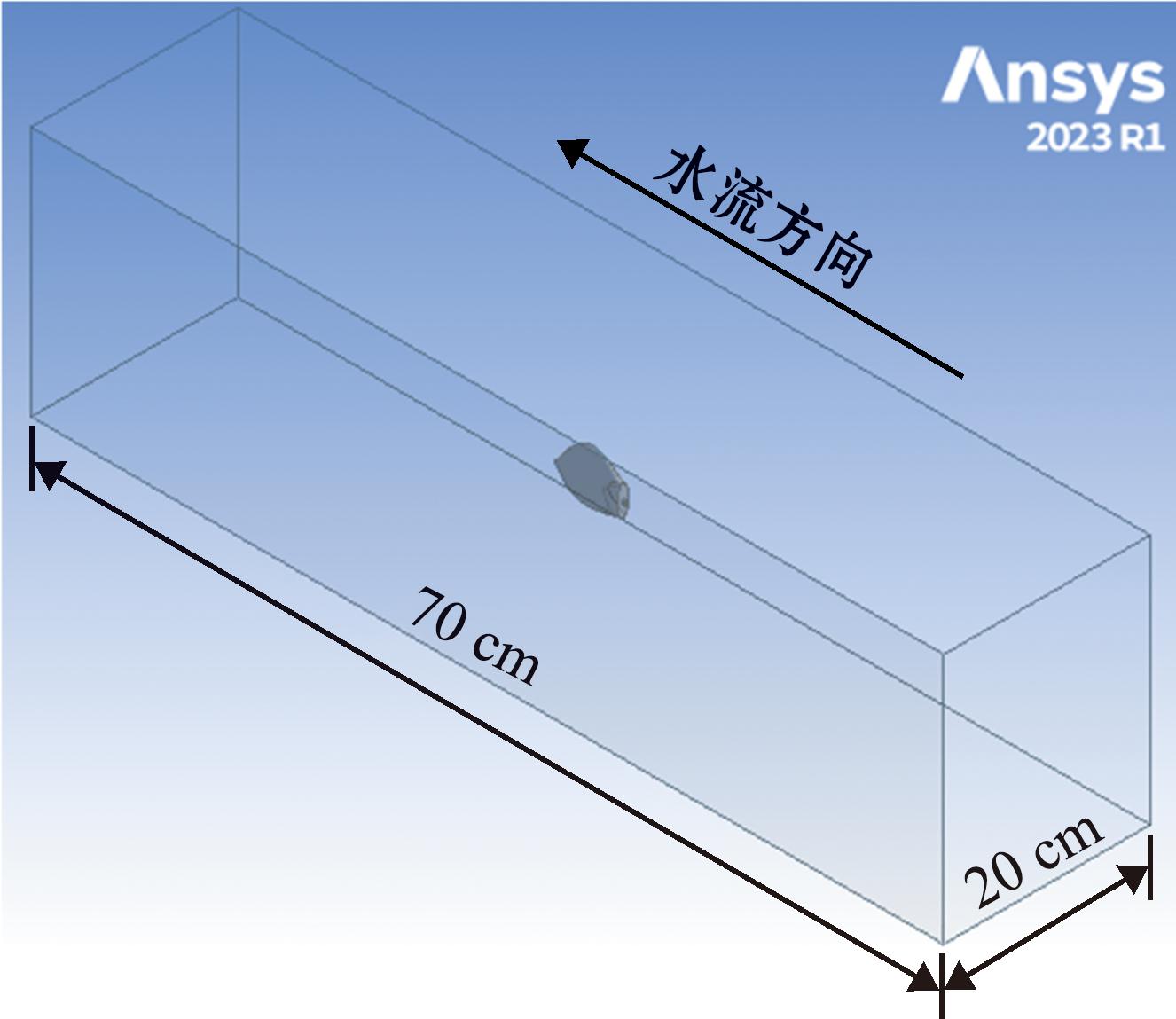
图4 三维流体计算域模型
Fig.4 3D fluid computational domain model
1.2.2 试验网格划分 试验模型中流体计算域的网格划分使用Fluent 2023 R1中的ICEM-CFD,网格划分方法为混合网格划分,流体计算域采用结构化网格划分方法,尾鳍模型采用非结构化网格划分方法[21]。大黄鱼尾鳍模型由封闭曲线构成,因此鱼体模型内部无需进行网格划分[8]。同时,为保证计算正确性和精度,在尾鳍模型加入膨胀层,膨胀层层数为10,增长比为1.1[22]。为了避免外流场的边界效应,将流体计算域模型的边界单元尺寸设置为0.002,大黄鱼尾鳍模型的边界单元尺寸设置为0.001(图5)。

图5 试验网格划分
Fig.5 Experimental grids
网格整体缩放比例为0.4,网格数量为2 074 298。通过划分不同数量网格对比相对误差来验证网格无关性(表1)。
表1 网格无关性验证
Tab.1 Grid-independent verification

网格数量 number of grids相对误差 relative error/% 3 098 3221.6974 289 1321.2335 447 6550.879
1.3 仿真分析方法
基于FLUENT求解器,Zeng等[23]对体长为5~20 cm的大黄鱼研究发现,其临界游泳速度范围为2.5~4.5倍体长/s。大黄鱼尾鳍模型临界游泳速度为0.375~0.675 m/s,故本研究流体域水流速度(v)设为0.5 m/s。
选择计算模型,需结合雷诺数Re计算,雷诺数的计算公式为
(3)
式中:ρ为流体密度(kg/m3),水的密度ρ=998 kg/m3;v为流速(m/s);L为特征长度(mm),L=62.4 mm;μ为水的动力黏度(Pa/s),μ=0.001 Pa/s。
计算得出Re=31 138,其属于湍流形式,考虑仿真试验中尾鳍模型尺寸较小,选择计算模型为RNG k-ε模型[24]。RNG k-ε模型的具体形式为
(4)
(5)
(6)
μeff=μ+μt。
(7)
式中:μt为湍动黏度;ε为湍流耗散度;k为湍流动能;ρ为流体密度;Gk为平均速度梯度引起的湍流动能k的产生项;C1ε和C2ε为经验系数。
大黄鱼尾鳍模型按照正弦规律进行运动,其运动方程为
α(t)=α0+Asin(2πft+α1)。
(8)
式中:α(t)指不同时刻运动的角度;α0指初始时刻角度偏移,本文设置为0;A为摆角幅度;f为摆动频率;α1为初始时刻相位偏移,其值设置为0。在仿真计算中,摆角幅度设置为10°、20°和30°,摆动频率设置为0.5、0.8、1.0 Hz。
基于仿真模型的推进力系数Cx和侧向力系数Cy,其具体形式为
(9)
(10)
式中:Fx(t)和Fy(t)分别表示推进力和侧向力;ρ表示流体密度(kg/m3);v表示来流速度(m/s);S表示尾鳍的迎水面面积(mm2);t表示时间(s)。
仿真试验中尾鳍模型运动的流域为稳态状态下的水流域,FLUENT设置选择压力基求解器,求解器模型为不可压缩流模型,同时因流体计算域模型为水流体流域模型,且仿真试验研究的内容为尾鳍模型在流域内的推进力和侧向力变化,故压力差值采用二阶迎风格式(second order upwind)以提高求解水动力结果的精度[25]。为保证求解过程中的快速稳定,选择在求解过程中能同时更新速度场和压力场的Coupled方法。
FLUENT参数设置中速度入口设置水流速v=0.5 m/s,考虑到重力的影响,重力加速度为9.8 m/s。初始化方案选择标准初始化,初始化的计算参考位置设置为速度入口,参考系设置为相对于单元区域[26]。
1.4 仿真试验流程
不同摆角幅度的水动力试验,基于大黄鱼尾鳍三维模型,设置水流速度v=0.5 m/s,尾鳍的运动频率f=1.0 Hz,模拟仿真了大黄鱼尾鳍在摆角幅度为10°、20°、30°的推进力系数和侧向力系数。
不同运动频率的水动力试验,基于不同摆角幅度的水动力试验结果,设置水流速度v=0.5 m/s,模拟仿真了大黄鱼尾鳍在运动频率为0.5、0.8、1.0 Hz的推进力系数和侧向力系数。
不同厚度的水动力试验,基于不同运动频率的水动力试验,设置水流速度v=0.5 m/s,模拟仿真大黄鱼尾鳍在等厚度和变厚度时的推进力系数和侧向力系数。
不同材料的水动力试验,基于以上试验结果,设置水流速度v=0.5 m/s,选取3种不同的表面蒙皮材料PE、PC、ST,模拟仿真大黄鱼尾鳍模型在改变表面蒙皮材料时的推进力系数和侧向力系数。
1.5 试验方法验证
刘清照[27]通过水槽试验研究了雷诺数为0.4×105时,来流迎角对水轮机叶片的水动力学影响。本文通过CFD仿真试验模拟其水动力对比交叉验证方法的正确性(表2)。
表2 试验方法交叉验证
Tab.2 Cross-validation of experiment methods
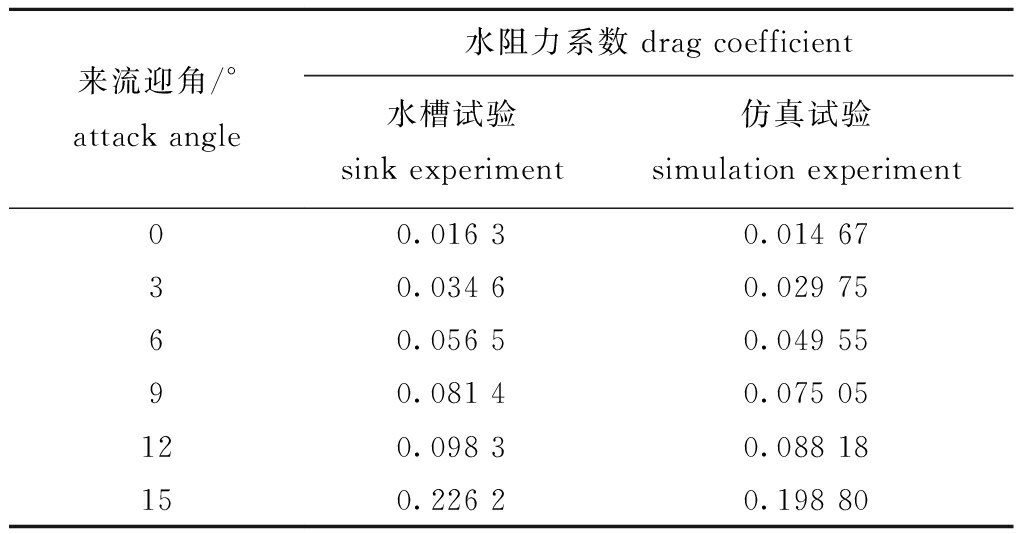
来流迎角/°attack angle水阻力系数 drag coefficient水槽试验sink experiment仿真试验simulation experiment00.016 30.014 6730.034 60.029 7560.056 50.049 5590.081 40.075 05120.098 30.088 18150.226 20.198 80
通过计算验证后得出CFD方法的水动力学试验结果,对比水槽试验的结果相对误差为11.09%±1.29%,小于15%,满足分析要求。
2 结果与分析
2.1 不同摆角幅度下仿生大黄鱼尾鳍水动力性能
不同摆角幅度的大黄鱼尾鳍推进力系数呈现出一种正摆角幅度的趋势,即随着摆角幅度的增加,大黄鱼尾鳍在流域内的推进力系数曲线波动幅值增加(图6)。在水流速度为0.5 m/s时,摆角幅度为10°的大黄鱼尾鳍模型推进力系数范围为-0.318 91~0.271 03;摆角幅度为20°的大黄鱼尾鳍模型推进力系数范围为-0.769 03~1.699 41;摆角幅度为30°的大黄鱼尾鳍模型推进力系数范围为-1.338 80~4.712 43。结果表明,增加大黄鱼尾鳍模型的摆角幅度可有效增加模型的推进力。
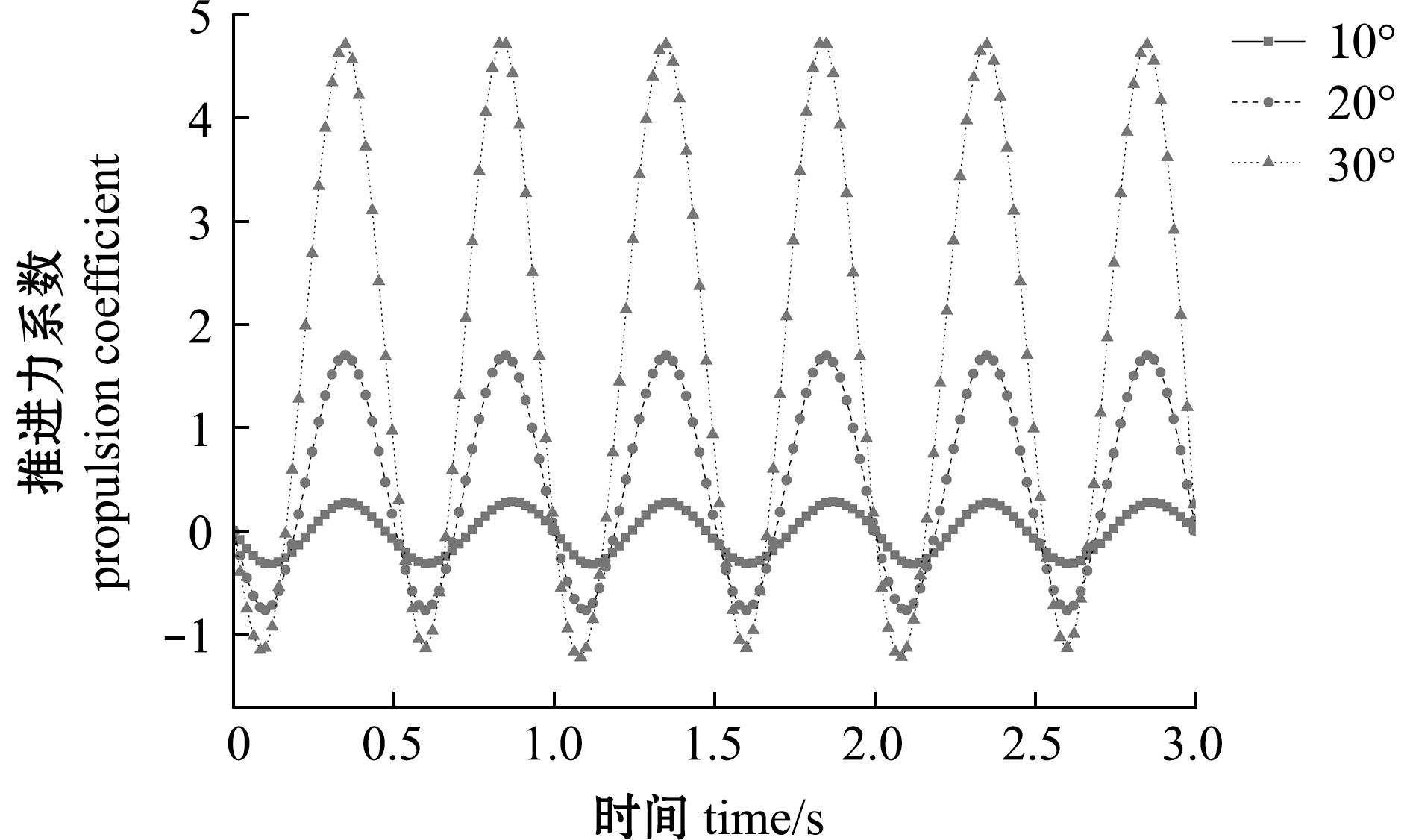
图6 不同摆角幅度的仿生尾鳍推进力系数
Fig.6 Thrust coefficient of bionic caudal fin with different motion angle amplitudes
不同摆角幅度的大黄鱼尾鳍模型侧向力系数也呈现出一种正摆角幅度的趋势,即随着摆角幅度的增加,大黄鱼尾鳍在流域内的侧向力系数曲线波动峰值增加(图7)。在水流速度为0.5 m/s时,摆角幅度为10°的大黄鱼尾鳍模型侧向力系数范围为-7.928 11~7.928 11;摆角幅度为20°的大黄鱼尾鳍模型侧向力系数范围为-13.250 1~13.250 1;摆角幅度为30°的大黄鱼尾鳍模型侧向力系数范围为-24.327 8~24.327 8。结果表明,增加尾鳍摆角幅度,可有效增加尾鳍模型的侧向力。
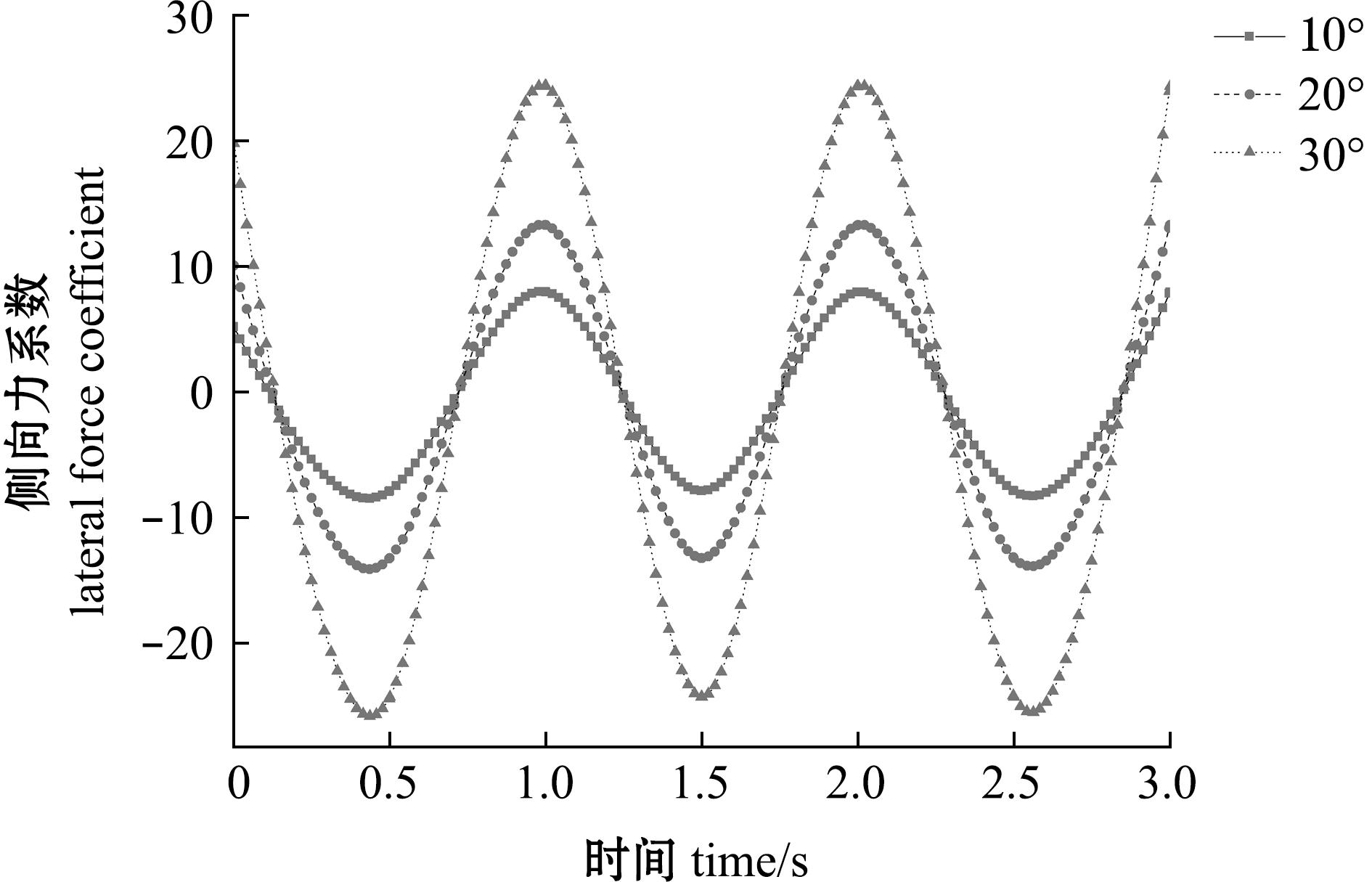
图7 不同摆角幅度的仿生尾鳍侧向力系数
Fig.7 Lateral force coefficient of bionic caudal fin with different motion angle amplitudes
2.2 不同运动频率下大黄鱼仿生尾鳍水动力性能
不同运动频率大黄鱼尾鳍模型的推进力系数呈现出一种正运动频率效应,即随着运动频率的增加,大黄鱼尾鳍的推进力也随之增加(图8)。在水流速度为0.5 m/s时,摆角幅度为30°条件下,运动频率为0.5 Hz时,大黄鱼尾鳍模型的推进力系数范围为-0.996 42~0.996 42;运动频率为0.8 Hz时,大黄鱼尾鳍模型的推进力系数范围为-1.801 08~1.798 09;运动频率为1.0 Hz时,大黄鱼尾鳍模型的推进力系数范围为-1.015 89~4.709 68。结果表明,增大尾鳍模型的运动频率可大幅增加模型的推进力。
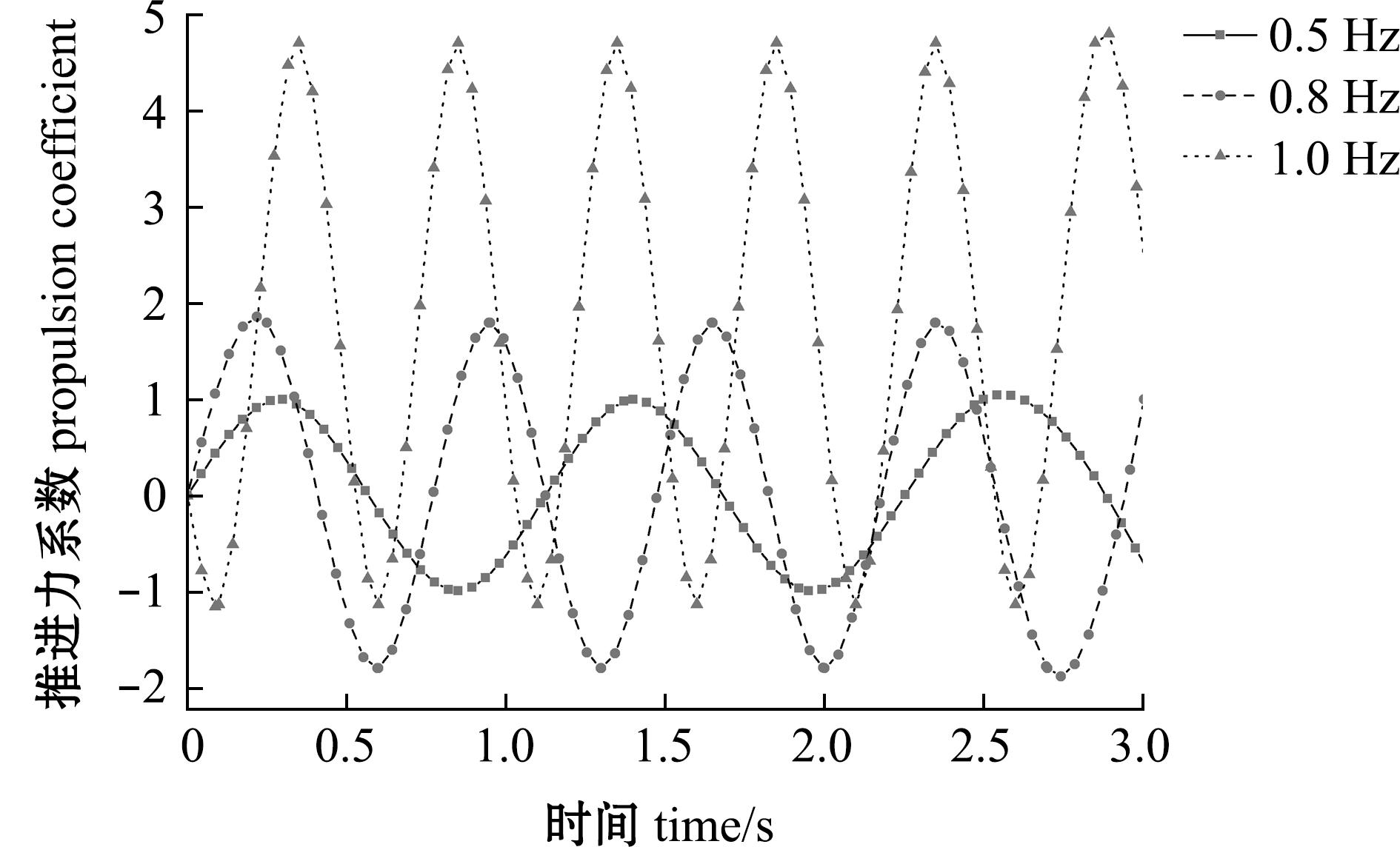
图8 不同运动频率的仿生尾鳍推进力系数
Fig.8 Propulsion coefficient of bionic caudal fin with different motion frequencies
不同运动频率的大黄鱼尾鳍模型的侧向力也呈现出一种正运动频率的效应,即随着运动频率的增加,大黄鱼尾鳍的侧向力也随之增加(图9)。在水流速度为0.5 m/s时,摆角幅度为30°条件下,运动频率为0.5 Hz时大黄鱼尾鳍模型的侧向力系数范围为-7.497 03~7.828 19;运动频率为0.8 Hz时大黄鱼尾鳍模型的侧向力系数范围为-10.759 3~11.289 98;运动频率为1.0 Hz时大黄鱼尾鳍模型的侧向力力系数范围为-25.533 51~24.327 77。
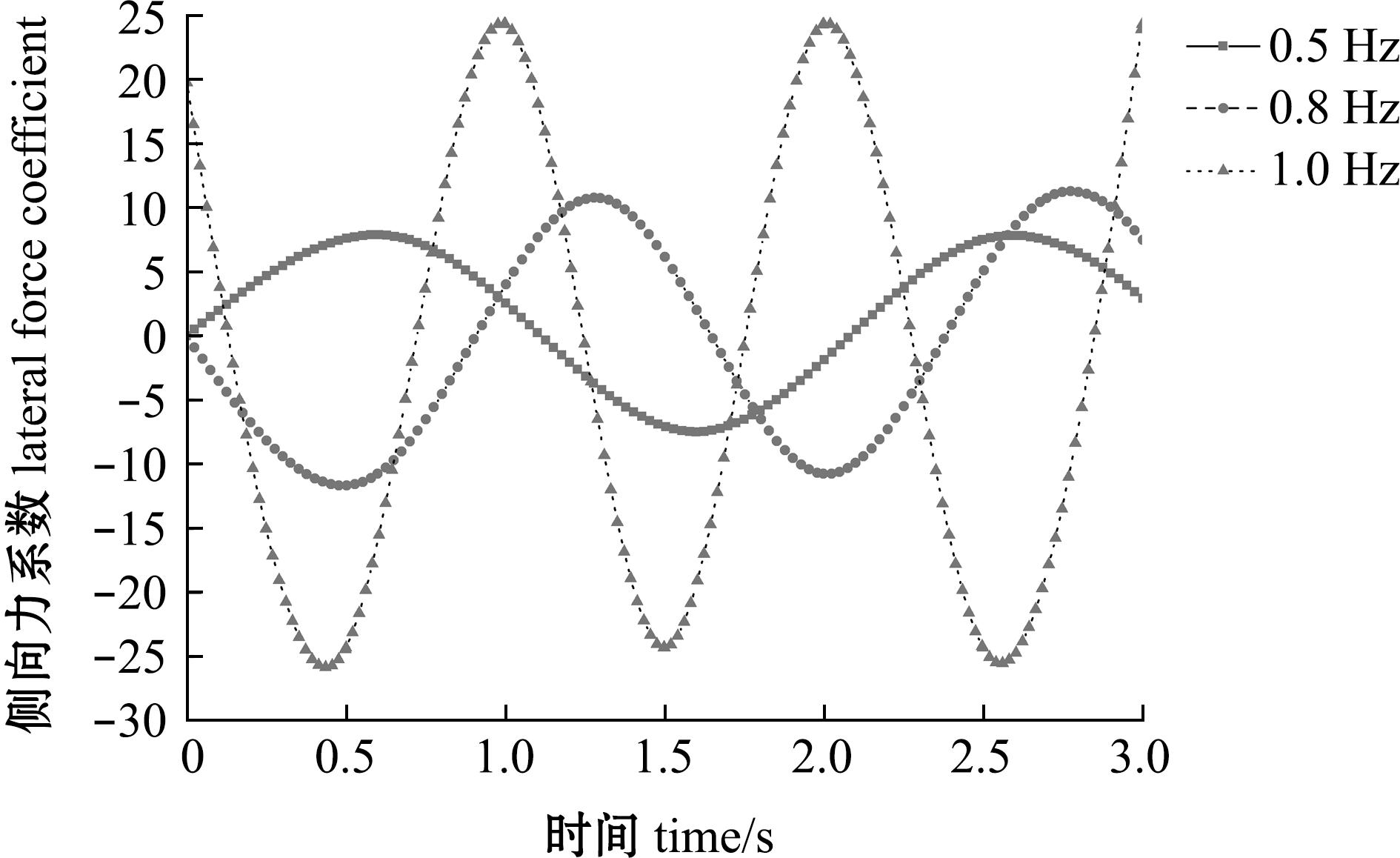
图9 不同运动频率的仿生尾鳍侧向力系数
Fig.9 Lateral force coefficients of bionic caudal fin with different motion frequencies
2.3 不同厚度下大黄鱼仿生尾鳍水动力性能
不同厚度的大黄鱼尾鳍在推进力上呈现出变厚度尾鳍略优于等厚度尾鳍的现象(图10)。在水流速度为0.5 m/s时,运动频率为1.0 Hz、摆角幅度为30°条件下变厚度大黄鱼尾鳍模型的推进力系数范围为-1.133 88~4.716 67;等厚度大黄鱼尾鳍模型的推进力系数范围为-0.870 79~4.350 55。结果表明,变厚度尾鳍的推进力优于等厚度尾鳍的推进力,符合真实鱼体结构。
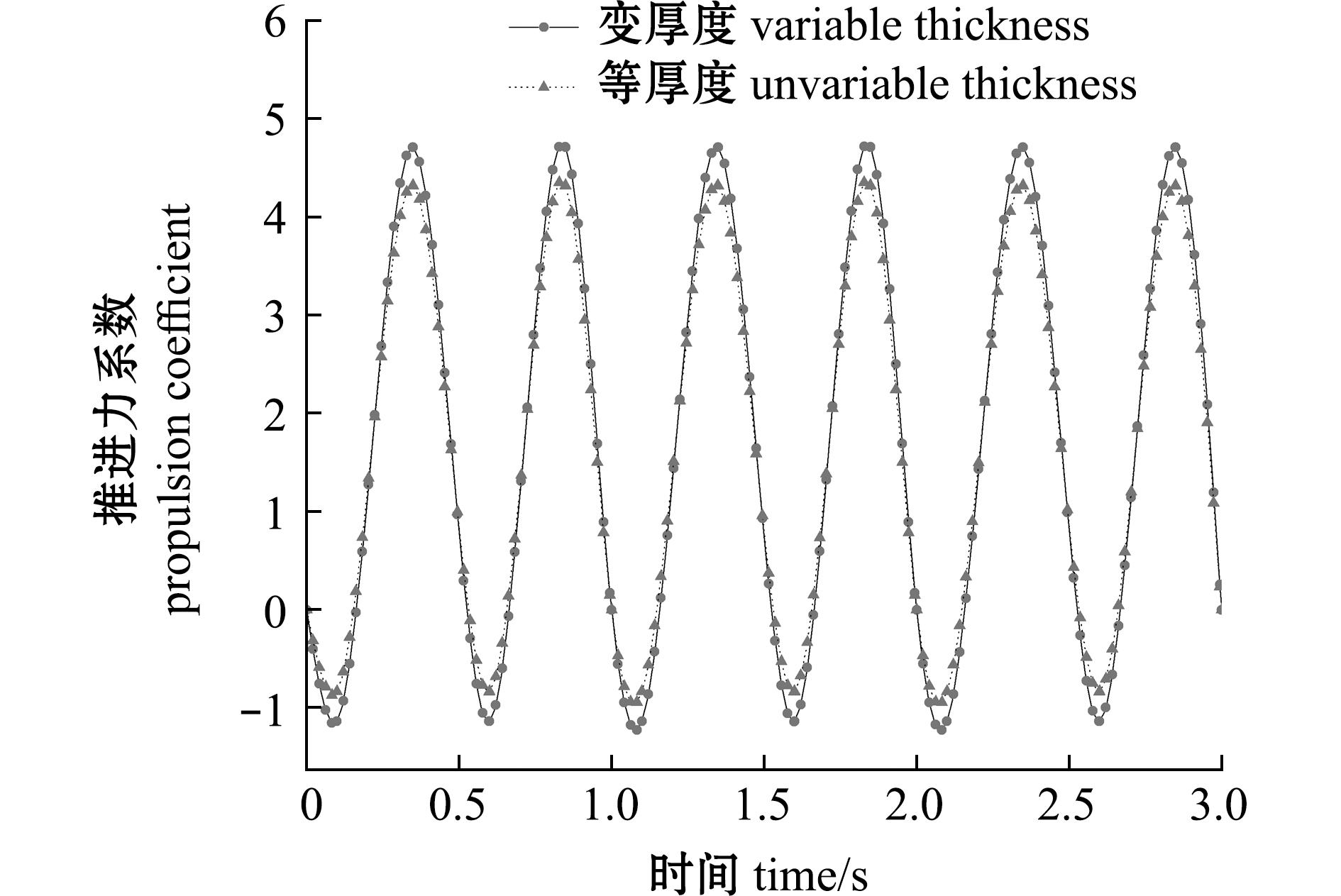
图10 不同厚度的仿生尾鳍推进力系数
Fig.10 Propulsion coefficient of bionic caudal fin with different thicknesses
不同厚度的大黄鱼尾鳍在侧向力上也呈现出变厚度尾鳍略优于等厚度尾鳍的现象(图11)。在水流速度为0.5 m/s时,运动频率为1.0 Hz,摆角幅度为30°条件下变厚度大黄鱼尾鳍模型的侧向力系数范围为-25.856 2~24.327 77;等厚度大黄鱼尾鳍模型的侧向力系数范围为-21.306 3~20.131 62。
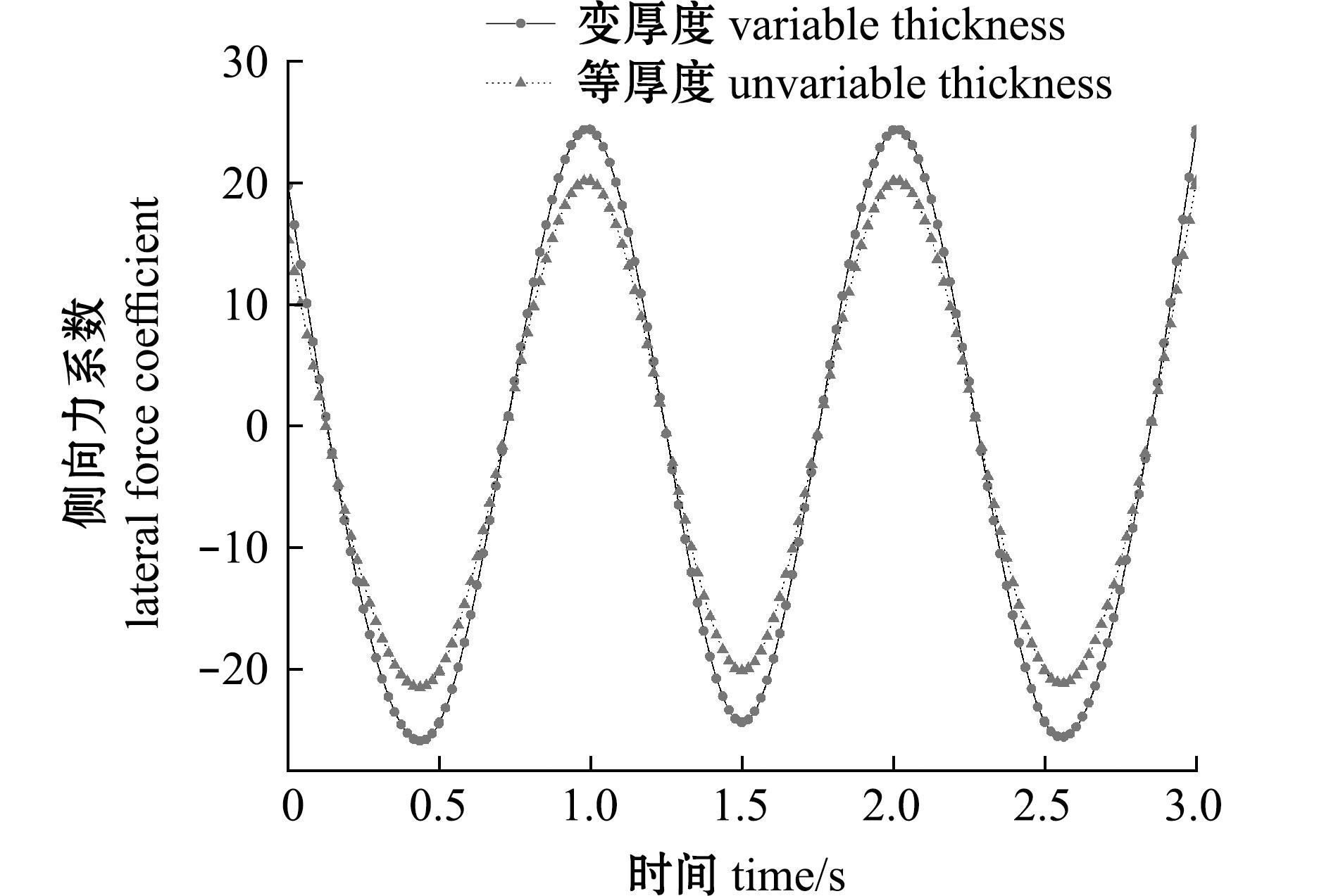
图11 不同厚度的仿生尾鳍侧向力系数
Fig.11 Lateral force coefficients of bionic caudal fin with different thicknesses
2.4 不同材料下大黄鱼仿生尾鳍水动力性能
不同材料的大黄鱼尾鳍在推进力上呈现出PE材料优于PC材料优于ST材料的现象(图12)。在水流速度为0.5 m/s时,运动频率为1.0 Hz,摆角幅度为30°条件下变厚度PE材料大黄鱼尾鳍模型的推进力系数范围为-1.133 88~4.716 67;变厚度PC材料大黄鱼尾鳍模型的推进力系数范围为-0.975 66~4.140 82;变厚度ST材料大黄鱼尾鳍模型的推进力系数范围为-0.898 81~3.886 92。
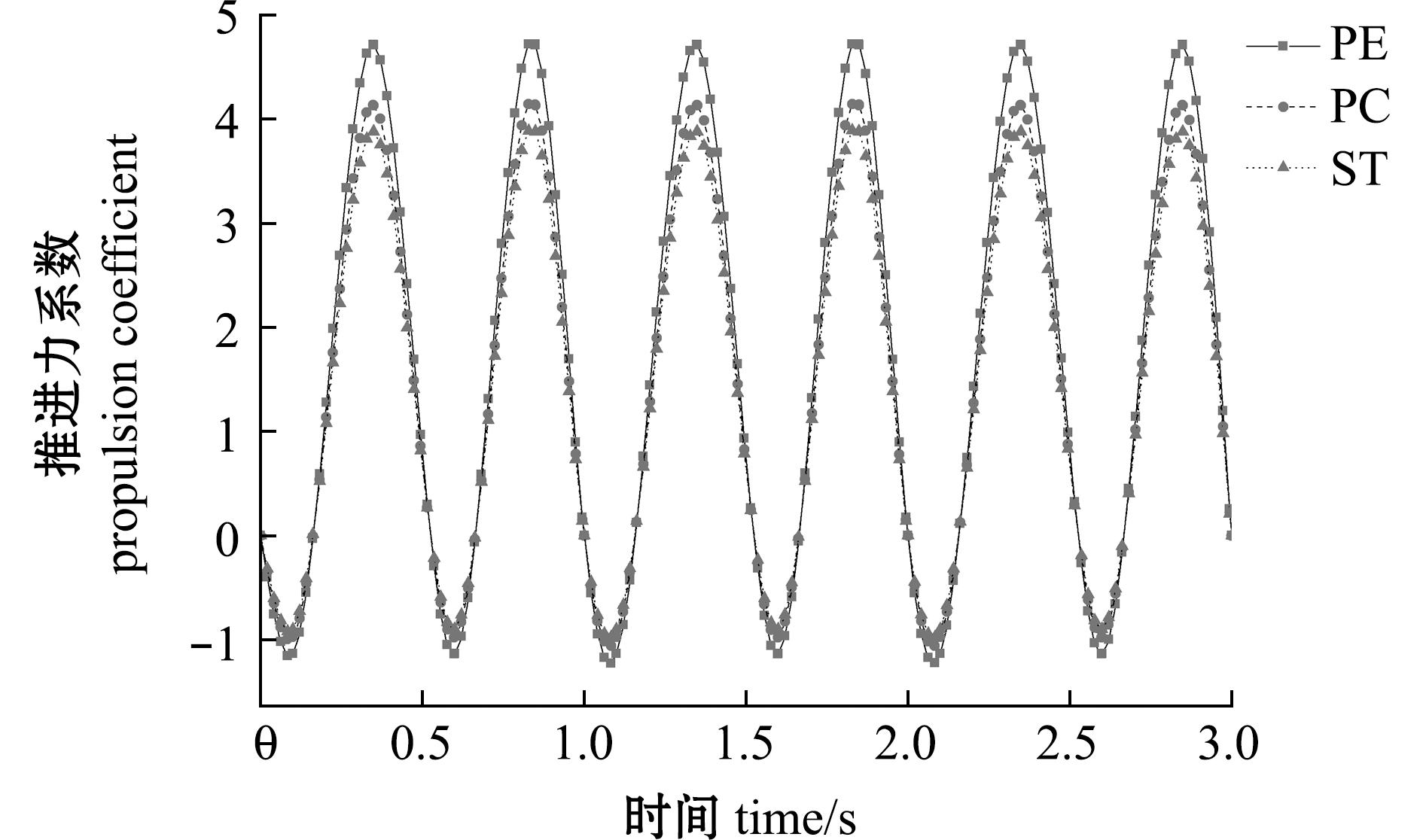
图12 不同材料的仿生尾鳍推进力系数
Fig.12 Propulsion coefficient of bionic caudal fin with different materials
不同材料的大黄鱼尾鳍在侧向力上也呈现出PE材料>PC材料>ST材料的现象(图13)。在水流速度为0.5 m/s时,运动频率为1.0 Hz,摆角幅度为30°条件下变厚度PE材料大黄鱼尾鳍模型的侧向力系数范围为-25.856 2~24.327 77;变厚度PC材料大黄鱼尾鳍模型的侧向力系数范围为-21.929~20.782 62;变厚度ST材料大黄鱼尾鳍模型的侧向力系数范围为-20.016 30~18.997 31。
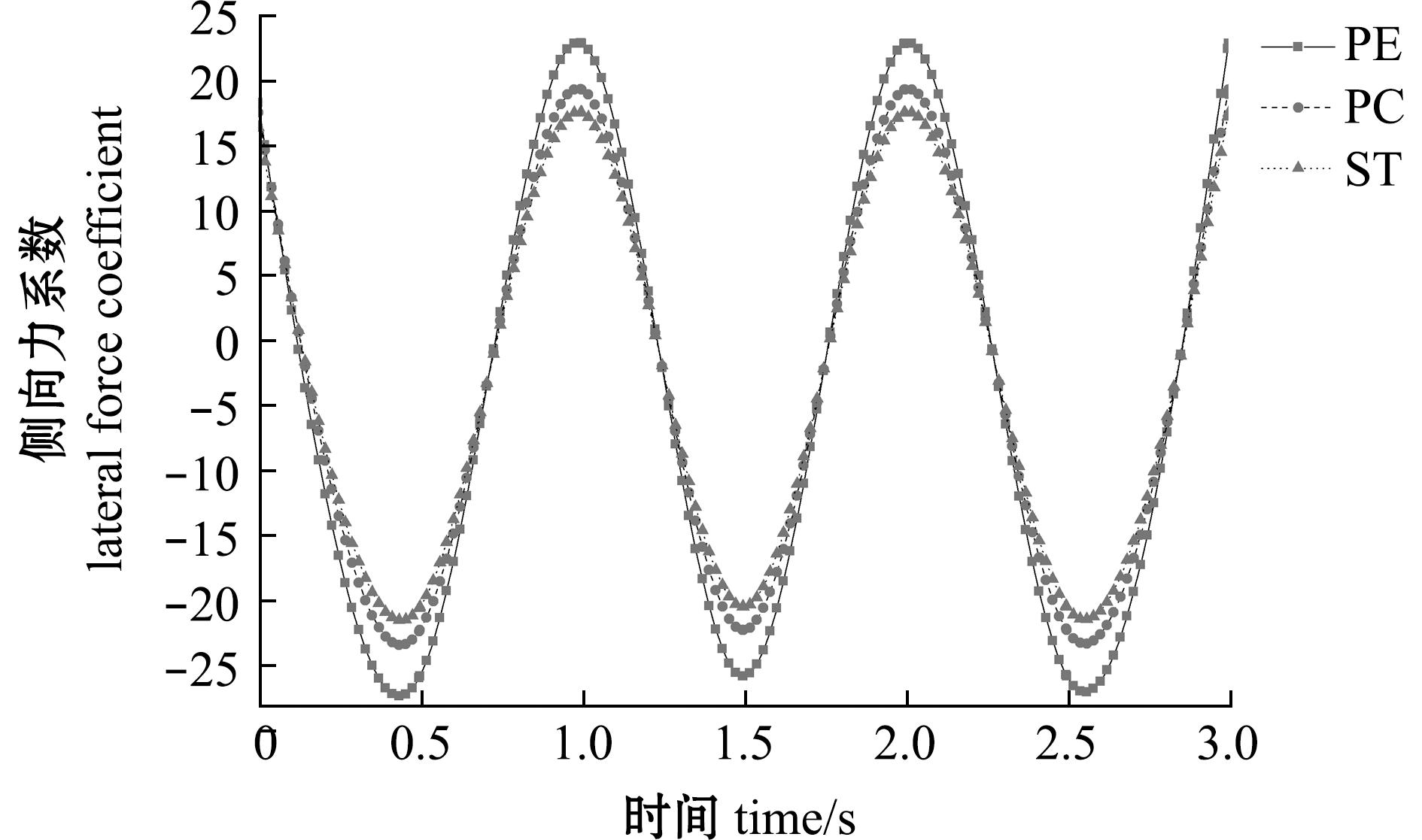
图13 不同材料的仿生尾鳍侧向力系数
Fig.13 Lateral force coefficients of bionic caudal fin with different materials
3 讨论
3.1 不同摆角幅度对大黄鱼仿生尾鳍水动力性能的影响
本研究中基于不同摆角幅度的大黄鱼尾鳍水动力仿真试验,分析了不同摆角幅度对推进力系数和侧向力系数的影响。从推进力系数的变化趋势来看,当尾鳍的摆角幅度为10°时,在水流速度恒定为0.5 m/s的条件下,其推进力系数波动为-0.318 91~0.271 03。当摆角幅度增加到20°时,其推进力系数范围增大至-0.769 03~1.699 41。当摆角幅度达到30°时,推进力系数的波动区间增大,为-1.338 80~4.712 43。从侧向力系数的变化趋势来看,当尾鳍的摆角幅度为10°时,侧向力系数为-7.928 11~7.928 11,显示出一种对称的变化趋势。当摆角幅度提升至20°时,这一范围也相应扩大至-13.250 1~13.250 1。而在30°的摆角幅度下,侧向力系数的变化区间达到了-24.327 8~24.327 8,反映出尾鳍摆动幅度对侧向力系数的显著影响。同时,推进力系数曲线和侧向力系数曲线均呈周期性波动,且推进力系数曲线的波动频率是侧向力系数曲线的2倍。随着摆角幅度的不断增大,推进力系数曲线和侧向力系数曲线的波动幅值均呈增大趋势。且随着摆角幅度的增大,推进力系数呈快速增大趋势,而侧向力系数在摆角幅度小于20°时变化较小,达到30°时明显增大。此结论表明,增大尾鳍摆角幅度可有效提高大黄鱼尾鳍模型的推进力,但在提高推进力的同时,也带来了模型游动的不稳定性。胡瑞南等[28]以鲣(Katsuwonus pelamis)为仿生对象,根据鱼体形态结构建立模型,分析了摆角幅度对模型水动力性能的影响,结果发现,增大摆角幅度贴近真实鱼游动姿态,具有较大的推进力和更优的平衡性,这表明增大摆角幅度可以增大模型的推进力和侧向力,这与本试验中30°摆角幅度的大黄鱼尾鳍模型水动力性能更优的结论一致。本试验揭示了大黄鱼尾鳍模型在不同摆角幅度下的动力学特性,为仿生学研究和鱼类游动机制的理解提供了科学依据。
3.2 不同运动频率对大黄鱼仿生尾鳍水动力性能的影响
本研究中基于不同运动频率的大黄鱼尾鳍水动力仿真试验,分析了大黄鱼尾鳍的不同运动频率对推进力系数和侧向力系数的影响。从推进力系数变化趋势来看,当运动频率为0.5 Hz、摆角幅度保持在30°时,大黄鱼尾鳍模型的推进力系数表现出了显著的波动,其范围为-0.996 42~0.996 42,当运动频率提升至0.8 Hz、推进力系数的范围扩大至-1.801 08~1.798 09,在运动频率达到1.0 Hz时,推进力系数提高更为显著,其推进力系数范围为-1.015 89~4.709 68。从侧向力系数变化趋势来看,当运动频率为0.5 Hz、摆角幅度为30°时,侧向力系数的范围为-7.497 03~7.828 19,当运动频率提升至0.8 Hz,侧向力系数的范围也随之增大,达到-10.759 3~11.289 98,在运动频率为1.0 Hz的情况下,尾鳍模型的侧向力系数范围显著扩大至-25.533 51~24.327 77。同时,随着运动频率的增大,大黄鱼尾鳍模型的推进力系数和侧向力系数均呈增大趋势,推进力系数和侧向力系数在运动频率小于0.8 Hz时变化很小,而当运动频率增大到1.0 Hz时,大黄鱼尾鳍模型的推进力系数和侧向力系数明显增大。此结论表明,增大尾鳍的运动频率可以有效地提高大黄鱼尾鳍模型的推进力和侧向力。唐波[29]基于速度势的面元法对刚性拍动翼不同拍动频率下的水动力进行分析研究,结果表明,推进力随着流速、拍动频率的增大而增加。王志东等[16]基于二维摆动尾鳍模型,研究了不同运动参数对二维尾鳍模型水动力性能的影响,试验结果表明,随着尾鳍运动频率的增加,尾鳍能获得更大的推进力和前进速度。这与本试验中运动频率为1.0 Hz的大黄鱼尾鳍模型的推进力和侧向力更优的结果一致,试验揭示了大黄鱼尾鳍模型在不同运动频率和摆角幅度下的推进力和侧向力特性。
3.3 不同厚度对大黄鱼仿生尾鳍水动力性能的影响
本研究中基于不同厚度的大黄鱼尾鳍水动力仿真试验,分析了大黄鱼尾鳍不同厚度对推进力系数和侧向力系数的影响。从推进力系数的变化趋势来看,对于变厚度的大黄鱼尾鳍模型,其推进力系数展现出了显著的波动,范围为-1.133 88~4.716 67。这一数值区间揭示了尾鳍在推进过程中的复杂力学特性,以及其对于水流速度变化的敏感反应。与此同时,等厚度的尾鳍模型在这一条件下,推进力系数的范围则相对收敛,为-0.870 79~4.350 55,显示出其更为稳定的性能。从侧向力系数的变化趋势来看,变厚度尾鳍模型的侧向力系数波动范围为-25.856 2~24.327 77。这种大幅度变化表明,在侧向稳定性方面,变厚度尾鳍模型面临着更大的挑战。而等厚度尾鳍模型在此条件下的侧向力系数范围则相对较窄,为-21.306 30~20.131 62,显示出更好的侧向稳定性。同时,变厚度尾鳍的推进力系数曲线幅值明显大于等厚度尾鳍,变厚度尾鳍的侧向力系数曲线的幅值比等厚度尾鳍大。结果表明,变厚度柔性尾鳍具有更好的推进性能,此结论符合真实鱼类尾鳍结构的特征。高鑫驰等[30]针对尾鳍摆动仿生机器鱼游动迟缓、姿态不稳定的问题,分析了机器鱼结构参数对机器鱼水动力性能的影响,结果表明,贴近真实鱼结构参数的模型具有更优的水动力性能。这与本试验中变厚度的大黄鱼尾鳍模型相较于等厚度的大黄鱼尾鳍模型具有更高的推进力和侧向力结论一致,本试验为机器鱼尾鳍结构参数的设计提供了新的方向。
3.4 不同材料对大黄鱼仿生尾鳍水动力性能的影响
本研究基于不同材料的大黄鱼尾鳍水动力仿真试验,分析了大黄鱼尾鳍的不同材料对推进力系数和侧向力系数的影响。从推进力系数的变化趋势来看,PE材料尾鳍模型的推进力系数呈现出一个较大的范围,从-1.133 88~4.716 67。这一结果揭示了PE材料在推进力方面的潜力与局限性。PC材料的尾鳍模型同样在1.0 Hz运动频率和30°摆角幅度下,该模型的推进力系数范围为-0.975 66~4.140 82,显示出略低于PE材料的性能。而ST材料的尾鳍模型的推进力系数范围为-0.898 81~3.886 92,这表明ST材料在推进力方面具有更高的稳定性。从侧向力系数的变化趋势来看,PE、PC和ST材料在侧向力系数变化上与推进力系数变化一致,PE材料的尾鳍模型在水流速度为0.5 m/s时,侧向力系数范围为-25.856 2~24.327 77;PC材料的尾鳍模型侧向力系数范围为-21.929~20.782 62;而ST材料的尾鳍模型侧向力系数范围则为-20.016 30~18.997 31。结果表明,PE尾鳍的推进力系数和侧向力系数明显大于PC和ST尾鳍,而PC尾鳍的推进力系数和侧向力系数略大于ST尾鳍。Yun等[31]分析了不同材料下尾鳍的推进特性,并进行了试验验证,结果表明,柔性材料的尾鳍模型具有更优的水动力性能和稳定性。葛飞飞等[32]基于仿生学研究了仿生机器鱼柔性尾鳍的水动力性能,结果表明,柔性强的新月形尾鳍具有较好的推进性能。这与本试验中PE材料的大黄鱼尾鳍模型相较于PC和ST材料的尾鳍模型具有更优的推进力和侧向力一致。
4 结论
1)不同摆角幅度在尾鳍模型的水动力上体现出正摆角幅度的效应,即增大尾鳍的摆角幅度可有效提高大黄鱼尾鳍模型的推进力,但同时也为模型带来了游动的不稳定性。
2)不同摆动频率在尾鳍模型的水动力上体现出正摆动频率的效应,即提高尾鳍的摆动频率可有效提高大黄鱼尾鳍模型的推进力,同时侧向力也有较小的提高。
3)不同厚度的尾鳍模型在水动力上体现出变厚度尾鳍优于等厚度尾鳍的现象,即变厚度尾鳍相较于等厚度尾鳍,具有更好的推进性能,符合真实鱼类尾鳍结构特征。
4)不同材料的尾鳍模型在水动力上体现出PE尾鳍优于PC尾鳍和ST尾鳍的现象,即柔性尾鳍(PE尾鳍)的推进性能优于刚性材料尾鳍。
[1] 周轩,洪波,张玉平.杭州湾东北部鱼类群落优势种时空生态位分析[J].大连海洋大学学报,2023,38(5):848-856.ZHOU X,HONG B,ZHANG Y P.Spatio-temporal ecological niche analysis of the dominant fishes in northeast Hangzhou Bay[J].Journal of Dalian Ocean University,2023,38(5):848-856.(in Chinese)
[2] 李加林,沈满洪,马仁锋,等.海洋生态文明建设背景下的海洋资源经济与海洋战略[J].自然资源学报,2022,37(4):829-849.LI J L,SHEN M H,MA R F,et al.Marine resource economy and strategy under the background of marine ecological civilization construction[J].Journal of Natural Resources,2022,37(4):829-849.(in Chinese)
[3] 史凯文.海洋强国战略下我国海洋科普发展现状与前景展望[J].科技传播,2024,16(1):35-37.SHI K W.Present situation and prospect of marine science popularization in China under the strategy of strengthening the country by sea[J].Public Communication of Science &Technology,2024,16(1):35-37.(in Chinese)
[4] 巴尧骥,唐峰华,张胜茂,等.无人船技术发展现状及其在渔业中的应用[J].大连海洋大学学报,2024,39(5):888-904.BA Y J,TANG F H,ZHANG S M,et al.Current status of development and application of unmanned vessel technology in fisheries:a review[J].Journal of Dalian Ocean University,2024,39(5):888-904.(in Chinese)
[5] 王扬威,王振龙,李健.仿生机器鱼研究进展及发展趋势[J].机械设计与研究,2011,27(2):22-25,32.WANG Y W,WANG Z L,LI J.Research development and tendency of biomimetic robot fish[J].Machine Design &Research,2011,27(2):22-25,32.(in Chinese)
[6] 孙伟,柳素娉,吴罡,等.鱼类游动机理研究进展[J].大连海洋大学学报,2024,39(4):698-707.SUN W,LIU S P,WU G,et al. Research progress of fish swimming mechanism[J]. Journal of Dalian Ocean University,2024,39(4):698-707. (in Chinese)
[7] 刘军考,陈在礼,陈维山,等.水下机器人新型仿鱼鳍推进器[J].机器人,2000,22(5):427-432.LIU J K,CHEN Z L,CHEN W S,et al.A new type of underwater turbine imitating fish fin for underwater robot[J].Robot,2000,22(5):427-432.(in Chinese)
[8] VICTOR NUNES DE SOUSA J,ROBERTO LINS DE MAC DO A,FERREIRA DE AMORIM W Jr,et al.Numerical analysis of turbulent fluid flow and drag coefficient for optimizing the AUV hull design[J].Open Journal of Fluid Dynamics,2014,4(3):263-277.
DO A,FERREIRA DE AMORIM W Jr,et al.Numerical analysis of turbulent fluid flow and drag coefficient for optimizing the AUV hull design[J].Open Journal of Fluid Dynamics,2014,4(3):263-277.
[9] KRAMER M O.Boundary layer stabilization by distributed damping[J].Naval Engineers Journal,1962,74(2):341-348.
[10] DIVSALAR K.Improving the hydrodynamic performance of the SUBOFF bare hull model:a CFD approach[J].Acta Mechanica Sinica,2020,36(1):44-56.
[11] 阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社,2006.YAN C.Computational fluid dynamics method and its application[M].Beijing:Beijing University of Aeronautics &Astronautics Press,2006.(in Chinese)
[12] 邓小刚,宗文刚,张来平,等.计算流体力学中的验证与确认[J].力学进展,2007,37(2):279-288.DENG X G,ZONG W G,ZHANG L P,et al.Verification and validation in computational fluid dynamics[J].Advances in Mechanics,2007,37(2):279-288.(in Chinese)
[13] 刘必林,黄小双,陈新军,等.计算流体力学方法在仿生机器鱼中的应用研究进展[J].大连海洋大学学报,2024,39(4):719-728.LIU B L,HUANG X S,CHEN X J,et al.Research advances on application of computational fluid dynamics methods in bionic robotic fish:a review[J].Journal of Dalian Ocean University,2024,39(4):719-728.(in Chinese)
[14] 田昌凤,刘兴国,车轩,等.基于CFD数值模拟的单罐真空吸鱼泵研制[J].大连海洋大学学报,2022,37(6):1046-1054.TIAN C F,LIU X G,CHE X,et al.Development of a single-tank vacuum fish pump based on computer fluid dynamic (CFD) numerical simulation[J].Journal of Dalian Ocean University,2022,37(6):1046-1054.(in Chinese)
[15] 初文华,武树龙,王一博,等.基于流固耦合算法的不同材料网板水动力试验[J].渔业现代化,2024,51(3):79-88.CHU W H,WU S L,WANG Y B,et al.Hydrodynamic experiment of different materials otter board based on fluid-structure coupling algorithm[J].Fishery Modernization,2024,51(3):79-88.(in Chinese)
[16] 王志东,丛文超,张淋,等.自主航行模式下二维摆动尾鳍的推进性能研究[J].江苏科技大学学报(自然科学版),2010,24(6):523-528.WANG Z D,CONG W C,ZHANG L,et al.Propulsion performance of 2D oscillating caudal fin under the autonomous navigation mode[J].Journal of Jiangsu University of Science and Technology (Natural Science Edition),2010,24(6):523-528.(in Chinese)
[17] 章永华.尾鳍面积对摆动推进力大小的影响[J].轻工机械,2019,37(6):39-43.ZHANG Y H.Influence of caudal fin area on thrust generation during oscillating motion[J].Light Industry Machinery,2019,37(6):39-43.(in Chinese)
[18] LUO Y,XIAO Q,SHI G Y,et al.A fluid-structure interaction solver for the study on a passively deformed fish fin with non-uniformly distributed stiffness[J].Journal of Fluids and Structures,2020,92:102778.
[19] LUO Y,XIAO Q,SHI G Y,et al.The effect of variable stiffness of tuna-like fish body and fin on swimming performance[J].Bioinspiration &Biomimetics,2020,16(1):016003.
[20] 陈宏.仿生机器鱼巡游和机动的运动机理研究[D].合肥:中国科学技术大学,2006.CHEN H.Research on the motion mechanism of bionic robot fish in cruise and maneuver[D].Hefei:University of Science and Technology of China,2006.(in Chinese)
[21] 韩占忠,王敏,兰小平.FLUENT:流体工程仿真计算实例与应用[M].北京:北京理工大学出版社,2004.HAN Z Z,WANG M,LAN X P.FLUENT:fluid engineering simulation calculation example and application[M].Beijing:Beijing Insititute of Technology Press,2004.(in Chinese)
[22] 李辉,申胜男.流体力学仿真软件ANSYS Fluent在工程中的应用[M].北京:科学出版社,2019.LI H,SHEN S N.Application of ANSYS Fluent, a fluid mechanics simulation software, in engineering[M].Beijing:Science Press,2019.(in Chinese)
[23] ZENG J J,LIU W,DENG Y C,et al.Swimming performance in large yellow croaker:effects of group size,test protocol,and recovery time on critical swimming speed[J].Marine Biotechnology,2024,26(2):380-388.
[24] 王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004.WANG F J. Computational fluid dynamics analysis:principles and applications of CFD software [M].Beijing:Tsinghua University Press,2004.(in Chinese)
[25] CANDELIER F,BOYER F,LEROYER A.Three-dimensional extension of Lighthill’s large-amplitude elongated-body theory of fish locomotion[J].Journal of Fluid Mechanics,2011,674:196-226.
[26] 耿文豹,魏永康,洪树峰,等.仿生机器鱼外形设计及流场阻力数值分析[J].数字海洋与水下攻防,2024,7(3):318-325.GENG W B,WEI Y K,HONG S F,et al.Shape design and numerical analysis of flow field resistance of bionic robot fish[J].Digital Ocean &Underwater Warfare,2024,7(3):318-325.(in Chinese)
[27] 刘清照.潮流能水轮机仿生叶片水动力研究[D].大连:大连理工大学,2018.LIU Q Z. Research on hydrodynamics of tidal turbine bionic blades[D].Dalian:Dalian University of Technology,2018.(in Chinese)
[28] 胡瑞南,梅杰,程正树,等.尾鳍摆动驱动仿生机器鱼的水动力性能仿真分析[J].武汉科技大学学报,2020,43(6):463-470.HU R N,MEI J,CHENG Z S,et al.Simulation analysis of hydrodynamic performance of bionic robotic fish driven by caudal fin swing[J].Journal of Wuhan University of Science and Technology,2020,43(6):463-470.(in Chinese)
[29] 唐波.仿生拍动水翼的水动力性能研究[D].哈尔滨:哈尔滨工程大学,2008.TANG B.Hydrodynamics analysis of a bionic flapping hydrofoil[D].Harbin:Harbin Engineering University,2008.(in Chinese)
[30] 高鑫驰,梅杰,祁靖媛,等.仿生机器鱼胸尾鳍联动水动力学性能分析[J].起重运输机械,2023(13):21-30.GAO X C,MEI J,QI J Y,et al.Hydrodynamic performance analysis of linkage by pectoral and caudal fins of bionic robot fish[J].Hoisting and Conveying Machinery,2023(13):21-30.(in Chinese)
[31] YUN D,KIM K S,KIM S.Thrust characteristic of a caudal fin with spanwise variable phase[J].Ocean Engineering,2015,104:344-348.
[32] 葛飞飞,沈灿,谢鸥.柔性尾鳍的形状对仿生机器鱼水动力学特性的影响研究[J].现代制造工程,2024(8):35-41.GE F F,SHEN C,XIE O.Study on the effect of flexible caudal fin shape on the hydrodynamic characteristics of bionic robotic fish[J].Modern Manufacturing Engineering,2024(8):35-41.(in Chinese)