现代化海洋牧场是基于海洋生态系统[1]，利用现代科学技术支撑和运用现代管理理念与方法进行管理，最终实现生态良好、资源丰富和产品安全的可持续发展的现代海洋渔业生产方式[2]。渔业资源评估是指利用声学、光学和遥感信息等技术对海洋生物资源进行探测和评估，且贯穿海洋牧场开发过程的重要活动[3-4]，可为海洋牧场前、中、后期的建设提供理论依据和技术指导。当前海洋牧场渔业资源评估主要采用捕捞采样或潜水员水下观测方法，但这些方法存在安全性差、工作强度大、采样不全面和评估结果粗糙等局限性。为此，随着水下机器人技术的日益成熟，人们开始尝试使用单台自主水下机器人(AUV)作为观测探测移动平台进行渔业资源调查、评估，并取得了良好的效果。然而，渔业资源评估通常需要覆盖较大海域，随着时间动态变化，此过程具有高度的不确定性，面对高时效、大尺度的任务需求，单水下机器人变得力不从心，难以满足要求，而多水下机器人系统所具有空间分布性、系统冗余性、时间高效性和执行协调性等特点，是渔业资源评估的一种潜在有效手段，具有单水下机器人无法比拟的优越性。
多水下机器人系统的分布性、冗余性为其工程应用带来优势的同时，也增加了系统控制的难度，其中关键问题之一便是多水下机器人编队控制，对此国内外学者予以了广泛关注。当前传统多水下机器人编队控制方法，如领航者-跟随者法[5]、虚拟结构法[6]和人工势场法[7]等已经逐渐具备了较为成熟的理论基础。Li等[8]提出一种欠驱动水下机器人的编队控制方法，通过一种星形拓扑声学通信网络，将每个节点视为特定水下机器人的虚拟领导者，并分配自身的轨迹以形成编队。Song等[9]推导了一个基于经验的编队控制律，并提出了一种有限时间分布式观测器，供跟随者估计领导者的位置，以实现基于位置估计的编队控制。孙栋等[10]针对已知路径提出领航者-虚拟结构策略，跟随者水下机器人采用基于通信时延补偿的滑模控制器进行跟踪，以形成多水下机器人的可重构编队控制。然而，这类方法往往依赖于环境模型和机器人的运动学或动力学模型，由于水下环境的复杂性及洋流等外界因素，精确的环境信息及模型难以获得，因此难以在实际的多水下机器人平台中使用[11]。
近年来，深度强化学习因其无须精确运动学模型即可通过环境交互学习控制策略的特性，逐渐被应用于多机器人编队控制，并在仿真环境中取得了良好效果[12-13]。在海洋牧场资源评估领域，利用多自主水下机器人(AUV)协同观测显著提升了渔业资源评估的准确性和效率[14]。通过深度强化学习优化路径规划和任务分配，这些AUV可以在广阔海域中有效开展资源监测和数据采集[15]。
现有多机器人编队控制方法多基于领航者-跟随者架构。如Knopp等[16]提出的GQ(λ)算法通过视觉信息来学习编队控制，在仿真和应用中表现良好，尤其在海洋牧场和水产养殖领域实现了多机器人系统的协作监测和管理[17]，但其对环境光照和视觉传感器的稳定性高度依赖，导致在复杂水下环境中适应性不足。赵启等[18]使用深度强化学习D3QN算法，将优先选择策略与多层动作库结合以加速僚机学习保持编队，但该方法在多变环境下学习效率仍然有限，缺乏自适应灵活性，且主要依赖集中式控制，缺乏分布式执行能力。Zhao等[19]提出的改进随机制动深度强化学习(DRLRB)方法虽实现了多欠驱动无人水面舰艇的路径跟随，但对动力学模型的依赖限制了其在复杂环境中的泛化能力。Xie等[20]基于优势深度确定性策略梯度算法(ADDPG)建立了固定编队形状的控制模型，但该方法行为灵活性有限，难以满足动态任务需求。
综上，本文提出了一种基于MADDPG的多水下机器人编队控制方法。该方法将N个水下机器人划分为领航者和跟随者，通过领航者-跟随者架构的MDP模型实现编队控制。机器人利用自身和其他机器人的位置、速度等信息进行观测，并通过受力表达其动作。奖励函数设计上结合了领航者与目标位置的距离、跟随者之间的距离等因素，兼顾个体和系统的奖励结果表明，该方法能够形成类似生物群体的协同运动模式，在编队稳定性和路径优化方面优于其他算法，且无需依赖精确的运动学模型，具有灵活性、分布式执行能力和强泛化能力。该方法降低了感知需求并提升学习效率，在动态环境下表现出卓越的策略生成能力。同时，该方法在资源稀少或分布不均的海洋牧场环境中展现出灵活性和泛化能力，为复杂海洋任务中的多机器人协作问题提供了新思路。未来研究可结合更多智能算法与感知技术，进一步提升方法的适用性与协同效能，以应对更复杂的海洋环境和任务需求。
1 问题描述
本文关注多水下机器人在海洋资源评估过程中的编队控制问题，即具有随机初始位姿的水下机器人形成编队并协调一致地运动到指定的目标点。考虑到每台水下机器人具有较为独立的感知和行动能力，可将其视为一个智能体，为此，本文将多水下机器人的协同控制问题抽象为多智能体强化学习问题。
1.1 基于领航者-跟随者控制架构的MDP建模
由于每台水下机器人无法获取全局信息，只能依赖局部信息进行策略学习和决策，为此，本文基于部分可观察马尔可夫决策过程(POMDP)框架[21]，对多水下机器人编队控制问题进行建模，以更好地适应海洋资源评估任务中的不确定性和局部观测限制。同时，考虑到领航者-跟随者架构具有结构稳定简单且易于实现等优点，故将此结构引入MDP框架中，构建基本领航者-跟随者控制架构的部分可观察的马尔科夫决策过程，具体定义为元组〈N，S，A，R，Ω，P〉，其中：
N为海洋牧场资源评估的水下机器人数量；
S为状态有限集，其中初始状态为S0；
A为水下机器人联合动作的集合，A=AL×AFi×…×AFn。其中AL为领航者水下机器人的动作，AFi为第i个跟随者水下机器人的动作；
R为奖励函数，反映机器人在海洋资源评估任务中的表现，RL为领航者水下机器人的奖励函数，RF为跟随者水下机器人的奖励函数；
Ω为所有水下机器人对海洋环境的联合观察的有限集，Ω=OL×OFi×…×OFn。其中，OL为领航者水下机器人的观察集，OFi为第i个跟随者水下机器人的观察集；
P为概率转移函数；
基于提出的MDP，可以使用多水下机器人深度强化学习来找到可以产生编队控制的局部运动策略。具体而言，由于编队控制可以被看作个体之间协调控制的结果，因此，寻找局部运动策略可以当成最大化其总累积奖励的优化问题，其表达式为
。
(1)
式中：R(St，At，St+1)和
分别为系统级和个体级的奖励函数，At为t时刻的水下机器人群体联合动作，π(i)为第i个水下机器人的局部策略。系统级奖励可以反映资源评估任务的整体目标，而个体级奖励可以帮助细化不同水下机器人在资源监测任务中的贡献。在一个任务中可能具有系统级奖励函数与个体级奖励函数其中之一，或这两者兼而有之。
1.2 水下机器人位置更新描述
考虑到水下机器人作业时通常保持相同深度，本文假设水下机器人定深运动，并将其编队控制任务简化为二维平面内的移动，同时考虑非完整约束[22](图1)。每个水下机器人的状态更新可以描述为
(2)
(3)
(4)
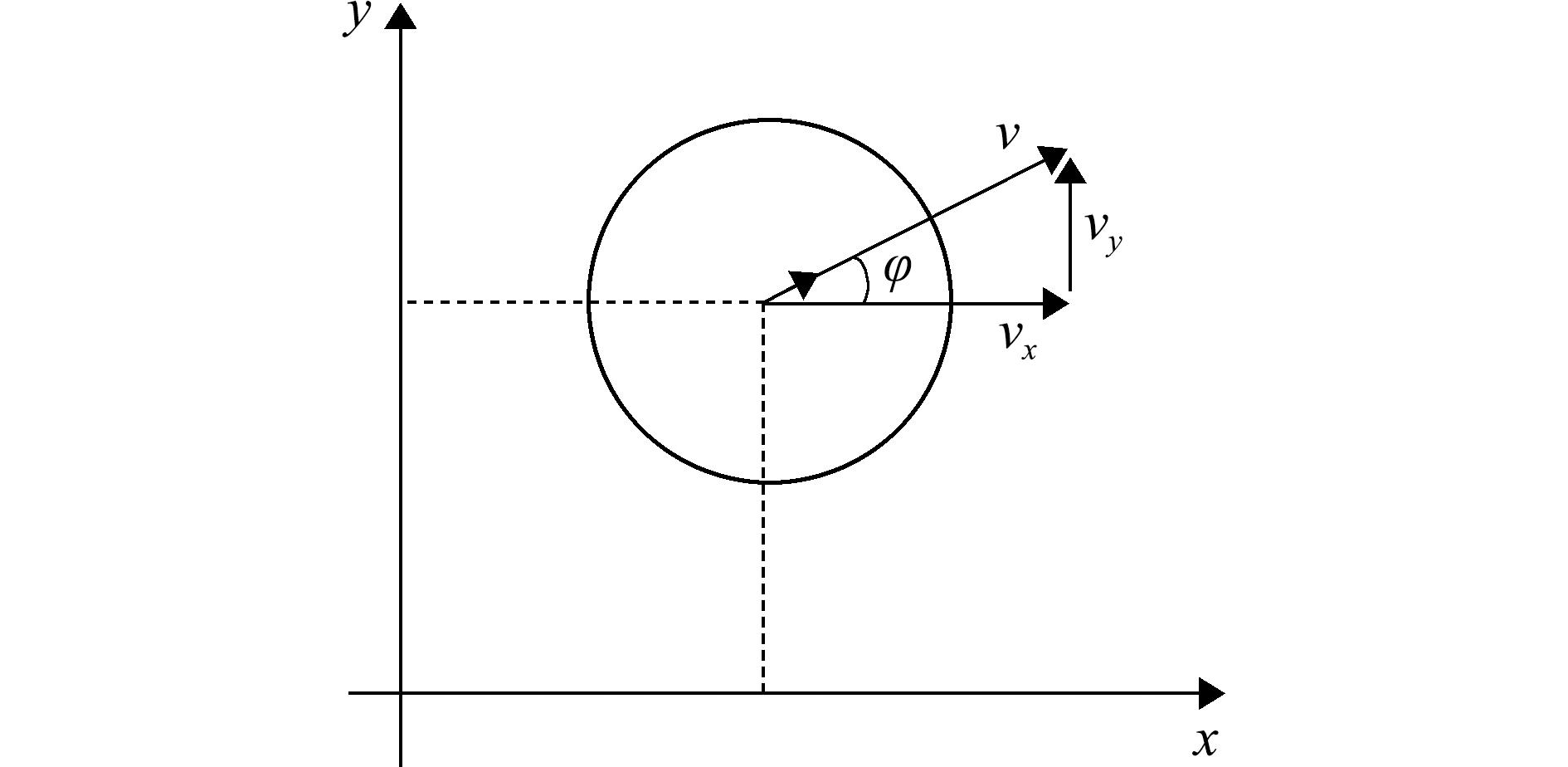
图1 水下机器人的运动分析
Fig.1 Motion analysis of underwater robots
式中：pt+1、vt+1和φt+1分别表示水下机器人下一时刻的位置、速度和航向角参数；x与y表示横纵坐标；上标t代表时间；Δt为时间间隔；a为水下机器人的加速度。假设水下机器人的最大速度和加速度分别为vmax和amax。
2 方法与应用
考虑到MADDPG高效的学习性能、强大的稳定性和适应性，以及在多智能体环境中处理连续动作空间和复杂交互的能力，本文使用MADDPG实现多水下机器人的编队控制，具体而言，水下机器人被划分为领航者和跟随者两类，各自任务不同，且局部控制策略通过强化学习训练获得。领航者通过集中式训练提供全局指引，确保方向控制；跟随者则基于局部信息调整位置，以维持编队结构的稳定性。为此，在本节中首先介绍水下机器人个体局部运动策略训练与应用总体框架；其次，介绍水下机器人的状态、观测与动作表示；然后，根据编队控制的任务设计领航者水下机器人和跟随者水下机器人的立即奖励函数，从系统层面和个体层面共同引导水下机器人的运动策略学习。最后，介绍MADDPG算法、水下机器人决策网络组件的具体内容及算法流程。
2.1 基于MADDPG的多水下机器人编队控制方法总体框架
基于MADDPG的多水下机器人编队控制方法总体框架如图2所示，此框架分为训练阶段和推理阶段。在训练阶段，领航者决策网络与N-1个跟随者决策网络分别为领航者水下机器人和每一个跟随者水下机器人输出动作来与环境及其他水下机器人进行交互，水下机器人在执行完该动作后得到新的观测状态信息及应得的奖励或惩罚。将这些交互数据存入到经验池中，当有足够的数据存入后，从经验池中用随机采样的方式得到交互数据，用于迭代更新这些决策网络。值得注意的是，在训练决策网络时关注了部分水下的干扰，通过引入随机噪声向量替代，使得水下机器人执行随机动作以促进探索水下的未知环境。另一个手段为每个水下机器人从不同的初始状态开始探索，可在本质上降低探索经验的重复率。多个水下机器人可以更快地探索不同的运动状态，且可以更快地积累经验池中的训练数据，加速水下机器人策略网络的训练进程。这种训练方式使得水下机器人能够快速学习在资源评估任务中的最佳动作决策，确保对目标区域的高效覆盖和数据采集。
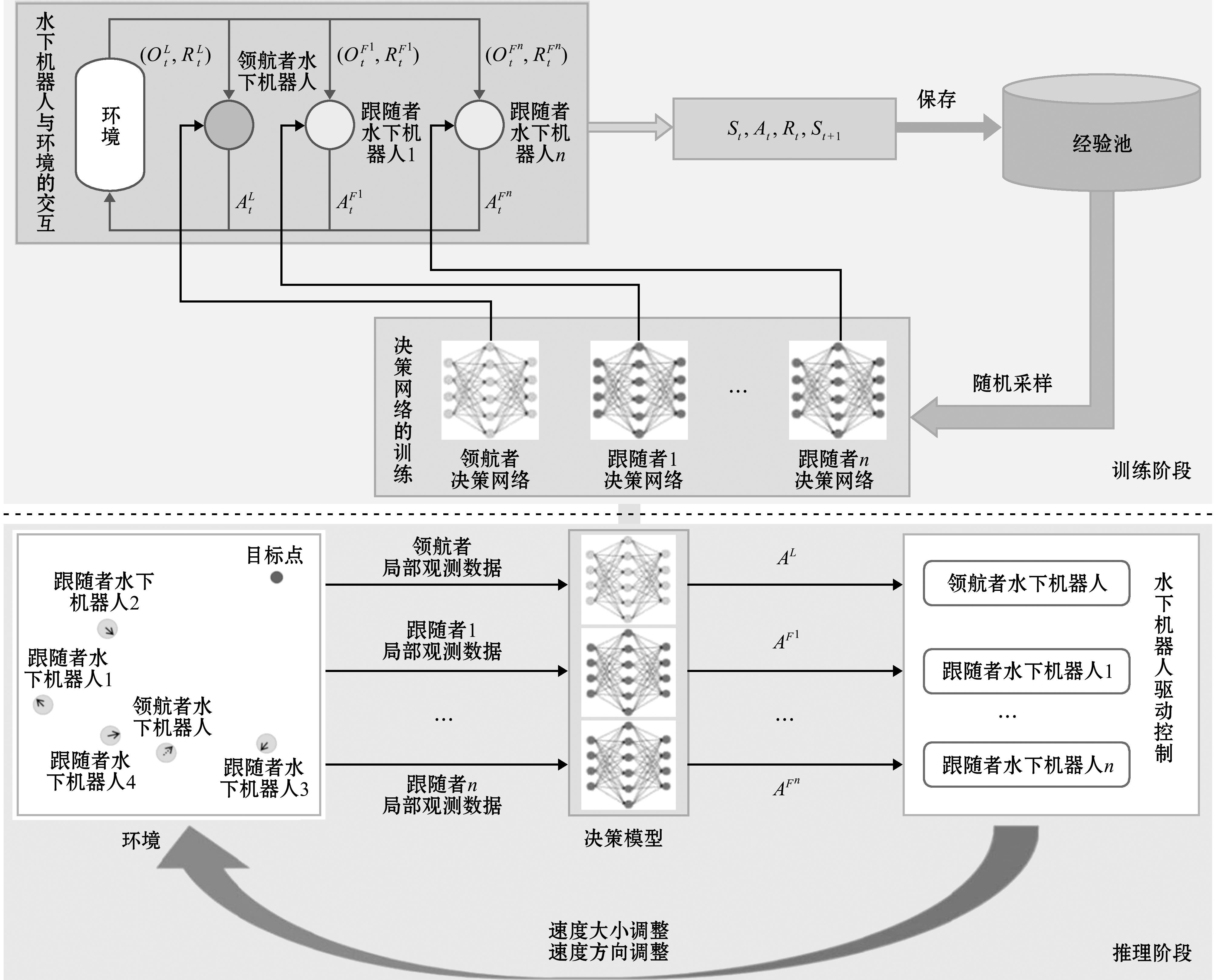
图2 水下机器人运动策略训练与应用总体框架
Fig.2 Overview of motion strategries training and application for underwter robots
在推理阶段，水下机器人群体配备了经过优化的决策模型中的运动控制策略，每一个水下机器人在实际海洋牧场环境中通过与环境的迭代交互，不断根据自身局部观测数据做出合理决策，执行选定的动作并重新获得自身局部观测数据。重复上述过程，以形成编队，并且抵达目标点附近。这种过程确保水下机器人在实际应用中能够协调一致地执行资源评估任务，实现对海洋牧场资源的精确监测和动态评估。
2.2 状态与观测表示
如“2.1节”所述，借助本文的决策模型，每个水下机器人可以根据自身的观测做出相应的控制决策。其中观测描述了每个水下机器人与环境及其他水下机器人的关系。但是，水下机器人的状态表示对于本文所提出的编队控制决策模型的性能也十分重要。水下机器人需要时刻获得自身的相关状态信息，从图1可见，水下机器人i的状态空间表达式为
。
(5)
式中：xi与yi分别表示水下机器人i在全局坐标系下的横纵坐标，
与
分别表示水下机器人i在X轴与Y轴方向上的速度。
由于本文将水下机器人分为两类，且这两类水下机器人的任务分工不同，所以领航者水下机器人与跟随者水下机器人通过自身观测所能得到的信息也有些不同，且所有水下机器人在通过观测获取其他水下机器人相关信息时是无差别的，即未让水下机器人在观测中分辨出此类信息是属于领航者水下机器人还是跟随者水下机器人。为了方便介绍，在此使用了不同的符号来区分领航者水下机器人与跟随者水下机器人。
对于领航者水下机器人来说，其主要任务为带领整个编队抵达目标点附近，所以由其获取目标点的相关信息。领航者水下机器人观测空间可表达为式(6)。
(6)
式中：sL,j(j∈1,2,…,n-1)为其他跟随者水下机器人j相对于领航者水下机器人的相对位置，表示为sL,j=[xj-xL,yj-yL](j∈1,2,…,n-1),sL，G为目标点相对于领航者水下机器人的相对位置，表示为sL,G=[xG-xL,yG-yL]。
对于跟随者水下机器人来说，其主要任务为维持整个编队的形状，以及跟随领航者水下机器人。跟随者水下机器人k的观测空间可表达为式(7)
(7)
式中：sk,i(i∈1,2,…,n-2)为其他跟随者水下机器人i相对于跟随者水下机器人k的相对位置，sk，L为领航者水下机器人相对于跟随者水下机器人的相对位置。
综上所述，在智能体观测空间的设计中，领航者智能体被要求获取到更多的观测信息。通过此种方式简化跟随者智能体所要获取的信息量，以降低跟随者智能体运动策略的学习难度，使其易于学习到最优的运动策略。
2.3 动作表示
如“2.2节”中所述，水下机器人在同一深度运动，而机器人的运动又是靠对其施加力实现，为此本文使用式(8)表达水下机器人i动作空间。
(8)
式中：
与
分别表示水下机器人i在 x和y轴上受到的力，因此水下机器人i的加速度可表达为式(9)。
。
(9)
式中：M为水下机器人的质量。根据式(2)、式(3)，水下机器人即可完成在二维平面内的移动。
2.4 奖励函数的设计
在强化学习中，水下机器人i学习最优控制策略πθ。在每一步t，水下机器人i都观察当前状态St。它使用策略πθ选择一个动作
并获得奖励
然后环境过渡到下一个新状态St+1。每个水下机器人致力于最大化自己的总预期回报，在多水下机器人的编队控制任务问题中，最典型的特征之一就是奖励稀疏。即奖励需要水下机器人通过不断地探索环境及与环境交互才可获得。所以设计一个与该任务相匹配的奖励函数至关重要。
在基于领航者-跟随者的编队控制架构中，该方式最明显的特征为团队中的领航者水下机器人控制的是整个编队的运动趋势，即领航者水下机器人的运动控制策略使其可以带领编队抵达目标点附近。而跟随者水下机器人控制形成编队并维持整个编队的形状，即跟随者水下机器人的运动控制策略使其在维持编队的情况下跟随领航者水下机器人。由此，设计的奖励函数如下所示。
Rtotal=RL+n×RF，
(10)
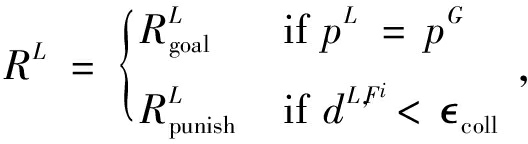
(11)
(12)
式中：式(10)为本文任务的总奖励函数，n为跟随者水下机器人的数量；式(11)表示领航者水下机器人的奖励函数；式(12)表示跟随者水下机器人的奖励函数。在式(11)中，pL为领航者水下机器人的位置，pG为其所要抵达的目标点的位置，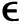
coll为碰撞阈值。在式(12)中，
为跟随者水下机器人维持编队所得到的奖励，称之为“编队奖励
为跟随者水下机器人向领航者水下机器人移动的同时与其保持一定距离所得到的奖励，称之为“跟随编队奖励
为跟随者水下机器人所形成的编队质心与领航者水下机器人保持一定距离所得到的奖励，称之为“质心跟随奖励
为跟随者水下机器人与其他水下机器人发生碰撞后所得到的惩罚。ka，kb，kc分别为这3种奖励的权重，kd为碰撞惩罚的权重。
2.5 基于MADDPG的水下机器人运动策略学习
2.5.1 MADDPG算法介绍 MADDPG算法[23]是DDPG(深度确定性策略梯度)算法在多水下机器人环境中的变体，采用CTDE(集中式训练，分布式执行)范式。所谓CTDE指的是在训练过程中，每个水下机器人不仅要考虑自己的状态、观测等信息，也要将其他水下机器人的相关信息考虑在内。通过此种做法每个水下机器人在每一个时间步的过程中都将得到一个更准确的Q值来引导自身策略的学习。当训练完成后，每个水下机器人在执行任务过程中，仅根据自身的局部观测信息来选取动作，这时就不需要再考虑环境内其他水下机器人的任何相关信息。通过这种范式的应用，减少了多水下机器人环境设置中的非平稳性问题，这种做法极大地稳定了多个水下机器人同时学习的情况。在MADDPG算法中，每个水下机器人采用的是确定性策略，即从水下机器人的当前状态直接输出一个确定的执行动作，而不是输出一个动作的概率分布。因此该方法可用于连续动作控制。
从图3可见，MADDPG算法中每一个水下机器人都有一个自己的Actor-Critic网络架构。在多水下机器人环境设定中，本文将由n个水下机器人组成的状态集合定义为X=(s1，s2，…，sn)；动作集合为A=(a1，a2，…，an)；奖励集合为R=(r1，r2，…，rn)。每一个水下机器人的Actor当前网络μ根据这一时刻的状态si输出一个策略，生成当前动作
其Critic当前网络Q基于所有水下机器人的状态和动作估计一个集中的动作值函数
和θQ为Actor当前网络和Critic当前网络的对应参数。在水下机器人的每次交互中，水下机器人将相关学习内容存储在经验池中。此外为了稳定训练，构建了两个目标网络，分别为Actor目标网络μ′与Critic目标网络Q′。对于任意的一个水下机器人i，Critic当前网络根据公式(13)更新。
(13)
(14)
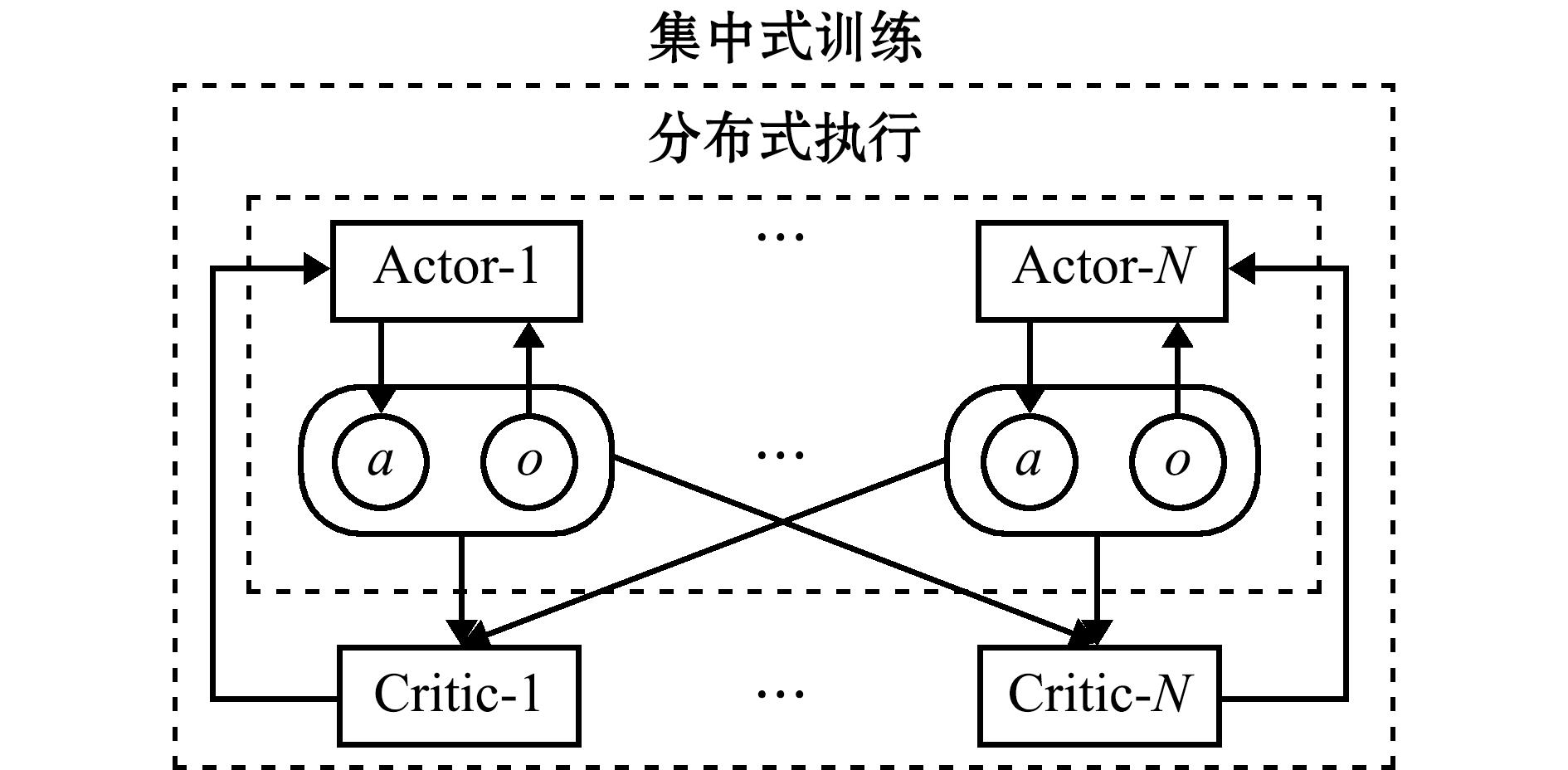
图3 MADDPG算法网络结构
Fig.3 Network architecture of MADDPG algorithm
式中：L(θi)为水下机器人i的Critic当前网络的损失函数，公式(14)中ri为水下机器人在当前状态下所获得的即时奖励，
部分表示未来奖励的期望值用于估算从下一状态开始的未来累积回报，yi为水下机器人i的目标Q值，用于更新Critic网络时用作“真实”Q值的估计，使得Critic网络通过最小化损失函数来逼近目标Q值。同时，Actor当前网络通过公式(15)进行优化。
。
(15)
目标网络的网络参数使用soft-update(软更新)的方式定期从当前网络进行复制，如公式(16)所示。
(16)
MADDPG算法为每一个水下机器人都创建了一个Actor-Critic网络架构，因此在训练完成的同时得到领航者水下机器人与跟随者水下机器人的运动控制策略。这不仅减少了训练成本，而且缓解了多水下机器人学习过程中的环境非平稳性问题。
2.5.2 水下机器人决策网络设计 MADDPG算法遵循Actor-Critic方法的框架，因此当使用该算法对水下机器人进行训练时，每个水下机器人的决策网络由两部分组成，分别为Actor网络与Critic网络。这两个网络均通过深度神经网络进行拟合，网络内部结构完全相同，但是网络的输入与输出是不同的。具体的网络结构如图4所示。
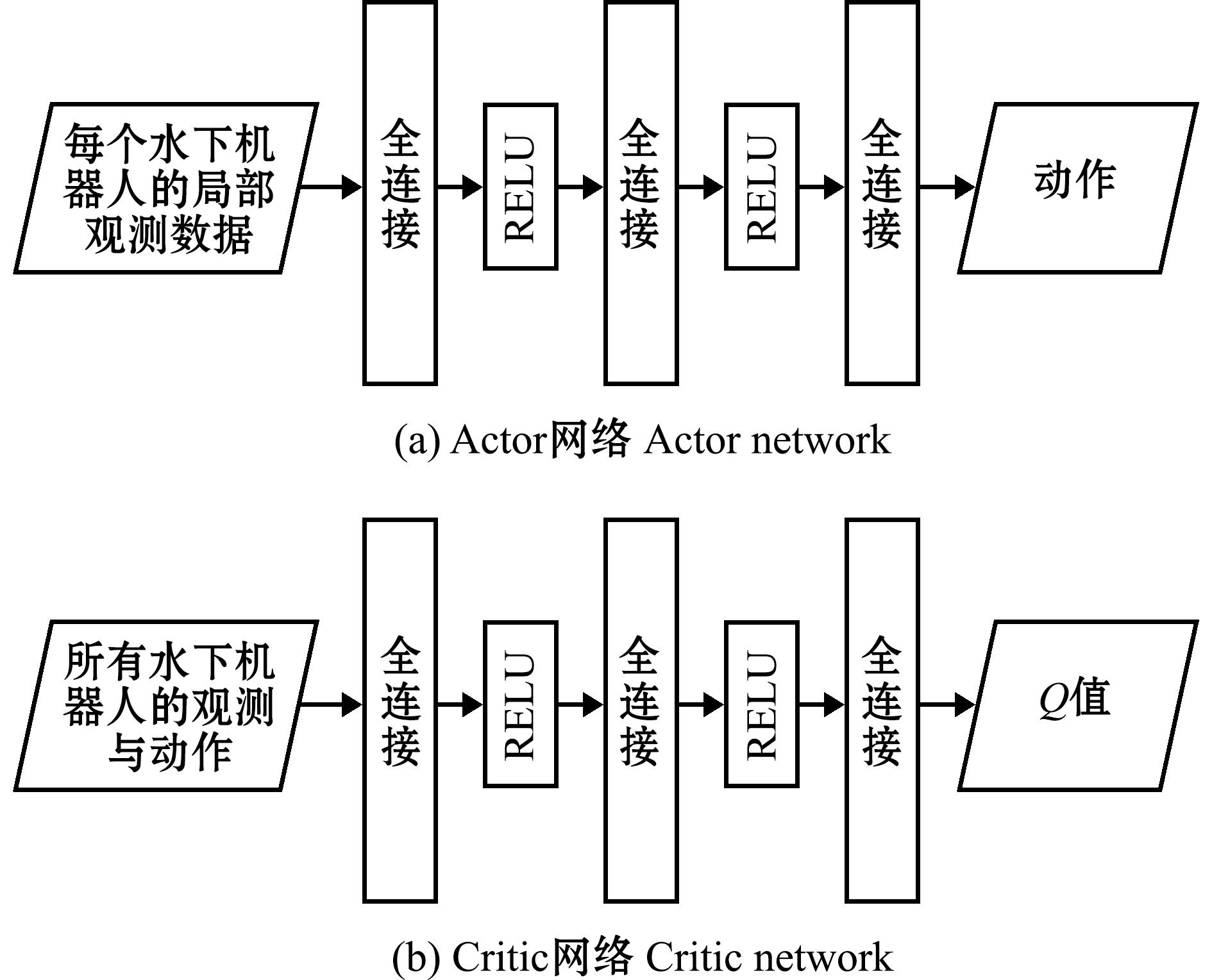
图4 网络结构
Fig.4 Network architecture
Actor网络的输入执行海洋资源评估任务时水下机器人获取的局部观测信息，通过3个全连接层后输出一个动作。在该网络中前两个全连接层使用RELU激活函数，最后一个全连接层不使用激活函数。Critic网络的输入与Actor网络相同，包含观测和动作信息，通过3个全连接层后输出该智能体所做出动作的价值。在该网络中前两个全连接层使用RELU激活函数，最后一个全连接层不使用激活函数。
由“2.5.1节”所述，MADDPG算法具有额外的目标网络，Actor网络和Critic网络分别有一个结构完全相同的目标网络。目标网络的参数是从当前网络通过软更新的方式进行一定程度的复制得到的，以确保算法在复杂任务下的策略稳定性和收敛性。通过这种做法可以使得目标值的计算不再依赖当前的估计值，以达到稳定训练的目的。由于目标网络的结构与其所对应的网络结构一致，因此并未在图4中画出。
2.5.3 算法流程 融合领航者-跟随者架构与MADDPG的多水下机器人编队控制方法的算法流程见表1。
表1 基于MADDPG算法的多水下机器人编队控制方法伪代码
Tab.1 Pseudocode for multi-underwater robot formation control method based on the MADDPG algorithm
算法1 基于MADDPG算法的多水下机器人编队控制方法algorithm1 multi-underwaterrobotformationcontrolmethodbasedontheMADDPGalgorithm1.随意初始化每个水下机器人Actor-Critic当前网络及目标网络的所有参数,清空经验池D。设置训练回合数M,环境内水下机器人的数量N以及每个回合内水下机器人所能执行的时间步T;2.forepisodeinrange(M);3.环境初始化,并初始化所有水下机器人的无碰撞状态X=(s1,s2,…,sn);4.初始化随机噪声 用于探索环境;5.fortinrange(T);6.每个水下机器人根据当前的策略和探索噪声执行动作ai=μθμ(oi)+ ;7.所有水下机器人执行动作(a1,a2,…,an)后得到及时奖励R,以及下一时刻的状态X′;8.将所有水下机器人通过交互所得到的所有数据(X,A,R,X′)存入经验池D中;9.对于每一个水下机器人i:10.从经验池D中,通过随机采样的方式得到S个小批量样本(X,A,R,X′);11.根据公式(14)计算出目标Q值;12.根据公式(13)更新Critic网络参数;13.根据公式(15)更新Actor网络参数;14.endfor;15.根据公式(16)更新两个目标网络参数;16.endfor;17.endfor
该方法使用随机权重初始化每个水下机器人Actor-Critic当前网络及目标网络的所有参数。在每个训练回合初始时随机生成所有水下机器人与目标点的位置，并且初始化随机噪声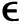。在每个时间步，算法都会执行以下操作。首先，水下机器人将收到它们的局部观察信息。接下来，每个水下机器人根据当前的策略和探索噪声执行动作ai=μθμ(oi)+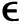。然后，环境同时执行水下机器人的动作并生成交互数据(当前观察、当前动作、新观察和奖励)，这些数据被保存到经验池中。最后，根据公式(14)计算出目标Q值，使用Adam优化器更新每一个水下机器人的Critic当前网络与Actor当前网络，并使用软更新方式来更新目标网络。
在此过程中，为了避免水下机器人在训练过程中对特定环境的过拟合，将所有机器人和目标点随机分布在初始状态下。同时，为防止随机设定初始位置时出现机器人位置重叠或碰撞的情况，在训练过程中每个回合起始，使用了一种碰撞检测措施，确保在训练前水下机器人初始位置不重叠，并避免彼此过于接近。
3 仿真验证与性能分析
3.1 实验环境与参数设置
实验在Ubuntu18.04系统上使用gym模块进行，该系统具有Intel i5-10200H CPU、GeForce1650Ti图形卡和16G RAM。本文的多水下机器人编队控制实验环境如图5所示的海域中。环境中包含5个水下机器人，其中一个为领航者水下机器人，4个为跟随者水下机器人。除水下机器人外，还设有一个地标，称为目标点。这些水下机器人的主要任务是协同编队完成海洋资源评估任务，在该任务中，领航者水下机器人的目标是到达地标，因此任务开始时，领航者首先获得目标点的相对位置信息并朝目标点移动。同时，跟随者水下机器人的目标是保持合理的编队并跟随领航者，它们通过监测领航者的位置和运动方向，调整自身位置以确保队形的协调。训练中，每一回合开始时通过随机分布水下机器人和地标的初始位置(即坐标)来增加任务多样性。通过这种随机初始化，水下机器人逐渐学习到更为稳健的编队策略，使其能够在不同环境中有效完成领航者到达地标、跟随者保持编队的任务。
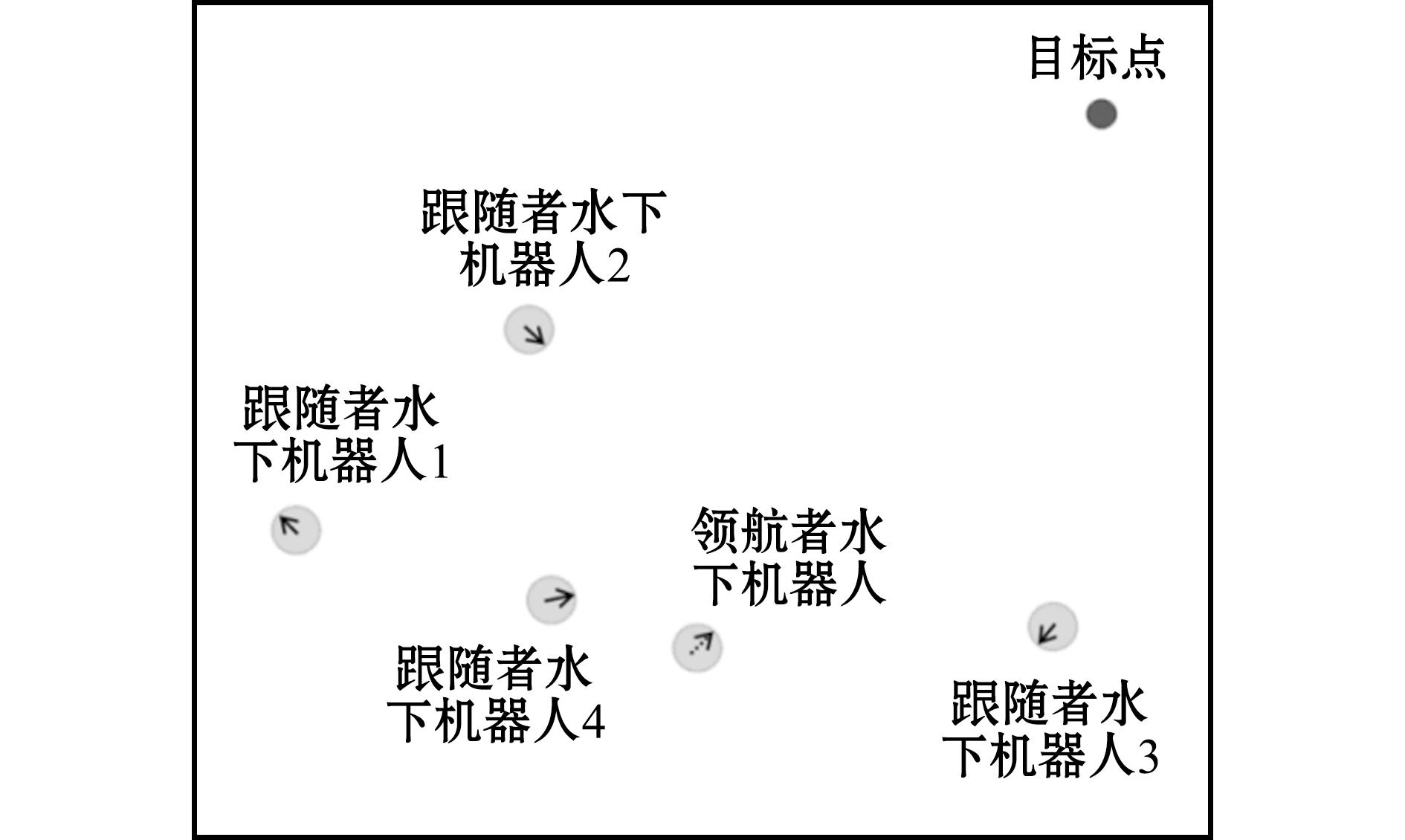
图5 实验环境
Fig.5 Experimental environment
本文使用学习率为0.01的Adam优化器更新目标网络。γ设置为0.95；水下机器人间碰撞距离为0.1；最大回合长度设为150；经验池大小为106，当每100个样本添加到经验池后更新网络参数。随机在经验池中挑选1 024个小批量样本用于更新网络，实验共进行60 000个回合训练。
3.2 有效性验证
在训练过程中，利用水下机器人在一个回合内获得的总奖励来评估编队控制策略的成功。从图6可见，随着训练的进行，水下机器人在每个回合中所获得的总奖励逐渐增加。具体来说，水下机器人在一个回合内所获得的总奖励值从-10 000逐渐升高，且稳定在21 000左右。这表明水下机器人所学习的编队控制策略性能有所提高，其群体学习过程逐渐收敛。图6中的插图是水下机器人在训练不同阶段所表现出的学习效果图，这些插图发生在相应回合数中的最后几个时间步。从插图可以看出，在训练初期水下机器人获得较低的奖励，习得的策略使得群体的分布较为分散，无法形成有效的编队；而在训练后期，习得的策略能够让水下机器人群体既可以抵达目标点附近，又在目标点周围形成了稳定的编队形状。这表明通过本文所提出的方法，水下机器人最终可得到稳定的编队控制策略。
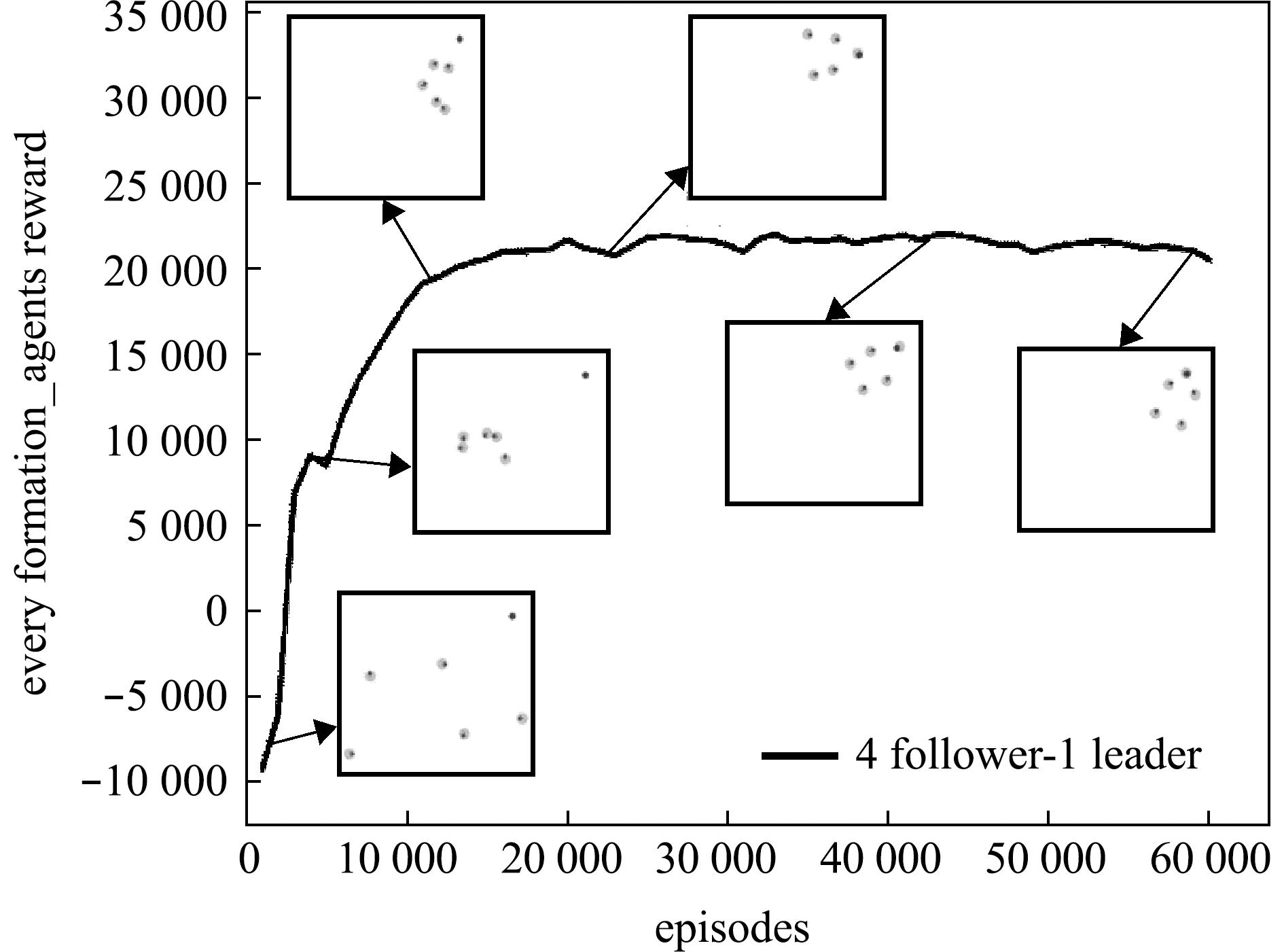
图6 训练时期水下机器人在每个回合内所获得的总奖励曲线
Fig.6 Total reward curve obtained by underwater robots in each episode during training
为了验证水下机器人所习得编队控制策略的有效性，以及使用本文方法是否可以得到实现编队控制的决策模型。本文选择通过可视化测试阶段(即“2.1节”中所述的推理阶段)水下机器人群体的轨迹图来进行评估。在实验开始前，初始条件设定为目标点在地图的右上角；领航者水下机器人在地图的左下角；4个跟随者水下机器人随机初始化在环境中的任意一点。期望领航者水下机器人能够带领4个跟随者水下机器人以编队的形式抵达目标点附近，所以设定当这4个跟随者水下机器人与领航者水下机器人形成编队之后，领航者水下机器人再带领整个编队进行单目标追踪移动。5个水下机器人在160个时间步中的轨迹如图7所示。从图7可见，环境中的水下机器人从最初无序分布，自主地形成了一个编队形状。并且领航者水下机器人在编队形成之后可以带领整个编队抵达目标点附近，即4个跟随者水下机器人在与领航者水下机器人形成编队后，会以编队的形式跟随领航者水下机器人进行移动。这表明水下机器人所学习到的运动策略可以产生稳定的编队控制。说明使用本方法可以得到用于实现编队控制的决策模型，实验验证了本方法的有效性。
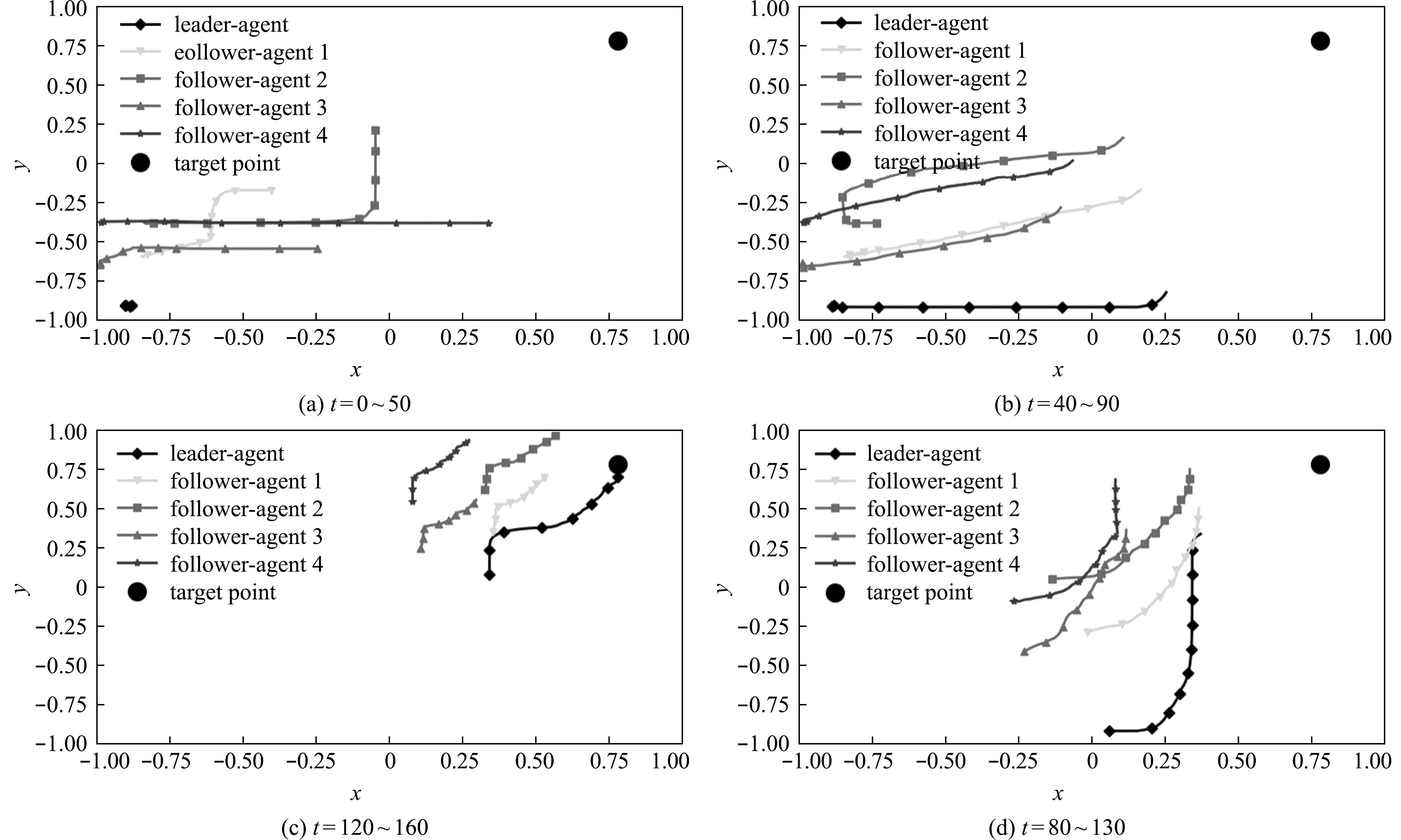
图7 测试时期水下机器人群体在执行任务时的轨迹
Fig.7 Trajectory of the underwater robot swarm during task execution in the testing phase
3.3 性能对比
为了验证本文算法的性能，将本文算法与用于编队的DDPG[23]、ADDPG[20]等较为经典强化学习算法进行了对比。
当群体规模大小为5时，使用这3种算法所训练的跟随者水下机器人在每个回合下获得的总奖励曲线如图8所示。从图8可见，训练初期3种算法的奖励曲线均在快速上升；大约在11 000回合后本文所使用的MADDPG算法获取的奖励逐渐趋于稳定且达到收敛，DDPG的奖励曲线大约在45 000回合后才逐渐到达收敛，而ADDPG的奖励曲线上升至6 000回合之后呈现下降趋势并最终趋于稳定。MADDPG算法和DDPG算法都使得水下机器人群体学习到了稳定的编队控制策略，且MADDPG算法相比较于DDPG算法收敛速度更快且所获取的奖励值也更高。而ADDPG算法无法在本文所设定的任务中学习到稳定的编队控制策略，猜测这是由于本文任务中的奖励稀疏，ADDPG算法通过“2.4节”中所设计的奖励函数无法正确引导水下机器人策略的学习。这表明本文算法能够在奖励稀疏的情况下更快让水下机器人获得成功的经验，并且可让水下机器人策略学习的速率更快。从最终的总奖励收敛值上来说，本文算法相比较于其他两种算法可收敛到更高的数值。这表明本文算法拥有更好的训练效果，体现出其先进性。
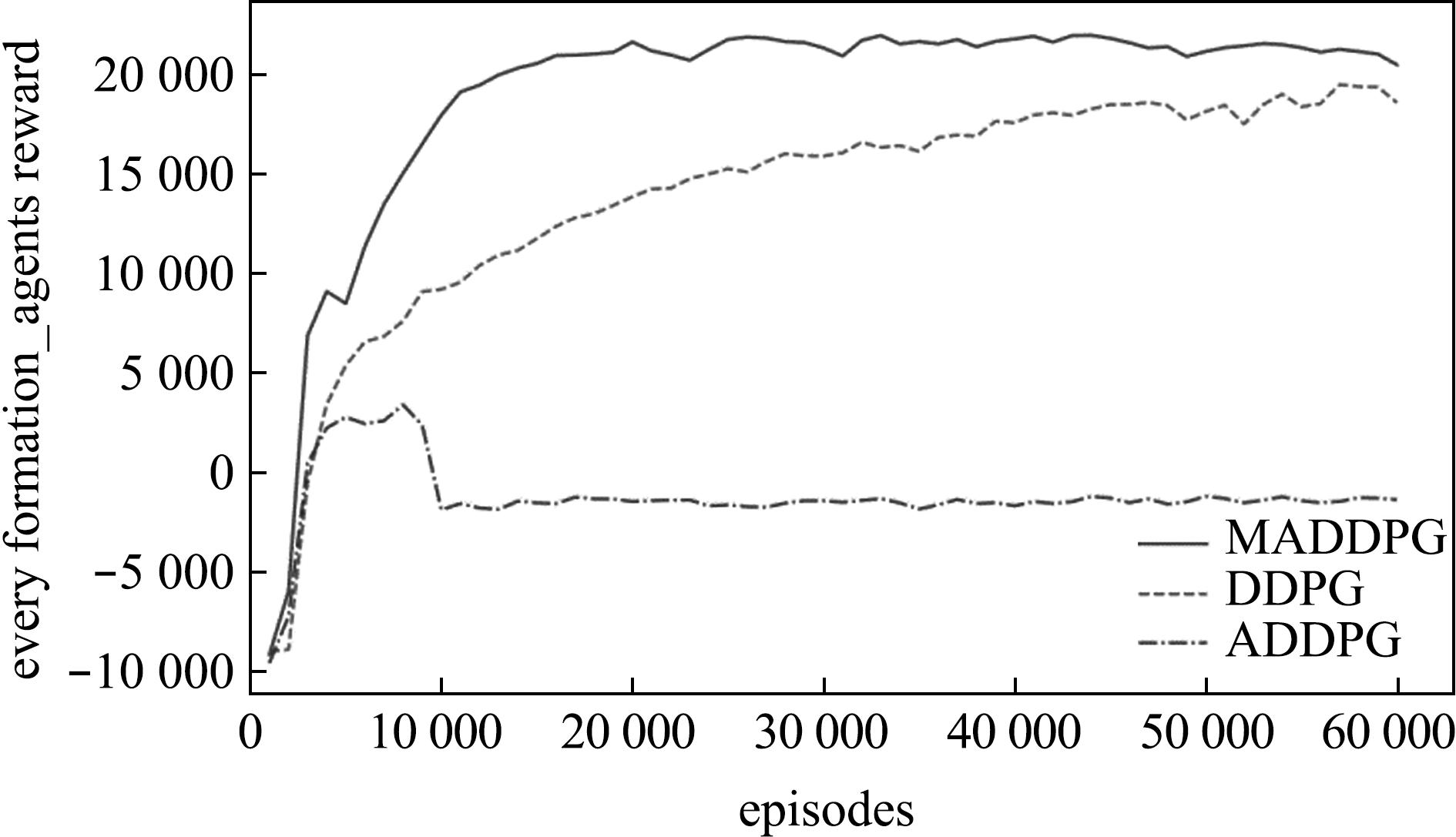
图8 训练时期3种算法的水下机器人总奖励对比曲线
Fig.8 Comparative total reward curves of underwater robots for three algorithms during training
为了评估水下机器人群体所习得的编队控制策略的性能，使用其在测试期间执行任务时彼此之间的距离误差来进行评判。在该评估任务中所有水下机器人与目标点都随机初始化在环境中的任一位置。并且当整个编队抵达目标点附近后，目标点重新刷新在环境中的任一位置。以此来使得环境中的水下机器人以更多的步骤进行移动。MADDPG算法中5个水下机器人彼此之间的距离误差如图9所示，DDPG算法中5个水下机器人彼此之间的距离误差如图10所示。
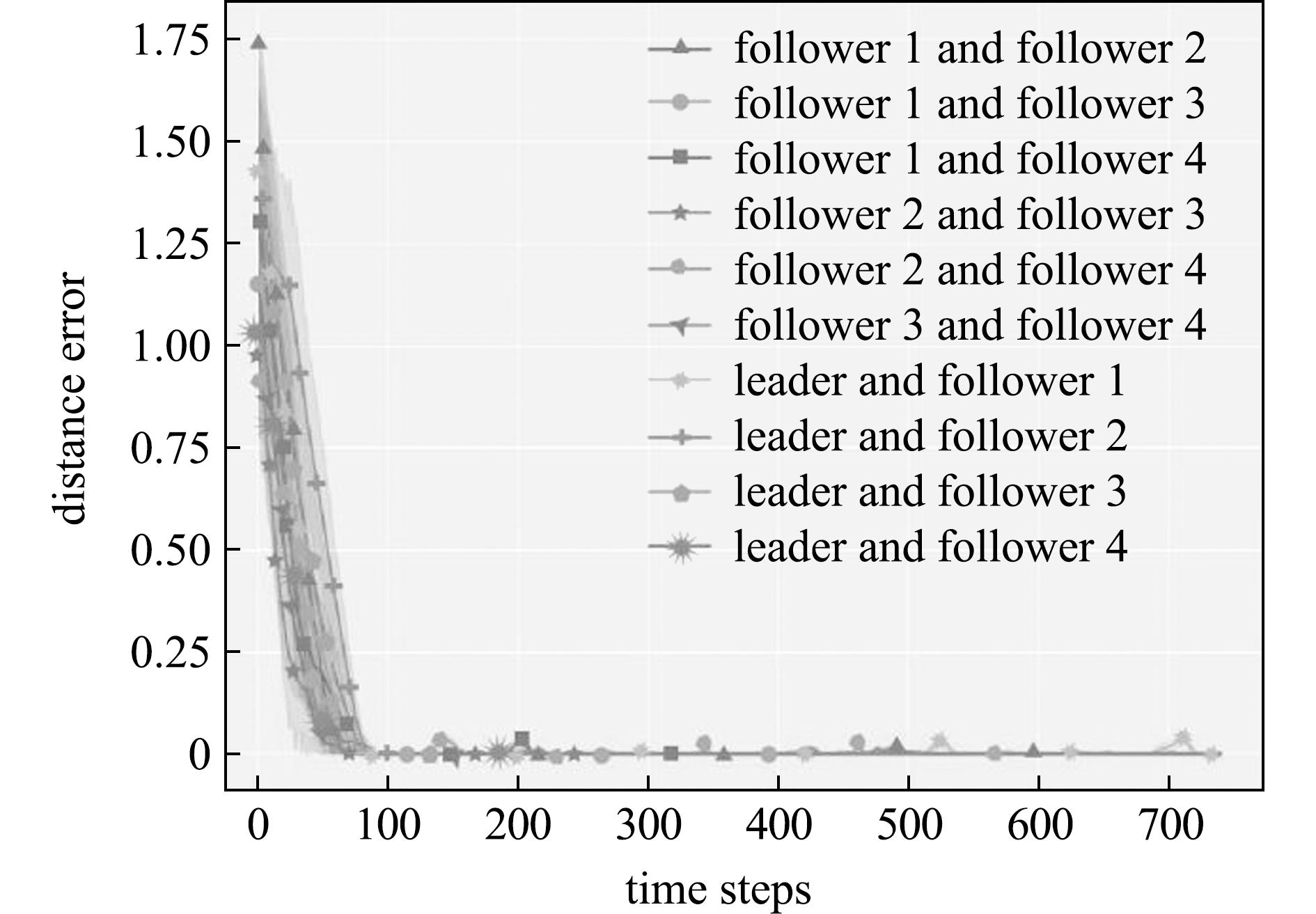
图9 MADDPG算法在测试时期水下机器人执行任务时彼此之间的距离误差
Fig.9 Distance errors between underwater robots during task execution in the testing phase using the MADDPG algorithm
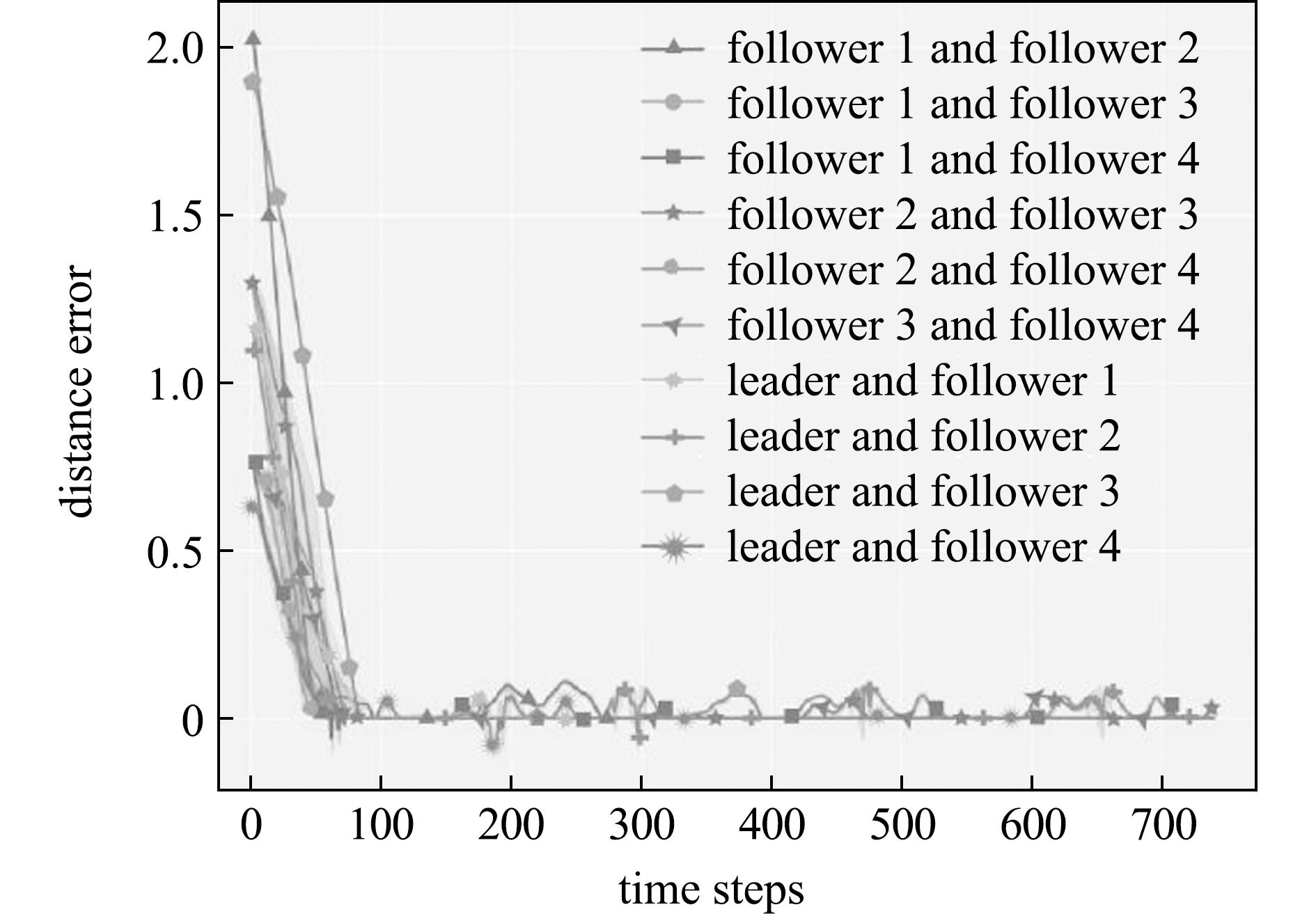
图10 DDPG算法在测试时期水下机器人执行任务时彼此之间的距离误差
Fig.10 Distance errors between underwater robots during task execution in the testing phase using the DDPG algorithm
在执行任务时，水下机器人彼此之间的距离与期望其所保持的距离间的差值定义为距离误差，误差为负值时表示为水下机器人发生碰撞。以此为标准时，从图9可见，MADDPG算法在时间步骤为90时，水下机器人之间的距离误差趋于0。这表明该时刻水下机器人群体已形成编队。此外，该时刻之后的距离误差曲线再无较大波动。这表明水下机器人群体在执行任务时保持了稳定的编队队形。从图10可见，DDPG算法在时间步骤为110时，水下机器人之间的距离误差趋于0，但该时刻之后距离曲线存在较大波动。这表明通过这两种算法所习得的编队控制策略都能较好地完成本文任务，但通过MADDPG算法所习得的编队控制策略能够使得水下机器人群体更快地集结成编队，且可以保持稳定的编队队形。而水下机器人配备通过DDPG算法所习得的编队控制策略时，群体更容易发生队形分离或碰撞。本文所设计的奖励函数成功引导了水下机器人的编队控制策略学习，通过MADDPG算法所习得的编队控制策略相较于DDPG算法拥有更优的性能。
4 讨论
4.1 附加实验设计
为进一步验证本文提出的基于多智能体深度确定性策略梯度(MADDPG)算法的多水下机器人编队控制方法在不同群体规模下的适应性与泛化能力，本文设计了一组附加实验，通过增加环境中的跟随者水下机器人数量，来测试该方法在不同规模群体中的表现。在这些附加实验中，为了消除群体规模变化对奖励分布的影响，调整了奖励函数中的权重系数。具体而言，调整后的奖励函数确保水下机器人在任何规模的群体中，在每个时间步中获得的最大奖励值保持一致。通过这种调整，无论水下机器人数量如何变化，整个回合内的最大奖励都能够达到相同的标准，这意味着水下机器人在一个回合内所能获得的最大总奖励的收敛值不会受到群体规模变化的干扰。
这种奖励函数的设计有效消除了群体规模变化所带来的潜在偏差，为不同群体规模下的学习性能提供了一个公平的对比基础。通过这种设置，能够确保每个群体规模在学习过程中面临的挑战相对一致，从而能够深入分析群体规模对编队控制策略学习效果的影响。
4.2 结果分析
在附加实验中，笔者测试了水下机器人群体规模为6、7、8、9和10时的表现，并记录了每个回合的总奖励值变化曲线，实验结果如图11所示。从图11可见，不同群体规模下的奖励曲线均从初始的-10 000左右开始，经过一定的训练阶段后逐步上升，最终趋于稳定。这表明，所提方法能够在不同规模的水下机器人群体中学习到稳定的编队控制策略。奖励曲线的逐步上升与最终的稳定性，验证了该方法在多机器人协作环境中的良好收敛性与学习稳定性。
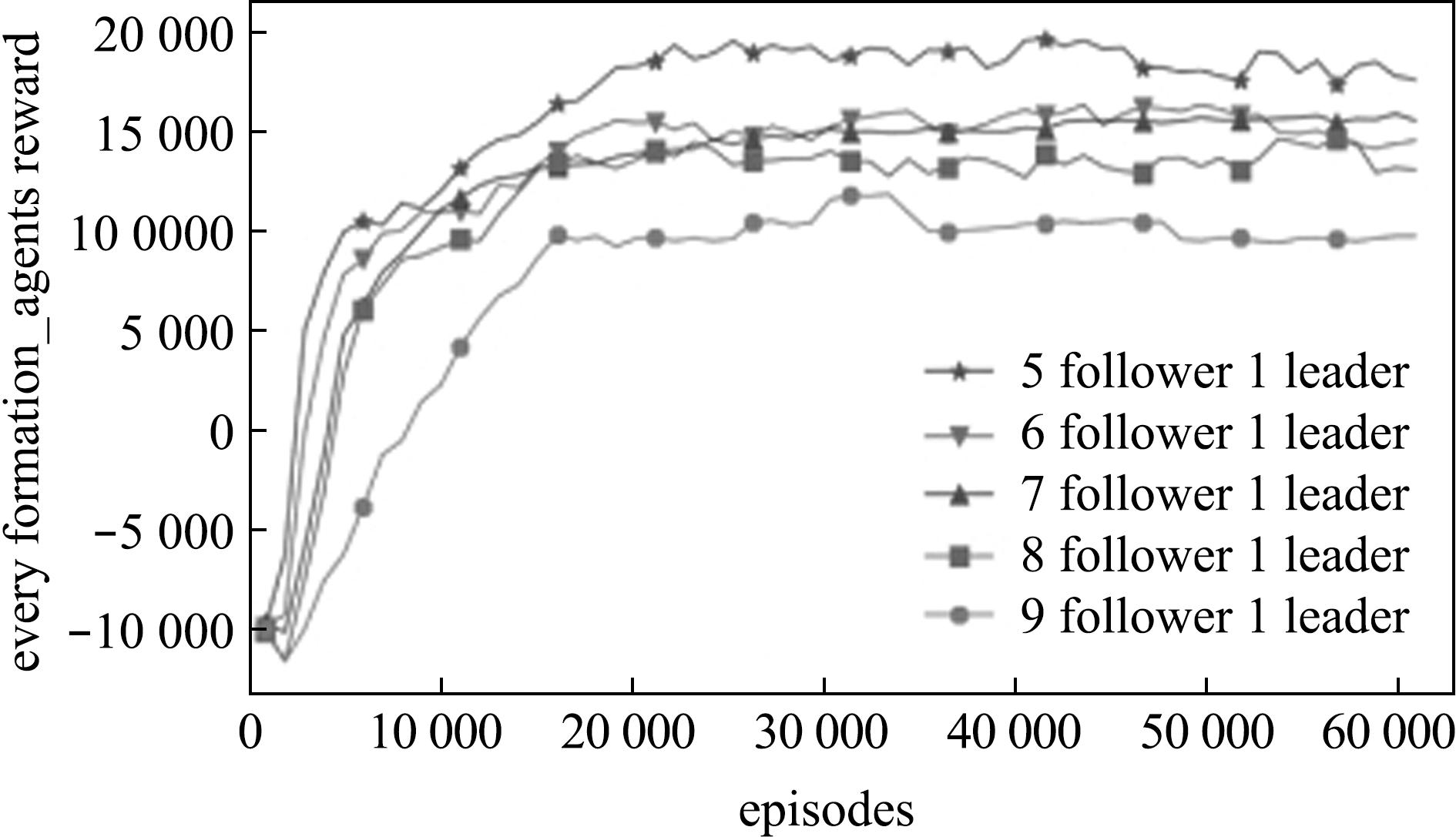
图11 训练不同群体规模时的总奖励曲线
Fig.11 Total reward curves for training with different swarm sizes
尽管所有群体规模的奖励曲线最终趋于稳定，但不同规模的最大收敛值存在显著性差异。具体来说，当群体规模为6时，水下机器人最终在一个回合内获得的总奖励值约为20 000；当群体规模为7、8、9时，奖励值稳定在14 000左右；而当群体规模增至10时，总奖励的最大收敛值则降至约9 800。这一现象表明，群体规模的增大对奖励收敛值产生了影响，随着规模的增加，总奖励值呈现下降趋势。该趋势可能是由于更大群体中机器人之间的交互与协调变得更加复杂，从而影响了整体任务的执行效率。
随着群体规模的增大，总奖励值出现递减趋势，主要原因在于机器人数量增多后，个体之间的碰撞概率也随之上升。碰撞行为通常会带来负奖励，这会抑制整体奖励的增长。在群体规模较大的情况下，机器人之间的空间约束和协调需求增多，碰撞发生的概率和频率也随之提高，从而导致负奖励的累计效应增强，进而影响总奖励的收敛值。因此，群体规模的增大导致了奖励值的下降，这反映了多机器人编队控制中，随着个体数量增加，碰撞管理和资源协调的复杂性显著提升。
5 结论
1)基于多智能体深度确定性策略梯度(MADDPG)算法的多水下机器人编队控制方法生成的编队策略展现出类似生物集群运动模式的多样化特性，显著提升了水下机器人群体对资源的覆盖率和评估精度。
2)在资源分布动态变化的场景中，该方法能够快速适应变化需求，生成灵活的集群编队策略。
3)与传统控制理论方法相比，本方法无须预设具体模型信息，避免了模型依赖性。在奖励稀疏问题下，展现了更高的学习效率和更优的学习效果。
[1] 陈勇.中国现代化海洋牧场的研究与建设[J].大连海洋大学学报,2020,35(2):147-154.CHEN Y.Research and construction of modern marine ranching in China:a review[J].Journal of Dalian Ocean University,2020,35(2):147-154.(in Chinese)
[2] 杨红生,章守宇,张秀梅,等.中国现代化海洋牧场建设的战略思考[J].水产学报,2019,43(4):1255-1262.YANG H S,ZHANG S Y,ZHANG X M,et al.Strategic thinking on the construction of modern marine ranching in China[J].Journal of Fisheries of China,2019,43(4):1255-1262.(in Chinese)
[3] 鲁红月,张畅,陈新军.基于环境因子的渔业资源评估研究进展[J].海洋湖沼通报,2024,46(1):191-199.LU H Y,ZHANG C,CHEN X J.Progresses of environmental factor basing fishy stock assessments[J].Transactions of Oceanology and Limnology,2024,46(1):191-199.(in Chinese)
[4] WANG Z W,YAO L J,YU J,et al.Evaluation ofthe ecological carrying capacity of Wailingding marine ranching in Zhuhai,China by high-resolution remote sensing[J].Frontiers in Marine Science,2024,11:1354407.
[5] 吴一尘,刘天宇,王营.基于领航者-跟随者技术的多机器人编队控制[J].南方农机,2021,52(19):30-32.WU Y C,LIU T Y,WANG Y.Multi robot formation control based on leader follower technology[J].China Southern Agricultural Machinery,2021,52(19):30-32.(in Chinese)
[6] 王艺凯,孙俊,王偲.欠驱动无人艇集群协同编队路径规划仿真[J].计算机仿真,2023,40(6):485-490.WANG Y K,SUN J,WANG S.Simulation of path planning for under-driven unmanned surface vehicle cluster cooperative formation[J].Computer Simulation,2023,40(6):485-490.(in Chinese)
[7] 李科宇,杨尚志,张刚,等.基于改进人工势场法的多智能体编队避障[J].控制工程,2024,31(1):168-177.LI K Y,YANG S Z,ZHANG G,et al.Multi-agent formation obstacle avoidance based on improved artificial potential field method[J].China Industrial Economics,2024,31(1):168-177.(in Chinese)
[8] LI J H,KANG H,KIM M G,et al.Adaptive formation control of multiple underactuated autonomous underwater vehicles[J].Journal of Marine Science and Engineering,2022,10(9):1233.
[9] SONG Z L,WU Z Y,HUANG H C.Cooperative learning formation control of multiple autonomous underwater vehicles with prescribed performance based on position estimation[J].Ocean Engineering,2023,280:114635.
[10] 孙栋,汤奇荣,刘明昊,等.面向模块化设计的水下机器人集群编队控制[J].舰船科学技术,2024,46(2):68-73.SUN D,TANG Q R,LIU M H,et al.Research on swarm formation control of modular underwater robots[J].Ship Science and Technology,2024,46(2):68-73.(in Chinese)
[11] 朱大奇,庞文,任科蒙.多AUV水下协作搜索研究现状与展望[J].上海理工大学学报,2022,44(5):417-428.ZHU D Q,PANG W,REN K M.Research status and prospect of multi-autonomous underwater vehicle cooperative search control[J].Journal of University of Shanghai for Science and Technology,2022,44(5):417-428.(in Chinese)
[12] ZHANG T,YANG Z,LI Y.Multi-agent deep reinforcement learning for underwater target search and tracking[J].Journal of Marine Science and Engineering,2023,11(1):85.
[13] 董豪,杨静,李少波,等.基于深度强化学习的机器人运动控制研究进展[J].控制与决策,2022,37(2):278-292.DONG H,YANG J,LI S B,et al.Research progress of robot motion control based on deep reinforcement learning[J].Control and Decision,2022,37(2):278-292.(in Chinese)
[14] ZHAO X,ZHANG H.Autonomous underwater vehicles for marine resource assessment:a review[J].Marine Technology Society Journal,2023,57(2):54-63.
[15] CHEN L,SUN Y.Multi-agent reinforcement learning for cooperative underwater exploration and monitoring[J].Applied Ocean Research,2022,125:103248.
[16] KNOPP M,AYKIN C,FELDMAIER J,et al.Formation control using GQ(λ) reinforcement learning[C]//2017 26th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN).Lisbon,Portugal.IEEE,2017:1043-1048.
[17] WANG J,LIU Y.Collaborative control of multiple AUVs for marine ranching monitoring[J].Ocean Engineering,2023,250:110999.
[18] 赵启,甄子洋,龚华军,等.基于D3QN的无人机编队控制技术[J].北京航空航天大学学报,2023,49(8):2137-2146.ZHAO Q,ZHEN Z Y,GONG H J,et al.UAV formation control based on dueling double DQN[J].Journal of Beijing University of Aeronautics and Astronautics,2023,49(8):2137-2146.(in Chinese)
[19] ZHAO Y J,MA Y,HU S L.USV formation and path-followingcontrol via deep reinforcement learning with random braking[J].IEEE Transactions on Neural Networks and Learning Systems,2021,32(12):5468-5478.
[20] XIE J J,ZHOU R,LIU Y,et al.Reinforcement-learning-based asynchronous formationcontrol scheme for multiple unmanned surface vehicles[J].Applied Sciences,2021,11(2):546.
[21] PARK M,SHIN J,YANG I.Anderson acceleration for partially observable Markov decision processes:a maximum entropy approach[J].Automatica,2024,163:111557.
[22] LI B,GAN Z G,CHEN D Q,et al.UAV maneuvering target tracking in uncertain environments based on deep reinforcement learning and meta-learning[J].Remote Sensing,2020,12(22):3789.
[23] XU Z,LYU Y,PAN Q,et al.Multi-vehicle flocking control with deep deterministic policy gradient method[C]//2018 IEEE 14th International Conference on Control and Automation (ICCA).Anchorage,AK,USA.IEEE,2018:306-311.