近年来,随着中国社会经济的不断发展,居民生活水平不断提高,肉质鲜美、蛋白质含量高且低脂的水产品需求量稳步上涨。与此同时,消费者的食品安全意识也在不断提升。由于冰鲜水产品的高度易腐特性,在其配送过程中,当配送时间超出客户心理预期时,势必引起客户对水产品品质的质疑,从而影响企业的客户满意度。目前,冰鲜水产品配送企业仍存在配送成本高、客户满意度低等营销短板,因此,构建高效率的水产品配送调度方案迫在眉睫。
水产品配送过程中,由于品种繁多,配送温度需求也呈现多层次化。通常按温度区间把水产品分为冷冻水产品(-18 ℃~-10 ℃)、冰鲜水产品(-2 ℃~2 ℃)和常温水产品(20 ℃~25 ℃)3种状态,在水产品需维持低温状态时,水产品的包装一般采用冰袋配合聚乙烯泡沫箱实现基础保冷。考虑到实际配送过程中的客户满意度及配送成本等因素,黄益平等[1]在前景理论中结合客户的个人偏好,构建了引入模糊理论的客户满意度函数。刘虹等[2]基于受现实因素影响导致的配送时间不确定性,构造了结合前景理论的时间窗服务价值函数。Ganji等[3]和于江霞等[4]对顾客进行分类,以提高对优质客户的服务质量。Yamada等[5]基于客户满意度及准时配送,建立了一个考虑取件时间及变量参数影响的取件调度模型。Wang等[6]提出产品的新鲜程度和交付的及时性是影响易腐品最终交付客户满意度的两个关键因素。王勇等[7]和李畅等[8]针对生鲜品时效要求强、温度要求高的特点构建了多目标优化模型。在联合装载及配送问题研究中,Kurpel等[9]考虑了摆放方向、负载稳定性等实际约束条件,以最大化集装箱装载价值或最小化集装箱数量为目标,求解了多个集装箱的装载问题。Mahvash等[10]在货箱摆放方向无限制的条件下,增加了装箱因子,提高了货箱装箱率。Dornas等[11]综合考虑不同尺寸货箱可旋转的摆放位置及对剩余空间的充分利用,提出对三维装箱问题的求解方案。雷定猷等[12]和高梦伟等[13]引入车辆的装载约束,在其他现实约束基础上,构建了平衡装载约束下的车辆路径问题模型。Castellucci等[14]通过联合集装箱的实际到达时间和卡车离开时间的集装箱装载问题,建立了一个量化延误对运力利用及卡车出发时间影响的模型。对于传统启发式算法存在的缺陷问题,董凌艳等[15]和周卫标等[16]分别提出了加入再励学习机制及改进参数设置的改进方式。范小宁等[17]对遗传算法中算子设计及遗传操作进行改进。田鸽等[18]结合2-opt法对蚁群算法的初始信息素、信息素更新方式和启发因子进行改进,从而提高了传统蚁群算法的收敛速度。
在上述水产品的传统配送调度方法探究中,多数学者往往将冰鲜水产品与其他状态的水产品同时作为冷链物流配送考虑,从而忽略了冰鲜水产品的易腐特性对客户满意度的影响。在水产品配送市场激烈竞争下,一个完整的配送调度方案往往要求配送中心同时考虑配送时的路径规划、装箱方案及客户的时间窗需求等多个维度,而考虑单一维度的方案往往只能实现配送过程的路径最短或装箱率最大,无法在控制成本的基础上提高客户满意度。本研究中基于差异化服务的思想,综合考虑客户的现有价值和潜在价值,根据价值理论对客户进行了分类并赋予不同权重,以保证对优质客户满意度的重点关注,同时通过引入前景理论,构造加权平均客户满意度函数,在提高客户满意度的基础上,寻求高效率的冰鲜水产品配送方案。
1 基于前景理论的加权客户满意度函数构建
客户满意度[19]是客户对企业服务质量满意程度的定量表示,体现了客户实际的心理感知效果与其预期期望之间对比的差异情况。随着人们对水产品品质心理预期的提升,水产品企业的服务质量间的竞争也越来越激烈。水产品由于其高度易腐性,在其装载配送过程中又极易受到温度波动、颠簸震荡等因素的影响,因此,当实际送达时间与客户的心理预期时间不符时,客户等待时间越久所需承担的风险越大,客户的心理变化对满意度的影响越显著,因而无法单纯以线性函数来度量此变化过程。传统的期望效用理论过于理想化,将人的主体性忽略不计,而前景理论结合了在客户存在认识偏差时的不确定性,能更为贴近现实地反映客户的满意度。
1.1 基于前景理论的客户满意度函数的构建
考虑到水产品客户在等待冰鲜水产品送达过程中心理及行为因素的影响,本研究中引入前景理论对客户满意度函数进行改进。
1.1.1 前景理论的价值函数 Pan[20]在其综述中指出,前景理论仍然被广泛认为是人们如何在实验环境中评估风险的最佳可用描述,这一理论解释了人们面对风险时的决策表现,即从心理行为学角度出发,决策者设立参考点,通过将决策结果与参考点对比来判断收益或损失。在决策者评估每种选项的价值时,对比后选择最符合心理预期的一种选项并以价值函数的形式表现。价值取决于决策所得结果的变化量,价值曲线V(x)的不对称性表明,一个损失结果减少价值的绝对值大于获利结果增加的绝对值,即人有损失厌恶性。与期望效用理论的不同在于,前景理论中结果的变化量依赖参考点,而不是考虑绝对所得,这也体现了人并非绝对理性。价值函数V(x)的具体表达形式为
(1)
式中:α表示盈利区间的敏感系数;β表示损失区间的敏感系数,敏感系数的取值越小,客观结果的增量在主观价值的反映越弱;λ则反映了损失和收益的相对权重,取值大于1时,损失的权重较高,表示对损失的厌恶。根据Tversky等给出的相关参数值α=β=0.88,λ=2.25。
本研究中在描述客户收到水产品的心理变化时,将心理期望的时间窗端点分别作为获利及面临损失的参考点,当实际送达时间在客户心理预期配送时间内时,则视为收益;而当实际送达时间已经迟于最佳时间,客户的厌恶感知程度不断增加,在超过客户需求时间窗上限时,视为损失。
1.1.2 时间窗设置 本研究中将客户对水产品货物送达的时间窗需求设为[ETi,LTi],其中,i=1,2,…,n为客户节点,ETi为客户i需求的最早送达时间,LTi为客户需求的最晚送达时间。考虑到客户对冰鲜水产品的迫切期望,选定客户需求时间窗的两个端点作为参考点,刘虹等[2]将客户满意度取值设为0.5。当配送车辆能够在客户需求时间窗内送达水产品货物时,越临近最佳服务区间,客户满意度越高。客户心理预期的最优时间窗为![]() 水产品货物在此时间区间内送达时客户满意度达到最高,其中,
水产品货物在此时间区间内送达时客户满意度达到最高,其中,![]() 为客户心理所期望的最早送达时间,
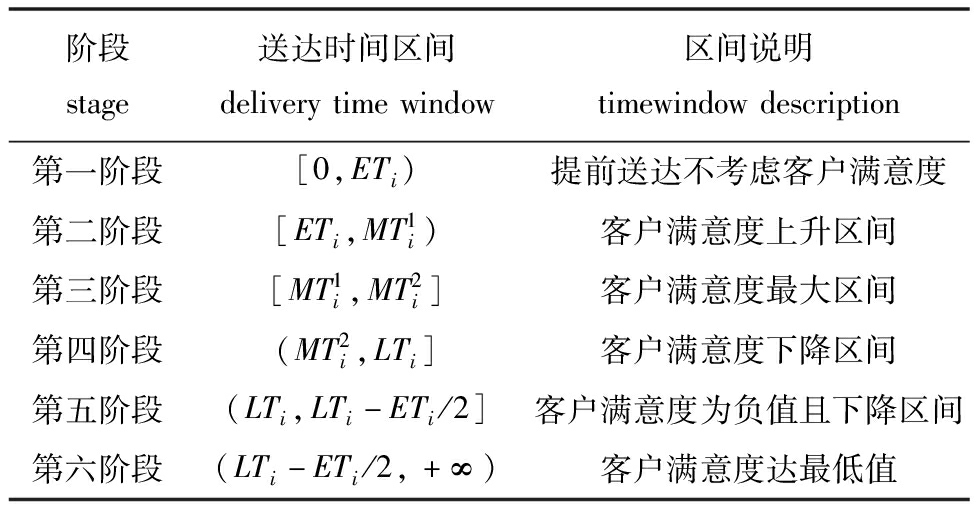
为客户心理所期望的最早送达时间,![]() 为客户心理所期望的最晚送达时间。达到客户最佳服务时间区间时,客户满意度达到最大值为1。当配送车迟于时间窗上限送达水产品货物时,王红等[21]提出水产品在冰鲜条件下的货架期是室温条件下的二倍,结合客户对冰鲜水产品的高时效性要求,本研究假设在半个服务时间窗范围内(时间窗设为(LTi,LTi-ETi/2])客户满意度持续下降,送达时间越晚,则客户心理期望厌恶的程度越高,且满意度表现为负值。当超出(LTi-ETi/2)后客户满意度表现为最低值-1。得出客户满意度与时间区间的关系见表1。
为客户心理所期望的最晚送达时间。达到客户最佳服务时间区间时,客户满意度达到最大值为1。当配送车迟于时间窗上限送达水产品货物时,王红等[21]提出水产品在冰鲜条件下的货架期是室温条件下的二倍,结合客户对冰鲜水产品的高时效性要求,本研究假设在半个服务时间窗范围内(时间窗设为(LTi,LTi-ETi/2])客户满意度持续下降,送达时间越晚,则客户心理期望厌恶的程度越高,且满意度表现为负值。当超出(LTi-ETi/2)后客户满意度表现为最低值-1。得出客户满意度与时间区间的关系见表1。
表1 客户满意度及时间区间关系
Tab.1 Customer satisfaction and time interval relationship
阶段stage送达时间区间deliverytimewindow区间说明timewindowdescription第一阶段[0,ETi)提前送达不考虑客户满意度第二阶段[ETi,MT1i)客户满意度上升区间第三阶段[MT1i,MT2i]客户满意度最大区间第四阶段(MT2i,LTi]客户满意度下降区间第五阶段(LTi,LTi-ETi/2]客户满意度为负值且下降区间第六阶段(LTi-ETi/2,+∞)客户满意度达最低值
1.1.3 客户满意度函数的构建 结合客户收到水产品的现实心理及前景理论的价值函数,第一阶段中,无须考虑客户满意度;第二阶段为客户满意度的上升区间,表现为正收益;第三阶段为最佳服务时间区间,此时客户满意度达到最高;第四阶段为客户满意度的下降区间,但仍在需求时间窗内,表现为正收益;第五阶段已超出客户的需求时间窗,属于延迟配送,客户的不满意程度持续递减,客户表现为不满意,而且随时间推移,客户不满意的程度愈加严重,此时企业为负收益;第六阶段已严重超出客户需求的时间窗,此时的客户满意度达到最低,且不再发生变化。
通过将时间窗端点代入价值函数的方式,得出6个时间区间的客户满意度分段函数为
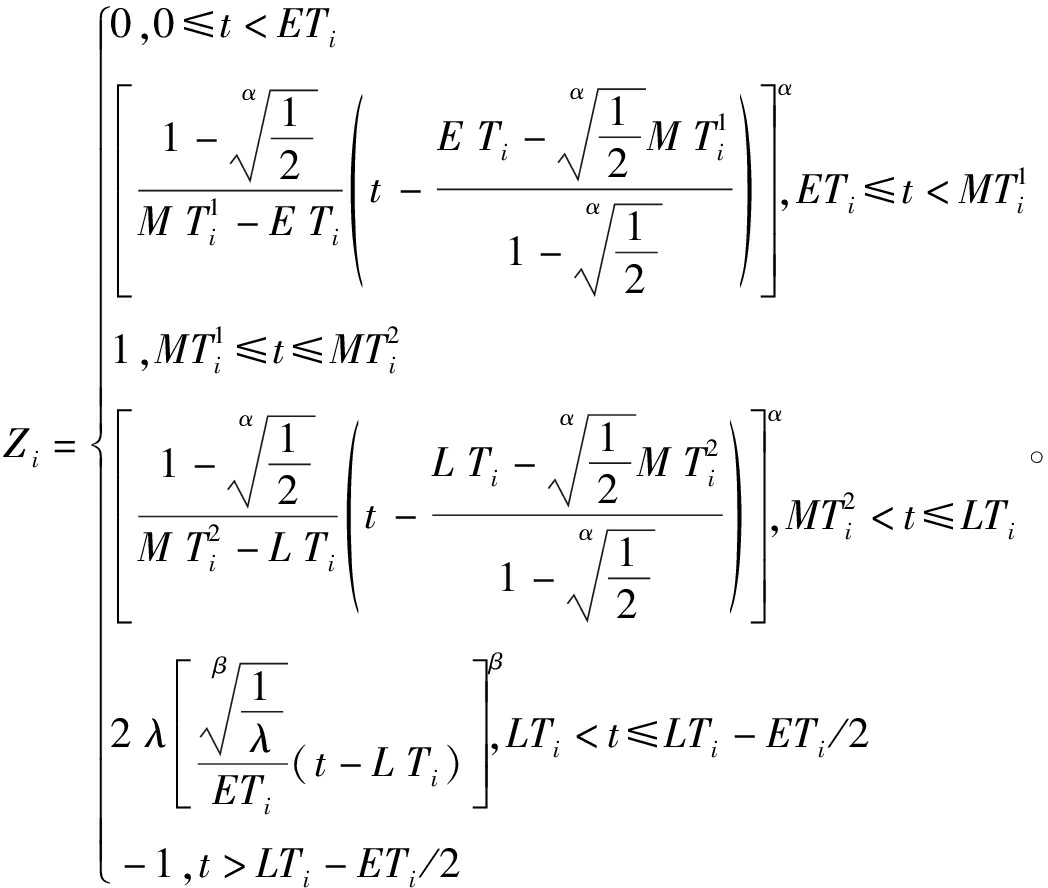
(2)
式中:Zi为客户i的客户满意度;t为实际到达客户i的时刻。
1.2 客户分类
客户分类是指企业依照客户消费行为区分客户群体。帕累托二八定律[22]认为,往往是少数而高质量的投入和努力就能获得大部分有效的产出及报酬。因此,基于全局性考虑可以得出,相比平均对待全部客户,企业对20%的高价值客户投入更多的关注时,反而能获得更多收益。
客户现有价值即客户与企业自交易起给企业带来的全部价值,一般由客户本次购买水产品的价值及历史购买水产品的价值两部分组成。本研究中,假设水产品企业对水产品的定价为a,客户i的需求量为qi,历史价值为HVi,则该客户的当前价值BVi计算公式为
BVi=a×qi+HVi。
(3)
客户潜在价值是指已有客户发掘潜在客户的能力。主要表现为在客户对企业提供的服务满意时,通过对所在社交圈的影响,为企业带来正向反馈并吸引潜在客户。综合现实因素,客户的潜在价值PVi计算公式为
PVi=pcvi×γi×θi×ρi。
(4)
式中:pcvi为潜在客户转化为现有客户时企业能获得的价值,γi为客户的忠诚度,θi为客户i所在社交圈的潜在客户总数,ρi为对潜在客户转化的概率。
综上所述,客户价值可由式(5)表示为
CVi=BVi+PVi。
(5)
在企业制定冰鲜水产品的配送方案时,从企业整体收益角度出发,本研究中应用帕累托二八定律,优先考虑20%客户的满意度。基于客户的现有价值及潜在价值构建客户价值四分矩阵,将客户划分为黄金客户、风险客户、边际客户和普通客户4类。根据帕累托二八定律,由于企业80%的利益来自20%的客户,因此对这部分客户赋予80%的权重。水产品企业在配送冰鲜水产品时,为描述不同类别客户的平均满意程度,将客户的权重Oi作为参数考虑进去,构造加权后的平均客户满意度表达式为
(6)
2 冰鲜水产品多维配送调度模型的构建
2.1 假设条件
在冰鲜水产品的配送过程中,企业需考虑客户的个性化需求。由于冰鲜水产品的易腐性,其质量呈指数变化,因此,必须尽可能在客户的心理预期最佳时间窗内送达,从而保证客户的满意程度。同时,在配送环节中,企业为了保证收益,每辆配送车辆必须规划最短配送路线,并尽量提高装箱率以减少出车数量,从而最大限度地缩减成本。本研究中为突出研究目标,在构建冰鲜水产品的多维配送模型之前,需结合实际应用情况对模型进行合理简化。冰鲜水产品的路径规划及装箱过程相对于传统多回路运输问题,决策变量需针对配送过程中水产品的易腐性做出相应调整。具体如下:
1)配送路径规划的假设条件:①配送车辆完成所有节点的配送任务后返回配送中心;②忽略配送及装卸过程中冰鲜水产品的温度变化;③忽略司机的工时回收需求;④忽略水产品的变质损坏;⑤忽略配送时的规章制度;⑥路径的性质,分为无向和有向,即A点到B点的配送费用不等于B点到A点的配送费用。路径的好坏通过道路的权值来反映;⑦为突出路径规划,假设企业有一个配送中心,与客户节点为一对多关系。
2)三维装箱的假设条件:①冰鲜水产品货箱均为长方体,货箱重心即其几何中心;②货箱不允许倒置或侧置;③冰鲜水产品货箱不允许存在悬空部分,避免在车辆行驶过程中由于路况等因素,造成水产品货箱的晃动或移位;④忽略冰鲜水产品货箱的承重能力;⑤满足装箱的必要约束,包括车厢的载重及容积约束、货箱重量及尺寸约束、货箱装载优先级约束、稳定性约束和重心约束等。
2.2 参数设置
ni表示节点,i=0,1,2,…,n,其中i=0为配送中心,i=1,2,…,n为客户节点。dij表示两客户节点间距离。k表示配送车辆数,k=1,2,…,K,其中K为企业配送车辆总数。li,wi,hi,mi和vi表示客户i需求的水产品货物的长、宽、高、质量及体积。L、W、H、M和V表示配送车辆厢体内部的长、宽、高、最大载质量及最大容积。(XSi、YSi、ZSi)表示客户i的水产品货物的左后下角。(XEi、YEi、ZEi)表示客户i的水产品货物的右前上角。(Xi、Yi、Zi)表示客户i的水产品货物的重心坐标。gi表示客户i需求的水产品货物的重心坐标。[G,G′]表示满足安全几何距离的车厢重心范围。Ski表示配送车辆k遍历客户节点的顺序。Oi表示不同类别的客户i的权重。ai表示客户i所购水产品的价格。valuei表示客户i的价值。hvi表示客户i的历史价值。cvi表示客户i的当前价值。pvi表示客户i的潜在价值。pcvi表示潜在客户转化为现有客户时企业能获得的价值。γi表示客户i对企业的忠诚度。θi表示客户i拥有的潜在客户总数。ρi表示客户i对潜在客户转化的概率。ti表示配送车辆到达客户i节点的时间。Zi表示客户i的客户满意度。
2.3 模型建立
模型以加权平均客户满意度最大为首要目标,在客户满意度最大化的基础上,通过配送路径最短来控制企业成本,并根据现实条件约束建立冰鲜水产品的多维配送调度模型。
目标函数:
(7)
(8)
约束条件:
∑x=ni,
(9)
XEi-XSi=li,YEi-YSi=wi,ZEi-ZSi=hi,
(10)
XEi≤L,YEi≤W,ZEi≤H,
(11)
(12)
Sj≥Si(i,j)∈{(i,j)|Ski>Skj且yki=ykj=1},
(13)
(14)
(15)
ZEi-ZSi=Hi,
(16)
(17)
(18)
(19)
xijk=0或1,i,j=0,1,…,n;∀k,
(20)
ykx=0或1,i=0,1,…,n;∀k,
(21)
ti≥ETi。
(22)
式中:式(7)表示加权平均客户满意度最大;式(8)表示配送路径最短;式(9)表示完全装载;式(10)约束货箱摆放方向为正交或平行;式(11)表示货物均置于配送车的车厢内部;式(12)限制货箱支撑面积均为100%无悬空部分,以保证货车稳定性;式(13)对货箱进行优先级排序,即满足“先下先卸”;式(14)限制装载后车厢的重心位置与其几何中心满足安全几何距离要求;式(15)表示已装载货箱的总质量不得超重;式(16)表示已装载货箱不可倒置;式(17)保证了每个客户的运输任务仅由一辆车完成;式(18)~(21)限制了到达和离开某一客户的冷藏车有且仅有一辆。式(22)表示若配送车辆提前到达客户i需等待。
本研究为防止陷入局部最优解、保持寻觅最优解能力和提高收敛速度,结合2-opt法对蚁群算法的初始信息素、信息素更新方式和启发因子进行了改进。在信息素更新方法中,前10次算法循环中采用本次循环最优解,而在10次后再采用全局最优解更新信息素。这种方法可将解集控制在较优解中,且在收敛速度较快的情况下不会局限解集,保持了继续寻觅最优解的能力。
3 求解算法
3.1 算法简述
目前,求解带有三维装载约束的车辆路径问题(capacitated vehicle routing problem,CVRP)主要存在两种思路:一是分层优化算法,即在规划路径的同时检验三维装箱方案的可行性;二是多阶段优化算法,这种思路将求解过程分为多个阶段,先完成装箱方案,再进行路径的规划,最后将两阶段结合。分层优化算法求解出的方案空间利用率较高,但松弛了“先下先卸”原则,增加了卸载时的成本,故本研究中选用多阶段优化算法,在严格遵循“先下先卸”原则的基础上求解较优方案。即对水产品客户分组赋予不同权重后,先选用模拟退火算法求解三维装箱方案,然后采用改进的蚁群算法调用装箱方案,在保证客户满意度最大的基础上实现对冰鲜水产品多维配送调度模型的高效率求解。
3.2 算法流程主要步骤
1)初始化参数Q、C、α、β、ω,设NC=300(NC为迭代次数),随机将m只蚂蚁放在初始节点。
2)设置循环次数NC=NC+1。
3)设置蚂蚁禁忌表索引号k=1。
4)设置蚂蚁数目变化为k=k+1。
5)通过改进的启发因子函数计算蚁群选择下一段路径的概率,实现其路径移动。
6)判断是否满足约束。
7)调用装箱算法判断装载是否可行:
①输入订单中货箱信息、车厢的容积及载重,以车厢容积为初始空间,基准点为(0,0,0);
②根据优先级对装箱货箱排序,并根据货箱允许的摆放方向生成![]() 个首分支;
个首分支;
③选择分支j,依照从底向上、从左至右、从里往外的顺序进行装箱,即先垂直方向装箱,再水平方向装箱;
④对剩余空间进行切割与合并,然后更新剩余空间及待装货箱;
⑤判断待装货箱是否为空或剩余载重为空,若均不为空则重复迭代步骤⑥和⑦,否则转到步骤⑧;
⑥选择剩余空间,并在剩余待装货箱中,选择重量小于最大剩余载重且优先级最高的货箱进行装载,生成T′个分支;
⑦对T′个分支依照货箱块生成原则构造货箱块,并依照货箱块选择原则进行评估,选择最优构造方案;
⑧令j=j+1,转到步骤3),重复迭代至j=T,结束装箱流程,保留重心最佳方案为最优装箱方案,输出结果。
8)更新蚁群经过路径上的信息素,修改禁忌表。
9)执行步骤2)~7)至每只蚂蚁都选择一条包含全部节点的路径。
10)在所有可行解中寻取最优,即本次迭代最优解。
11)判断循环次数,当NC≤10采用本次循环最优解更新信息素,当NC>10采用全局最优解更新信息素。
12)利用2-opt法进行局部优化。
13)对所有路径更新全局信息素。
14)循环执行步骤2)~12)直到连续多次不出现更优解或达到NCmax,输出为最优解。
4 应用实例
本研究对大连市某水产品配送企业进行调研。选取该企业的25个大连市及周边城市客户订单信息(以序号0表示配送中心,分别以序号1,2,…,25表示配送节点),所使用的配送方案应用传统蚁群算法以最短路径为最优解,以满载率为目标,共由两辆配送车进行配送,总路程346.08 km,配送路线1:0→20→5→24→21→18→25→13→19→10→15→11→16→9→14→6→12→4→23→22→2→1→0;配送路线2:0→17→3→7→8→10→0,并通过调研得到客户满意度为92.30%。
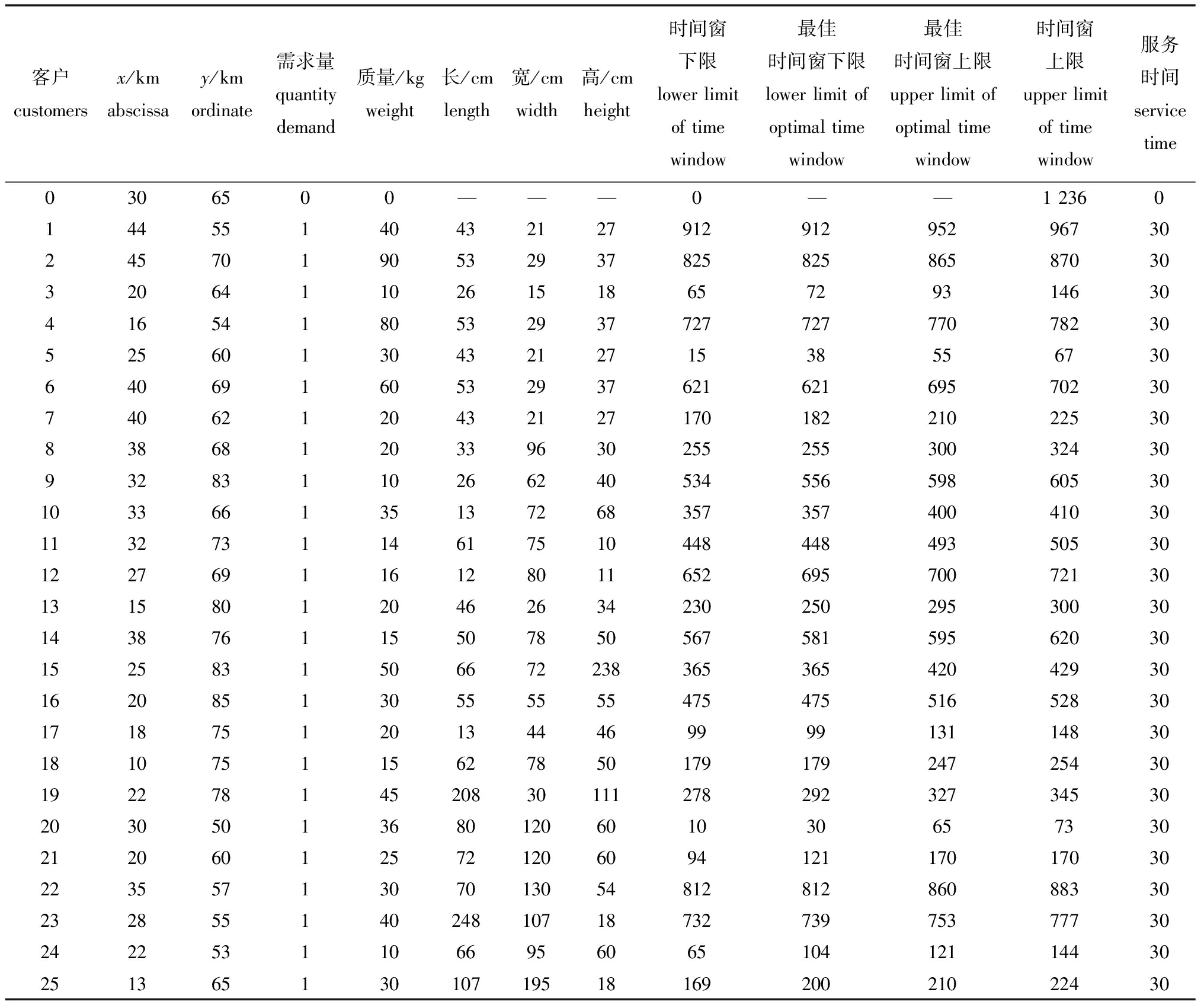
本研究中选取此次25个客户订单的数据作为仿真数据,每个客户订单同时具备客户点地理位置坐标、包装好的水产品货物质量体积及客户需求时间窗等数据信息(表2)。其中,该配送中心的地理位置坐标为(30,65),拥有2辆同样规格负责在省内进行配送的车辆,载重2 300 kg,长305 cm,宽188 cm,高161 cm,行驶速度设为恒定速度60 km/h。每个配送节点(即客户)只能被选择一次,且要求在配送点时间窗需求范围内到达。
表2 客户订单信息
Tab.2 Customer order information
客户customersx/kmabscissay/kmordinate需求量quantitydemand质量/kgweight长/cmlength宽/cmwidth高/cmheight时间窗下限lowerlimitoftimewindow最佳时间窗下限lowerlimitofoptimaltimewindow最佳时间窗上限upperlimitofoptimaltimewindow时间窗上限upperlimitoftimewindow服务时间servicetime0306500———0——12360144551404321279129129529673024570190532937825825865870303206411026151865729314630416541805329377277277707823052560130432127153855673064069160532937621621695702307406212043212717018221022530838681203396302552553003243093283110266240534556598605301033661351372683573574004103011327311461751044844849350530122769116128011652695700721301315801204626342302502953003014387611550785056758159562030152583150667223836536542042930162085130555555475475516528301718751201344469999131148301810751156278501791792472543019227814520830111278292327345302030501368012060103065733021206012572120609412117017030223557130701305481281286088330232855140248107187327397537773024225311066956065104121144302513651301071951816920021022430
4.1 仿真运行
采用SPSS 24及Matlab 2020软件,算例在系统配置为:CPU类型为酷睿双核i处理器、CPU为I-U、内存4 GB、操作系统Windows的环境中对冰鲜水产品配送的装箱方案及路径规划进行仿真。
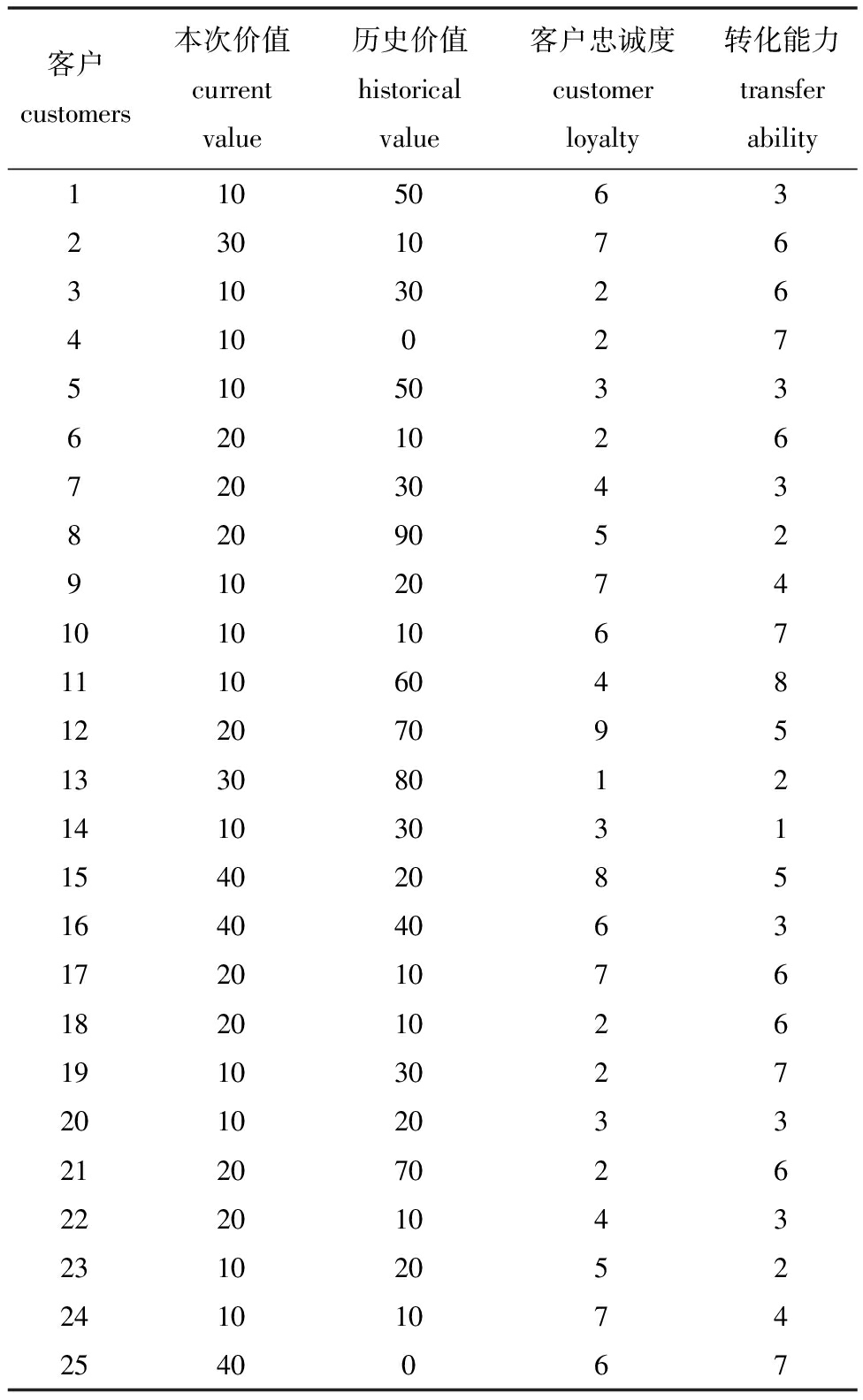
为实现企业客户满意度的最大化,根据“1.2节”提出的帕累托二八定律,对客户群体通过价值进行分类。一个客户的价值往往由该客户的现有价值(本次价值与历史价值)及潜在价值(客户忠诚度及转化能力)衡量,经过调研得到25个客户的价值统计见表3。
表3 客户价值统计
Tab.3 Customer value statistics table
客户customers本次价值currentvalue历史价值historicalvalue客户忠诚度customerloyalty转化能力transferability110506323010763103026410027510503362010267203043820905291020741010106711106048122070951330801214103031154020851640406317201076182010261910302720102033212070262220104323102052241010742540067
应用k-均值聚类法,利用SPSS 24软件将客户分为4类,聚类结果可得:黄金客户有2个,分别是客户8和13;风险客户有4个,分别是客户2、15、16、25。根据帕累托定律,企业应重点关注20%的客户,因此,在25个客户中,前两类共6个客户企业应重点关注,考虑到企业80%的利润来自这两类客户,将其权重分别设为0.4,而由于每类客户的数量不同,分配到每个客户的权重也不同,从而保证了价值越高的客户企业投入越多的关注。边际客户有5个,分别是客户1、5、11、12、21;普通客户有14个,分别是客户3、4、6、7、9、10、14、17、18、19、20、22、23、24,这两类客户不能为企业带来过多利益,因此将其满意度权重分别设为0.1。
对水产品配送中心客户节点的相关数据信息进行300次仿真,取加权后平均客户满意度最大的第192次的迭代解,配送车辆的最优配送方案路线图如图1所示。
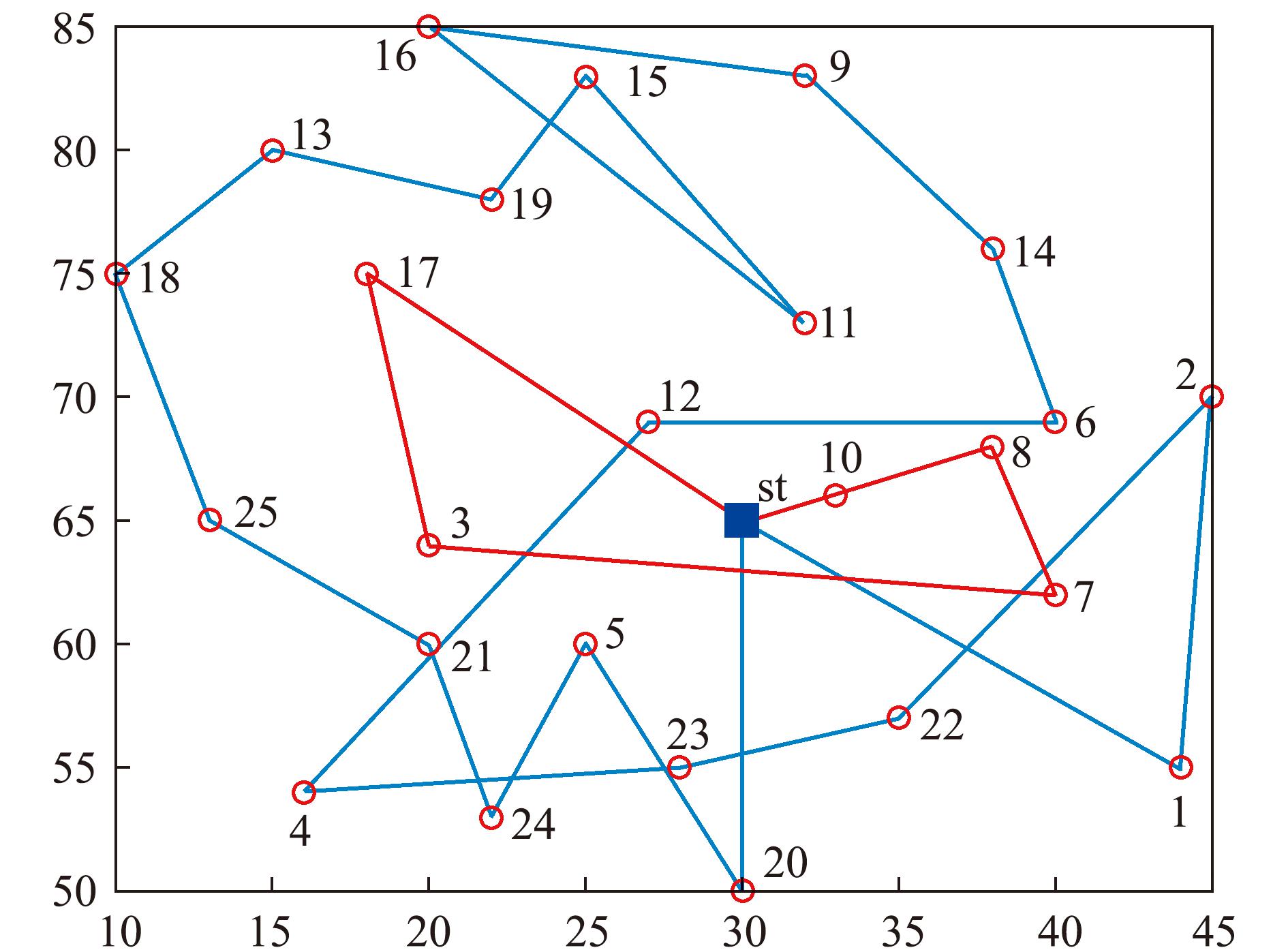
图1 最优配送方案路线
Fig.1 The roadmap for optimal delivery scheme
配送路线3:0→20→5→24→3→21→25→18→13→19→15→11→16→9→14→6→12→4→23→22→2→1→0,配送路线4:0→17→3→7→8→10→0,2辆配送车辆的总配送路径为299.48 km,装箱方案如图2和图3所示,空间利用率分别为88.68%及34.75%,各代平均满意度变化趋势如图4所示。
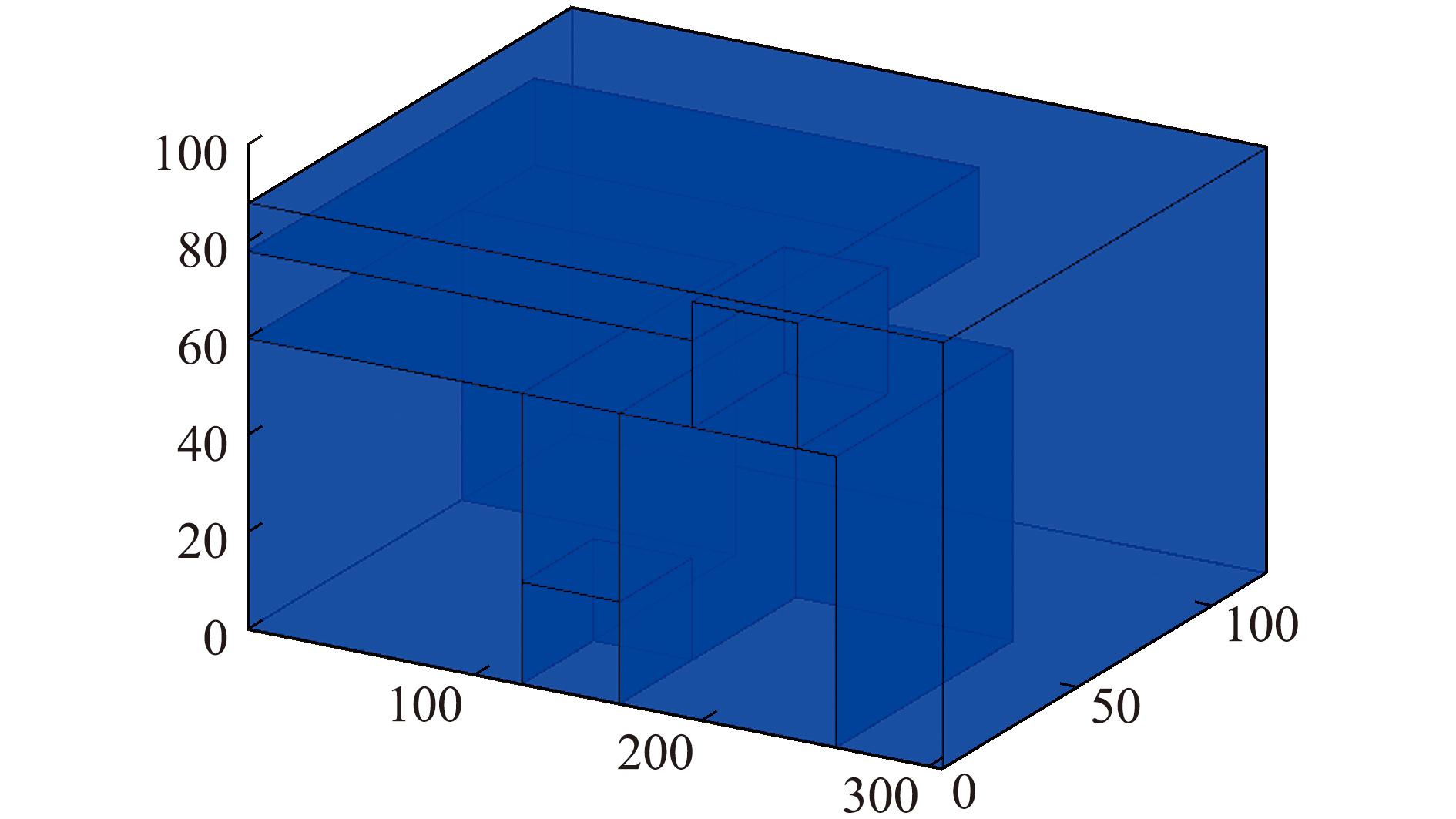
图2 配送路线3装箱方案
Fig.2 The packing scheme for delivery route 3
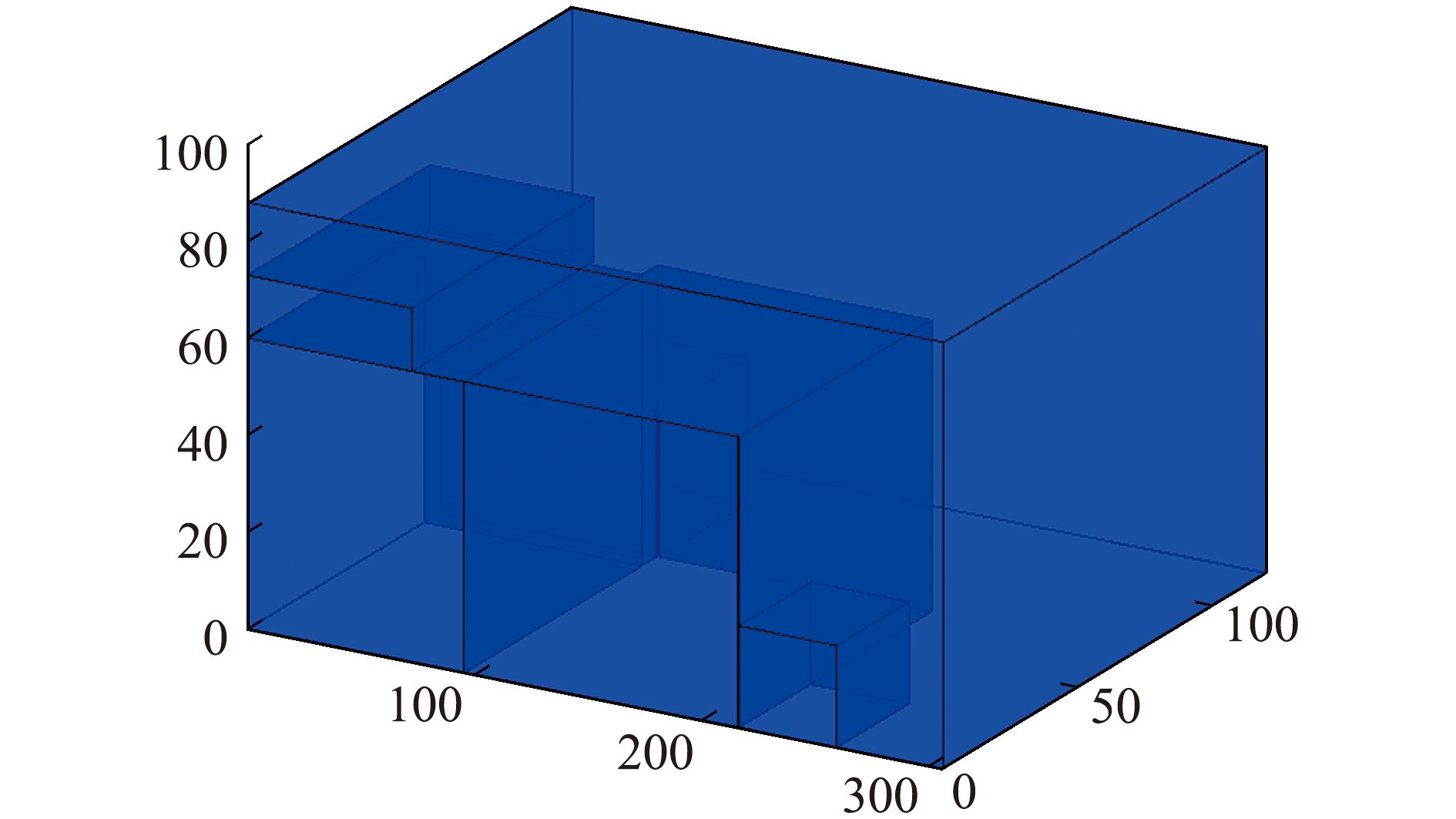
图3 配送路线4装箱方案
Fig.3 The packing scheme for delivery route 4
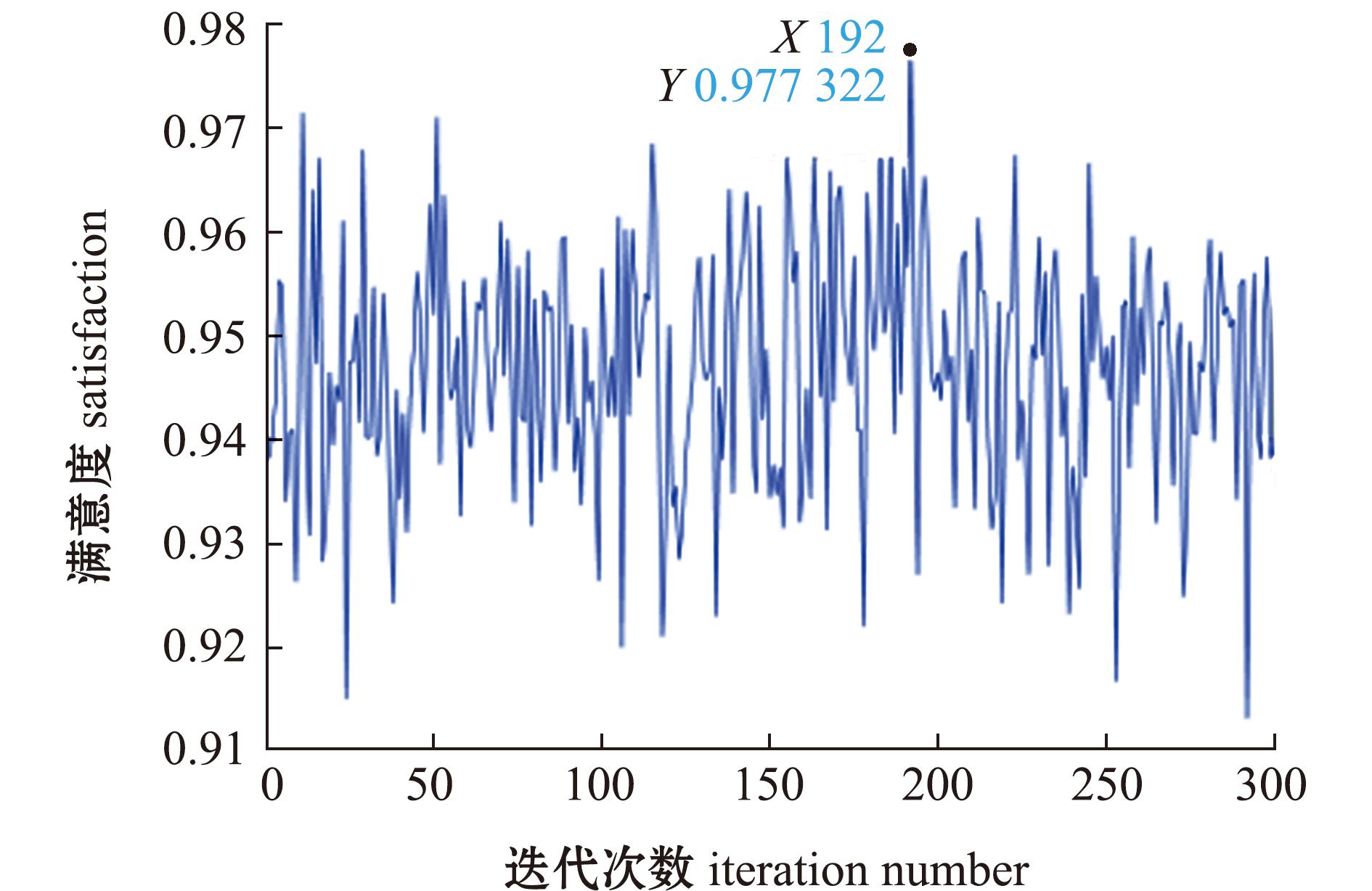
图4 各代满意度平均变化趋势
Fig.4 Trend of averge satisfication for each iteration
冰鲜状态下的水产品在配送时由于以加权后的平均客户满意度最大为首要目标,根据配送中心客户节点的相关信息,选择300次迭代中平均客户满意度最高的第192代解,对配送顺序进行一定调整,得到平均客户满意度为97.73%。
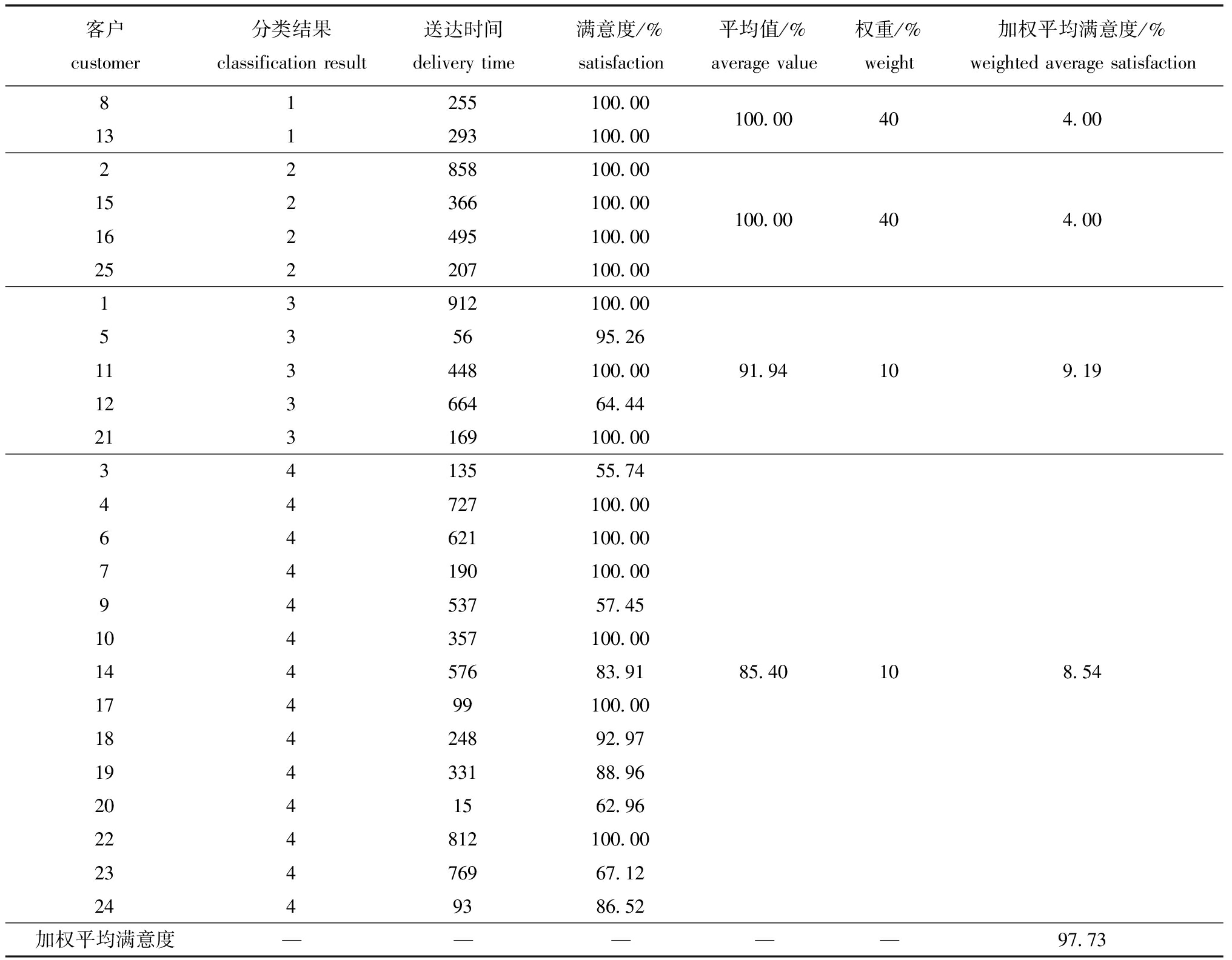
经过Matlab仿真后得到常温和冰鲜水产品25个节点客户的送达时间及满意度见表4,保留小数点后两位。根据前文分析,第一类及第二类客户为优质客户,这两类客户的水产品均在客户要求的最佳时间窗内送达,实现了两类全部客户的满意度达到100.00%。第三类及第四类客户为企业带来的利益不大,但企业保证了在其需求时间窗内送达,第三类客户的平均客户满意度为91.94%;第四类客户的平均客户满意度为85.40%。最终得到加入权重后的总平均客户满意度为97.73%。
表4 水产品送达时间及客户满意度
Tab.4 Aquatic product delivery time and customer satisfaction
客户customer分类结果classificationresult送达时间deliverytime满意度/%satisfaction平均值/%averagevalue权重/%weight加权平均满意度/%weightedaveragesatisfaction81255100.00100.00404.00131293100.0022858100.00152366100.00100.00404.00162495100.00252207100.0013912100.00535695.26113448100.0091.94109.1912366464.44213169100.003413555.7444727100.0064621100.0074190100.009453757.45104357100.0014457683.9185.40108.5417499100.0018424892.9719433188.962041562.96224812100.0023476967.122449386.52加权平均满意度—————97.73
通过运用SPSS24对客户进行k-均值聚类,对不同重要程度的客户赋予权重。并针对启发式算法的参数进行仿真实验,确定关键参数的具体数值,得到常温与冰鲜状态下的水产品即时配送多维调度方案。从优化前后对比分析可知(表5),相比企业原始的配送调度方案,本研究中的冰鲜水产品配送调度方案以平均客户满意度最大为主要目标,得到两条配送路径,总路径为299.48 km,实现了97.73%的加权平均客户满意度,总路程相对当前企业的调度方案缩短了15.56%,客户满意度提高了5.88%,有效提升了冷链配送企业的市场竞争力。
表5 优化前后结果对比
Tab.5 Comparison of results before and after optimization

配送方案deliveryschemes总路程/kmtotaldistance客户满意度/%customersatisfaction与企业原始配送调度方案对比originaldistributionschedulingplan路程缩短程度/%distancereductionratio满意度提高程度/%satisfactionenhancementratio企业配送调度方案346.0892.30——冰鲜状态配送方案299.4897.7315.565.88
5 结论
本研究中针对高度易腐的冰鲜水产品的客户满意度问题,根据客户价值理论将客户群体分类赋予权重,通过引入前景理论构建6个配送时间区间的客户满意度函数,加入权重推导得到度量平均客户满意度的表达式。最终得到冰鲜水产品的总配送路径距离相比企业原方案缩短了15.56%,平均客户满意度达到97.73%,相比企业原始配送方案提高了5.88%。本研究结果为加速冷链物流的发展拓宽了解决思路,也为冰鲜水产品的即时配送调度提供了理论支持。
[1] 黄益平,杨琴,李青,等.考虑客户等待时间感知的快递车辆优化调度[J].工业工程,2017,20(4):31-36,48.HUANG Y P,YANG Q,LI Q,et al.The delivery vehicle scheduling considering agents’ perception satisfaction toward waiting time[J].Industrial Engineering Journal,2017,20(4):31-36,48.(in Chinese)
[2] 刘虹,林楚玥.考虑时间窗服务价值的越库车辆路径优化[J].西安电子科技大学学报(社会科学版),2019,29(2):12-23.LIU H,LIN C Y.Optimization for vehicle routing problem with cross-docking considering the value of time window service[J].Journal of Xidian University (Social Science Edition),2019,29(2):12-23.(in Chinese)
[3] GANJI M,KAZEMIPOOR H,HADJI MOLANA S M,et al.A green multi-objective integrated scheduling of production and distribution with heterogeneous fleet vehicle routing and time windows[J].Journal of Cleaner Production,2020,259:120824.
[4] 于江霞,杜红亚,罗太波.基于客户分类的即时配送路径优化研究[J].交通运输系统工程与信息,2020,20(4):202-208.YU J X,DU H Y,LUO T B.Real-time delivery routing optimization based on customer classification[J].Journal of Transportation Systems Engineering and Information Technology,2020,20(4):202-208.(in Chinese)
[5] YAMADA S,ISHIGAKI A,YAMADA T.Customer satisfaction and timely delivery:the order picking scheduling problem[J].Innovation and Supply Chain Management,2018,12(2):21.
[6] WANG X P,SUN X Y,DONG J,et al.Optimizing terminal delivery of perishable products considering customer satisfaction[J].Mathematical Problems in Engineering,2017,2017(1):8696910.
[7] 王勇,张杰,刘永,等.基于时间窗和温度控制的生鲜商品物流配送优化方法[J].控制与决策,2020,35(7):1606-1614.WANG Y,ZHANG J,LIU Y,et al.Optimization method study of fresh good logistics distribution based on time window and temperature control[J].Control and Decision,2020,35(7):1606-1614.(in Chinese)
[8] 李畅,陈淮莉.基于新鲜度和配送成本的易腐食品配送路径[J].上海海事大学学报,2019,40(1):14-20,36.LI C,CHEN H L.Distribution route of perishable food based on freshness and distribution cost[J].Journal of Shanghai Maritime University,2019,40(1):14-20,36.(in Chinese)
[9] KURPEL D V,SCARPIN C T,P CORA J E Jr,et al.The exact solutions of several types of container loading problems[J].European Journal of Operational Research,2020,284(1):87-107.
CORA J E Jr,et al.The exact solutions of several types of container loading problems[J].European Journal of Operational Research,2020,284(1):87-107.
[10] MAHVASH B,AWASTHI A,CHAUHAN S.A column generation-based heuristic for the three-dimensional Bin packing problem with rotation[J].Journal of the Operational Research Society,2018,69(1):78-90.
[11] DORNAS A H,MARTINS F V C,SARUBBI J F M,et al.Real-polarized genetic algorithm for the three-dimensional Bin packing problem[C]//Proceedings of the Genetic and Evolutionary Computation Conference.Berlin Germany.ACM,2017:785-792.
[12] 雷定猷,宋文杰,张英贵.平衡装载约束下的车辆路径问题研究[J].计算机应用研究,2020,37(6):1622-1625,1641.LEI D Y,SONG W J,ZHANG Y G.Research on vehicle routing problem under balance loading constrain[J].Application Research of Computers,2020,37(6):1622-1625,1641.(in Chinese)
[13] 高梦伟,卢玮.智能配送车拼箱装车和路径优化问题研究[J].物流科技,2018,41(8):104-108.GAO M W,LU W.Research on the LCL loading and vehicle routing problem of smart distribution vehicle[J].Logistics Sci-Tech,2018,41(8):104-108.(in Chinese)
[14] CASTELLUCCI P B,TOLEDO F M B,COSTA A M.Output maximization container loading problem with time availability constraints[J].Operations Research Perspectives,2019,6:100126.
[15] 董凌艳,徐红丽.基于改进型蚁群算法的AUV路线规划[J].自动化与仪表,2017,32(3):1-4.DONG L Y,XU H L.Route planning of AUV based on improved ant colony algorithm[J].Automation and instrumentation2017,32(3):1-4.(in Chinese)
[16] 周卫标,吴楚东,高敏.基于改进蚁群算法的配送路线优化分析[J].科技经济导刊,2018,26(15):10-11.ZHOU W B,WU C D,GAO M.Optimization analysis of distribution route based on improved ant colony algorithm[J].Technology and economy Guide,2018,26(15):10-11.(in Chinese)
[17] 范小宁,徐格宁,杨瑞刚.车辆配送路径优化的新型蚁群算法[J].计算机工程与应用,2011,47(26):232-234,245.FAN X N,XU G N,YANG R G.New ACO algorithm for optimizing of vehicle distribution routing[J].Computer Engineering and Applications,2011,47(26):232-234,245.(in Chinese)
[18] 田鸽,薛冬娟,梁斌,等.基于改进蚁群算法的冰鲜水产品配送路径优化方法研究[J].大连海洋大学学报,2019,34(5):746-751.TIAN G,XUE D J,LIANG B,et al.Distribution route and its optimization of chilled fishery products[J].Journal of Dalian Ocean University,2019,34(5):746-751.(in Chinese)
[19] ZHENG C J,SUN K,GU Y H,et al.Multimodal transport path selection of cold chain logistics based on improved particle swarm optimization algorithm[J].Journal of Advanced Transportation,2022,2022:5458760.
[20] PAN Z.A review of prospect theory[J].Journal of Human Resource and Sustainability Studies,2019,7(1):98-107.
[21] 王红,王少华,熊光权,等.水产品保鲜技术研究及发展趋势[J].湖北农业科学,2019,58(12):15-18.WANG H,WANG S H,XIONG G Q,et al.Research progress and development trends of aquatic products preservation technology[J].Hubei Agricultural Sciences,2019,58(12):15-18.(in Chinese)
[22] DUNFORD R,SU Q,TAMANG E,et al.The pareto principle[J].The Plymouth Student Scientist,2014,7(2):140-148.