太湖位于长江三角洲南缘,是中国五大淡水湖之一。太湖水产养殖业主要依赖于定居性鱼类、江海洄游性鱼类和江湖半洄游性鱼类,其中“太湖三白”(银鱼、白虾和白鱼)是其最重要的经济鱼类,年渔业产量约为7.2万t,渔业产值达6.5亿元[1]。然而,经济发展伴随的水质富营养化和蓝藻水华问题日益凸显,严重威胁太湖的生态平衡并对水产养殖业构成隐患。水质作为水生动物生存的基石,其优劣直接关系到水生动物的生长状况与健康水平。其中,pH值是维持水体稳定的关键,其变化影响水生生物的生理活动、代谢过程,从而影响生态系统健康与动植物的正常生长[2]。
在新一代信息技术的驱动下,人工智能、大数据及机器学习等先进技术的快速发展,为精确预测养殖水环境提供了强大的技术支撑。借助这些现代科技手段,国内外研究者已着手开展了一系列深入的养殖水体水质预测研究工作。
在水质预测的实践中,统计学模型被广泛采用。籍淑芳等[3]利用模糊聚类和统计学方法研究了北京昌平区的地下水质状况。李婉君等[4]运用聚类分析对珠江三角洲地区的水质进行了分类研究。万蕾等[5]通过相关分析发现,云龙湖中总磷含量与化学需氧量(COD)紧密相关,而总氮与氨氮的关联则相对较弱。张稳[6]则应用描述性统计学对季节性水质数据进行分析,并通过非参数检验技术探讨了不同季节间水质浓度的变化。Galoie等[7]通过非线性多元回归分析成功预测了沙尘暴期间水质指数,助力改善了水质决策。尽管这些方法为水质分析提供了有力的工具,但由于水产养殖环境的多变性,以及pH值与其他水质指标的复杂关联性,这些传统方法在处理多维和非线性的水产养殖水质预测时,仍需进一步提升性能。
在水质管理的前沿,深度学习技术也正逐渐崭露头角,尤其在预测水质参数这一领域[8]。相较于传统的统计学手段,深度学习在处理复杂函数拟合、数据挖掘和特征抽象化等任务上有着明显的优势[9-10]。李彦杰等[11]的研究证实LSTM在多项评价指标上超越了SVR模型。顾乾晖等[12]通过引入QPSO算法优化的LSTM网络,同样在准确性上取得了显著进步。Gao等[13]则通过LSTM模型预测关键水质参数,提高了水资源管理的准确性。然而,尽管深度学习技术在水质管理领域取得了显著成就,但传统方法和单一的深度学习模型仍存在准确性和鲁棒性不足的问题,为应对这些挑战,研究者需开发出更为先进的组合模型。
在组合模型方面,Zhang等[14]开发的EMD-LSTM模型,通过结合数据预处理和深度学习,显著提升了无试剂水质检测的准确性和可持续性。Rasheed等[15]验证了结合CNN和LSTM的模型在运算效率和处理复杂度上的双重优势。Zhang等[16]所开发的混合CNN-LSTM模型在预测地源热泵系统方面尤其出色。另外,石庆兰等[17]采用BiLSTM和GRU的混合模型在多个性能指标上优于传统LSTM模型。Chen等[18]提出的AEABC-BPNN模型显著提高了河流水质指数预测的准确性和鲁棒性。Tian等[19]提出的DeepTCN-GRU模型通过结合CNN和RNN技术,显著优化了黄河水源区水质的pH和TN的预测性能。而Guo等[20]则成功构建了融入气候变量的多维LSTM网络,有效提升了黄河流域NDVI的预测精度。张雪薇等[21]通过结合循环神经网络(RNN)和卷积神经网络(CNN)的ConvGRU深度学习模型,有效预测了2020年西北太平洋部分海域的海表面温度。
尽管上述研究在预测单个水质参数方面取得了一定成果,但忽略了被预测水质指标与其他水质指标间的相关性。针对上述问题,本研究中提出了一种融合LSTM神经网络和XGBoost模型的水质pH值预测方法(PCA-ES-LSTM-BSO-XGBoost,PELBX),提高了pH预测的精度,并通过试验验证了其准确性与有效性,以期为水产养殖生态系统平衡及水生动物的健康提供有益参考。
1 研究方法
本研究中提出的PELBX水质pH预测模型:首先,运用PCA降维技术对原始水质数据进行处理,旨在简化数据结构并保留关键信息;其次,利用LSTM网络捕获水质参数随时间变化的动态特性,通过早停法增强其长期依赖关系的捕捉能力,有效避免过拟合,同时,采用贝叶斯优化算法(behavioral swarm optimization,BSO)的XGBoost模型来预测pH变化率,使其能够探索更大的参数空间,进而获得更高精度的解;最后,将LSTM和XGBoost模型的结果进行加权集成,并结合时间序列分析与非线性学习的优点,实现对pH指标变化率的精准预测,模型架构如图1所示。

图1 预测模型流程
Fig.1 Flowchart of the prediction model
1.1 数据预处理
1.1.1 异常值处理 在水质监测数据中,pH值应维持在一定的生态平衡范围内,若突然出现极端的pH读数(可能由仪器故障、操作失误或特定污染事件引起),且这些数据点未被正确识别并处理,可能会导致模型错误地将这些异常读数解释为正常波动。这种误解可能使模型在遇到正常的pH变化时反应过度或不足,影响其对其他正常数据的预测能力。更严重的是,模型可能会在未来预测中将这些异常值视为常态,从而减少其对真实水质变化的敏感性和响应性(未经预处理的pH数据对预测模型精度影响详见“2.2.1节”的试验部分)。
基于上述需求,采用Z分数方法处理整个数据集中的异常值,通过计算分数并移除极端值,确保模型在训练和预测时的数据质量,提高对太湖水质变化的敏感性和预测准确性。基于经验规则[22],若某个数据点的Z分数绝对值超过3,则被视为异常值,并可从数据集中移除以避免对预测结果造成偏差。在移除异常值后,为平滑日常环境波动对数据的影响,模型采用高斯滤波器对数据进行平滑处理,为后续的模型建立提供稳定的数据基础。
1.1.2 相关性分析 本研究中对太湖水质数据进行了深入分析,该数据集涵盖了16种不同的水质指标。为了探究pH值与其他水质指标间的潜在关联,同时在输入预测模型时能够提高pH值预测的精度,采用皮尔逊相关系数对pH值与其他水质指标进行相关性分析。从图2可见,pH值与透明度、硝酸盐氮和氨态氮等呈现出显著的负相关性,其相关系数分别为-0.22、-0.30和-0.28;同时,pH值与水温、硅酸盐、化学需氧量和总磷间呈现出正向的强相关,相关系数分别为0.33、0.20、0.29和0.27。此外,溶解氧、亚硝酸盐氮和总氮与pH值之间存在中等程度的负相关,相关系数分别为-0.09、-0.12和-0.12,意味着这些成分含量的增减也会与pH值的变化相关联。由此可以得出pH值与水温、溶解氧、亚硝酸盐氮、硝酸盐氮、氨态氮和总氮等15种指标存在相关性,能够共同作为预测模型训练的参数。
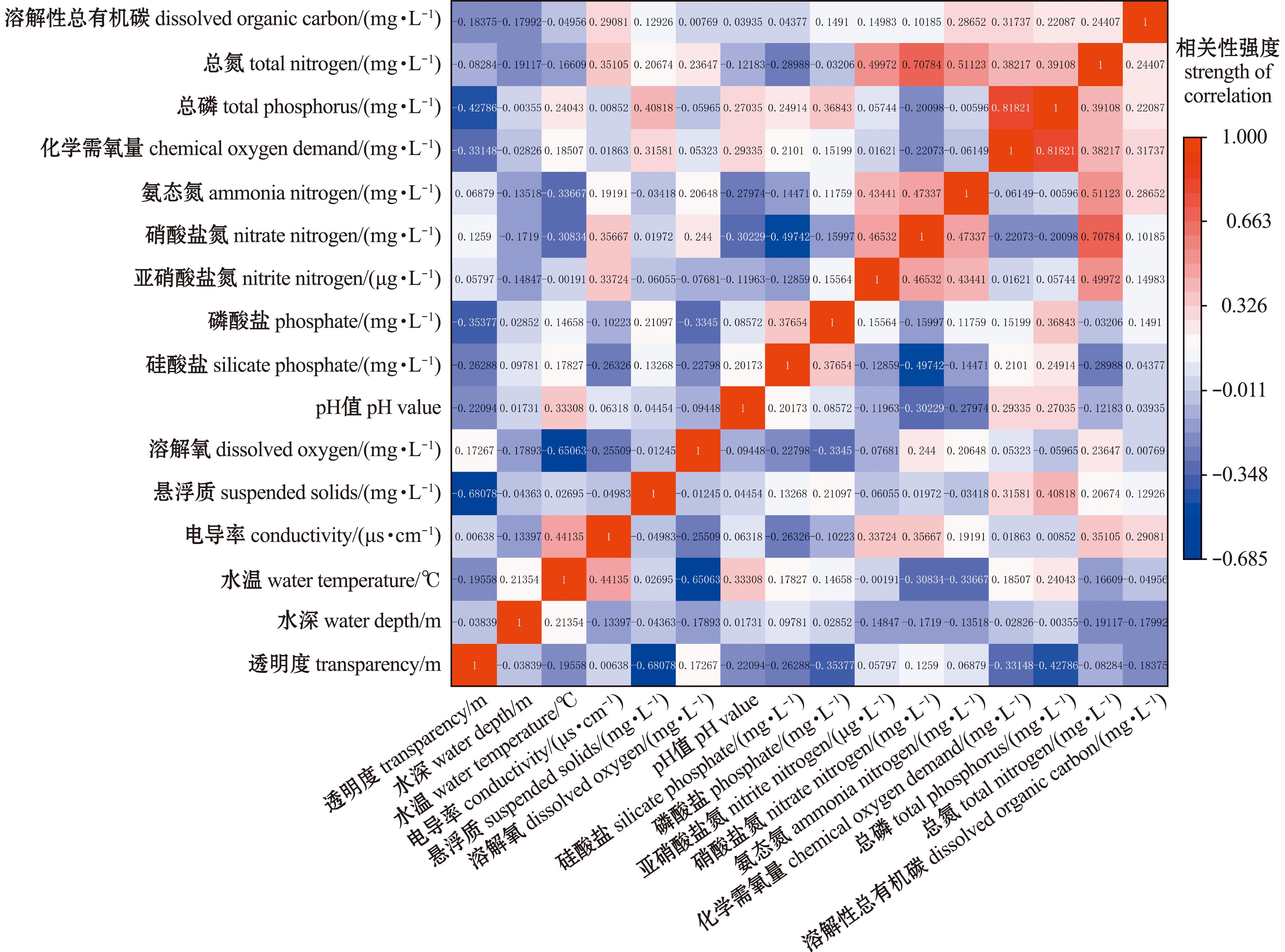
图2 太湖水质各指标与pH值的相关性热力图
Fig.2 Heatmap of the correlation between various water quality indicators and pH value in Taihu Lake
1.1.3 数据标准化与PCA降维 由于溶解氧、水温、亚硝酸盐氮和硝酸盐氮等参数具有不同的量纲和测量单位,直接将这些不同量纲的数据输入到模型中可能会导致一些参数由于量纲大而对模型产生不成比例的问题。所以对选取后的太湖水质数据采用标准化和归一化处理,确保所有参数在同一尺度下进行比较,以消除量纲的影响。
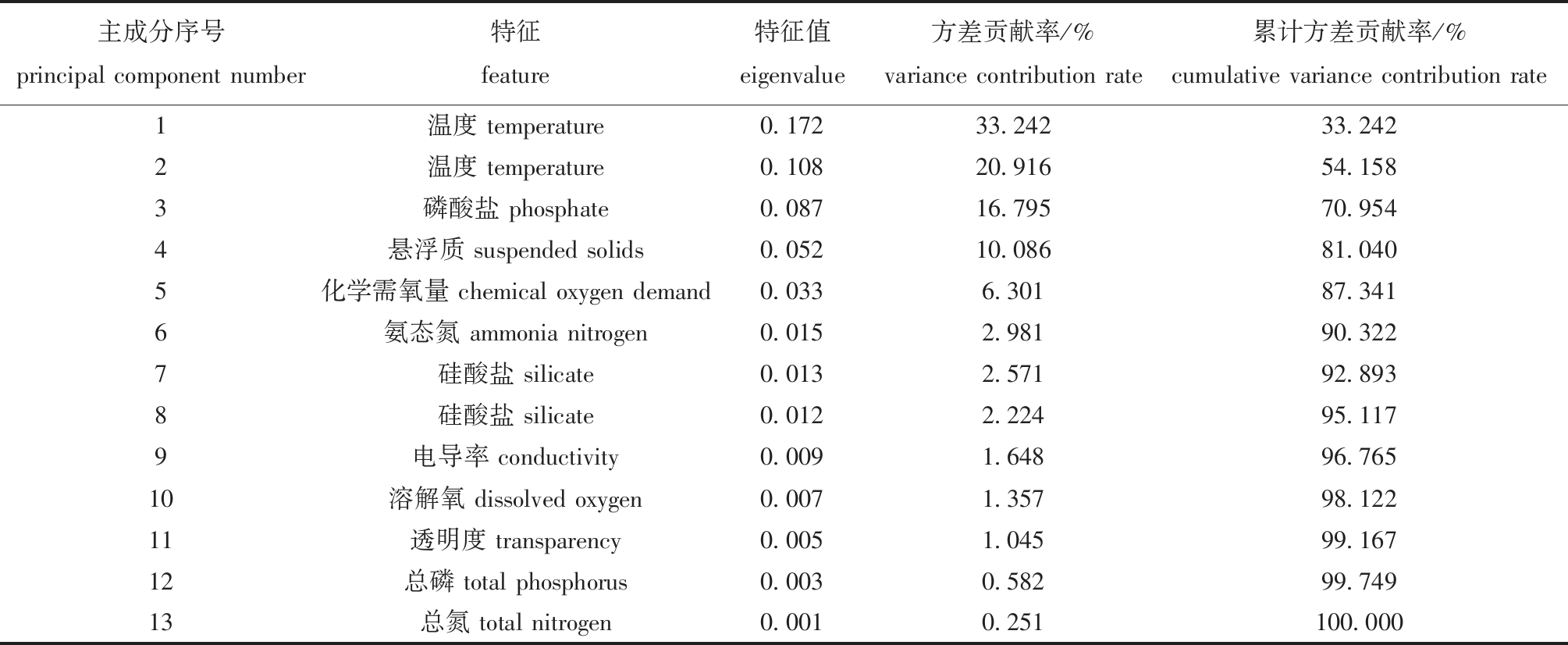
数据标准化和归一化处理后,使用主成分分析(principal component analysis,PCA)方法对数据进行降维。降低模型计算的复杂度,帮助模型更有效地捕捉关键特征,从而进一步提高对pH值变化的预测精度。从表1可见,当将太湖养殖水质数据降至13维时,累计方差贡献率达到了100%,这意味着原始数据的信息被最大程度保留。因此,在预测pH值的过程中,选择13维作为该模型的输入,以提升模型的运算效率。
表1 PCA降维后的方差贡献率
Tab.1 Variance contribution rate after PCA dimensionality reduction
主成分序号principal component number特征feature特征值eigenvalue方差贡献率/%variance contribution rate 累计方差贡献率/%cumulative variance contribution rate 1温度 temperature0.17233.24233.2422温度 temperature0.10820.91654.1583磷酸盐 phosphate0.08716.79570.9544悬浮质 suspended solids0.05210.08681.0405化学需氧量 chemical oxygen demand0.0336.30187.3416氨态氮 ammonia nitrogen0.0152.98190.3227硅酸盐 silicate0.0132.57192.8938硅酸盐 silicate0.0122.22495.1179电导率 conductivity0.0091.64896.76510溶解氧 dissolved oxygen0.0071.35798.12211透明度 transparency0.0051.04599.16712总磷 total phosphorus0.0030.58299.74913总氮 total nitrogen0.0010.251100.000
1.2 预测模型构建
1.2.1 基于LSTM模型的pH指标预测方法构建与优化 由于太湖水质参数中pH值与溶解氧、水温等参数之间的相关性,本研究中选择将LSTM层的隐藏单元设置为50,此设置有助于捕捉更多的指标之间时间动态信息。同时,学习率被设定为0.001,较低的学习率意味着模型参数更新的步伐较小,能够使模型更细致地适应水质数据的总体趋势,而不是对特定噪声或异常数据做过度反应,也有利于保持训练过程的稳定性,避免因学习率过高而导致的参数更新过大,进而引发模型训练过程中的震荡或不稳定现象。
基于LSTM预测pH值网络模型主要包含4个核心部分:1)遗忘门负责决定哪些历史水质信息应被丢弃,以避免无关信息干扰未来pH值变化的预测;2)输入门则决定哪些新的水质信息应被更新到细胞状态中,这对于捕捉当前环境下水质变化至关重要;3)细胞状态本身作为网络的记忆单元,持续追踪水质参数随时间的变化,其细胞状态的更新通过合并遗忘门的结果和输入门的结果来完成;4)最后,输出门控制从细胞状态中提取关键信息形成对未来pH变化的预测输出。
LSTM预测模型中,权重矩阵和偏置项通过对太湖水质历史数据的学习来获得,这些参数能够处理输入的水质数据和历史信息,并通过Sigmoid和双曲正切(tanh)激活函数来模拟水质变化背后的复杂非线性关系。
为确保模型在学习太湖水质数据时能够泛化到未见过的数据,而不仅仅是记忆训练集,采用了早停策略(early stopping),防止过拟合现象出现,以排除无关的随机噪声。此外,为了优化模型,选择了Adam优化器进行参数的调整,通过自动调整学习率来适应每个参数的特定变化,从而帮助模型更快收敛,保持对过往水质动态的敏感性的同时,发掘出更多有价值的预测信息。
1.2.2 基于XGBoost模型的pH指标预测方法构建与参数优化 本研究中,针对太湖水质pH值预测的需求,采用极端梯度提升(extreme gradient boosting,XGBoost)模型,并通过贝叶斯优化算法(BSO)对其超参数进行了精细调整。由于XGBoost模型的性能高度依赖于超参数配置,如树的最大深度、学习率、树的数量和子样本比例等,因此本研究中利用贝叶斯算法模拟自然生物群体行为模式,在探索更大参数空间的同时避免了局部最优解,从而全面提升了模型对pH值的预测精度。该优化过程基于交叉验证下的均方根误差(RMSE)评估,旨在最小化误差并确保模型在预测太湖水质参数时达到最佳性能。通过这种方法,本研究中期望在保留太湖水质数据特征的同时,减少模型对噪声数据的敏感度,提高预测准确性。
1.2.3 集成模型 集成模型结合了LSTM和XGBoost模型的预测能力,通过对两者预测结果的加权平均,以期获得更准确的综合预测。
(1)
式中:pred为集成预测结果;lstm_pred为LSTM模型的预测结果;而xgb_pred为经过贝叶斯优化的XGBoost模型的预测结果。
2 试验与分析
2.1 数据集介绍及模型评价指标
2.1.1 数据集介绍 本研究中采用太湖2007—2015年中8个水质监测站观测的水质数据,共计865条数据。对本文提出PELBX的pH预测方法正确性和性能进行验证,数据集被划分为训练集和测试集,比例为4∶1。
2.1.2 模型评价指标 为了评估PELBX预测方法对pH参数的预测性能,本文采用了4个评价指标:均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)及决定系数(coefficient of determination,R2),其中,RMSE、MAE和MAPE的值越小,代表预测值越能接近真实值,表示模型的预测性能越好;R2的值越接近1,表示模型的预测效果越好,能够更准确地反映观测值的变化。
2.2 试验
2.2.1 未经预处理数据对模型影响的对比试验 数据预处理不仅能提升学习效率、缩减训练时长,还能增强模型预测的可信度和用户接受度。为了评估数据预处理对模型准确性和可靠性的提升效果,本研究中通过对比使用未预处理和已预处理数据进行预测的结果来进行分析。
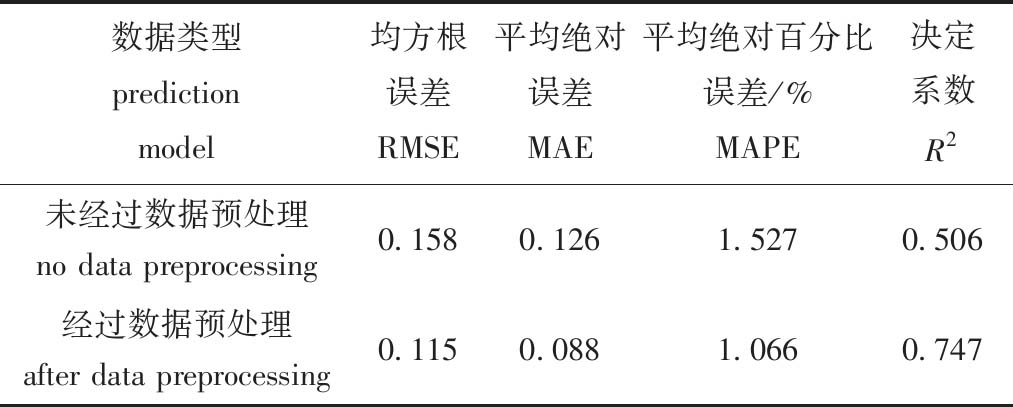
从图3可以明显观察到数据预处理在PELBX网络模型中对水质pH值预测性能的显著影响。使用预处理后的数据进行预测,其预测值曲线与实际数据曲线更为吻合,且波动性显著降低。在极端值和波动点上,预处理数据的预测表现远胜于未预处理数据。这表明数据预处理对于减小预测结果的偏差和提升稳定性具有重要作用,从而使预测更为精确和平滑。从表2可见,数据预处理后相较于之前均方根误差、平均绝对误差和平均绝对百分比误差分别降低了27.22%、30.16%和30.19%,决定系数提高了47.63%,证明了数据预处理在优化模型预测性能方面的有效性。
表2 数据预处理前后评价指标对比结果
Tab.2 Comparison results of evaluation indicators before and after data preprocessing
数据类型prediction model均方根误差RMSE平均绝对误差 MAE平均绝对百分比误差/%MAPE决定系数R2未经过数据预处理no data preprocessing0.1580.1261.5270.506经过数据预处理after data preprocessing0.1150.0881.0660.747
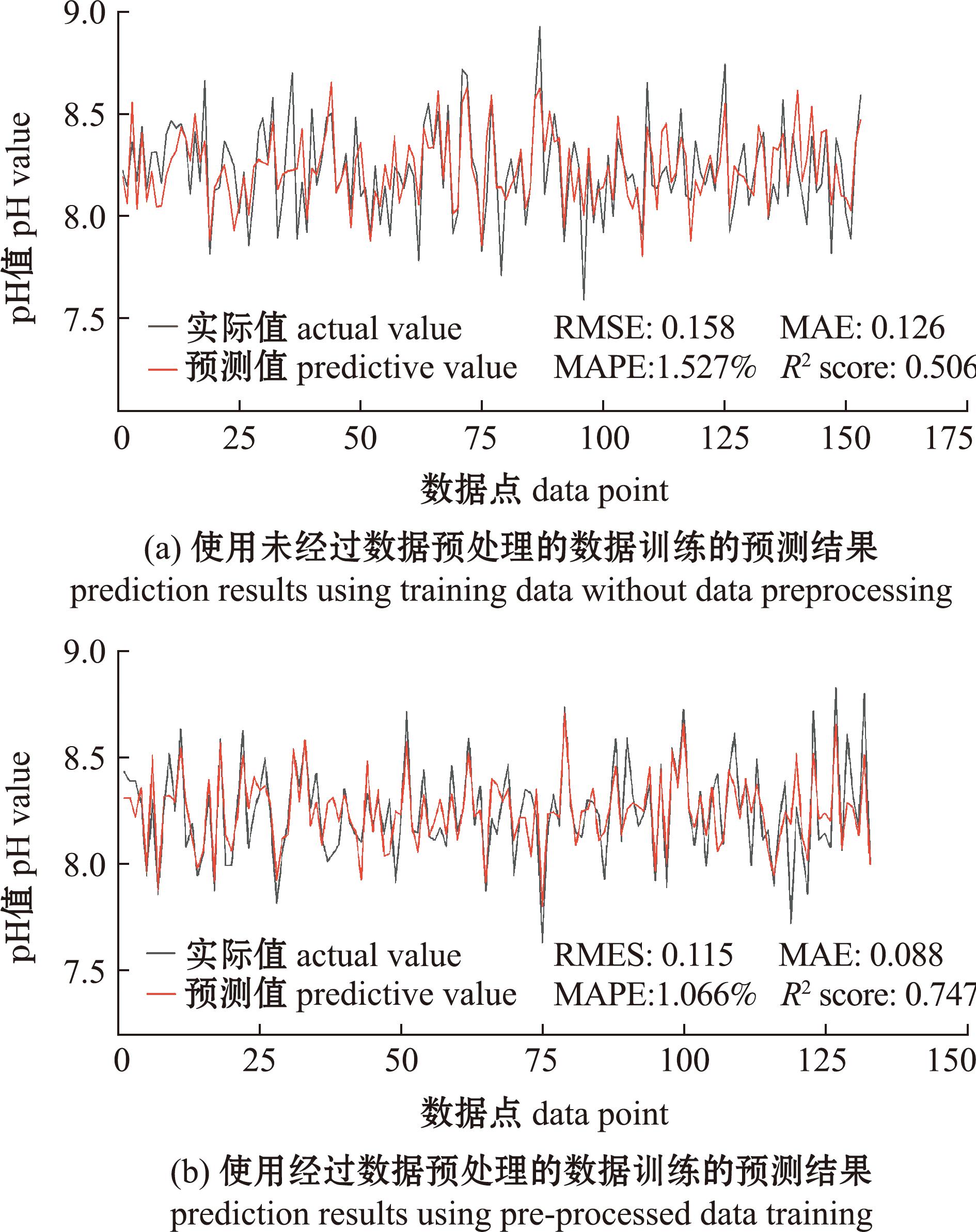
图3 数据预处理前后预测结果对比
Fig.3 Comparison of prediction results before and after data preprocessing
2.2.2 损失函数对比试验 损失函数作为衡量模
型性能的关键指标,能够反映模型对太湖水质数据拟合的程度。从图4可见,模型训练从开始迭代到第3次迭代期间的损失迅速下降,从第3次迭代开始便很快趋于稳定,表明模型能够有效地从数据中学习规律。训练损失和验证损失之间的差距非常小,且都维持在低水平,这表明模型在训练和验证数据上都达到了良好的拟合效果,并且未出现过拟合或欠拟合的问题。此外,损失曲线的平滑性暗示了模型在学习过程中的稳定性,早停法的使用也有效避免了模型在验证集上的性能退化。
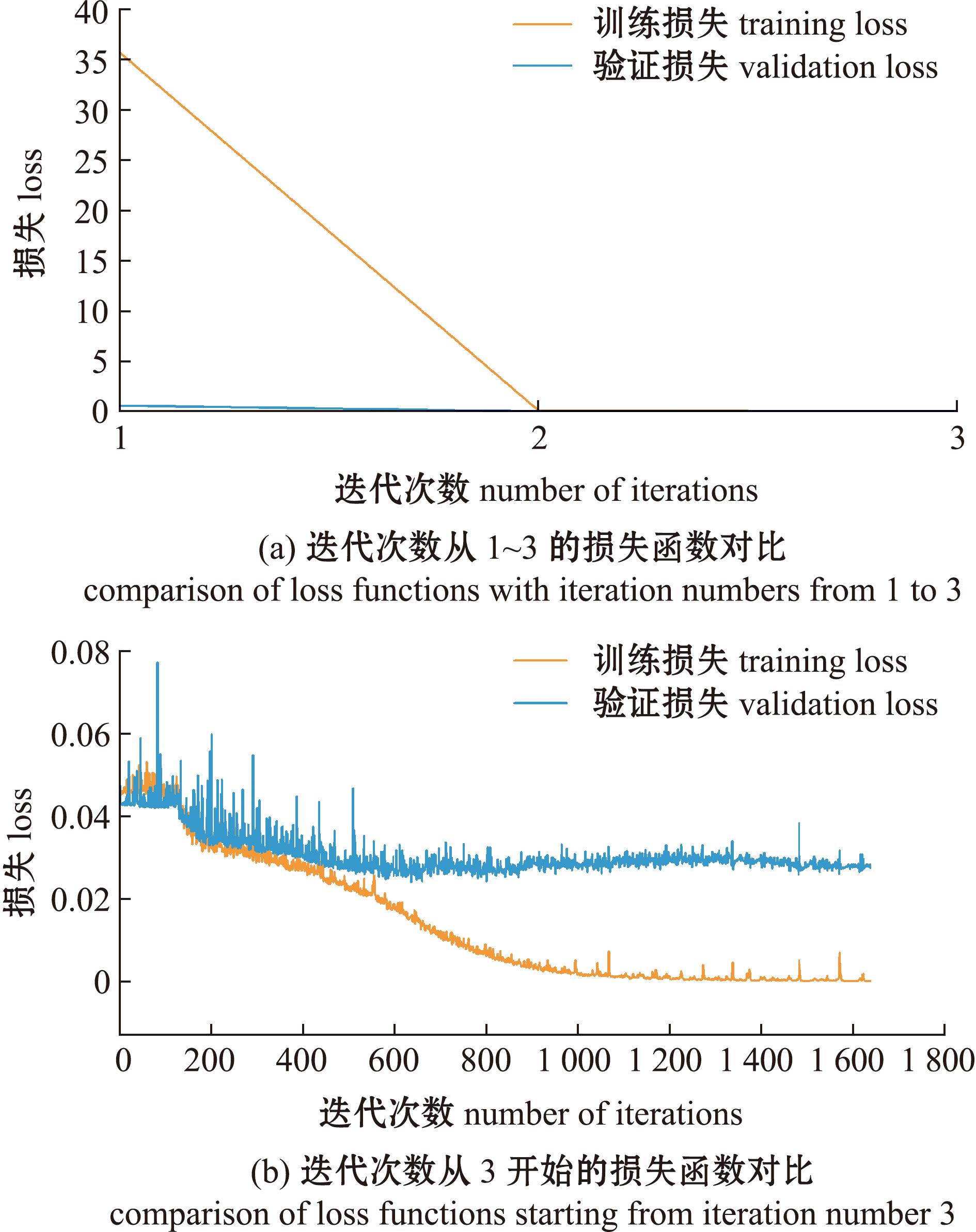
图4 模型训练中损失函数对比
Fig.4 Comparison of loss functions in model training
2.2.3 多维度试验 为了验证PELBX预测方法的准确性,本研究中对太湖水质数据进行了时间和空间两个维度的分析。
1)时间维度。在时间维度上,数据被组织成12个集合,如将2007—2015年所有1月份的数据构成一个数据集,以此类推。
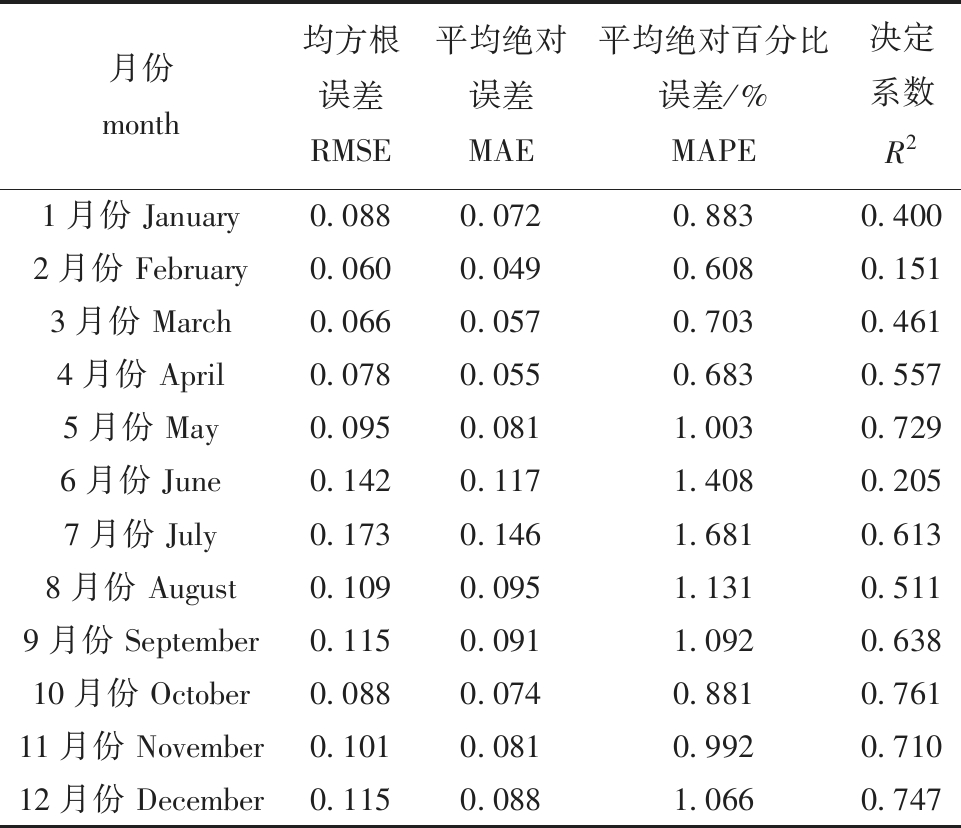
表3的试验结果显示,模型在10月的预测表现尤为出色,其均方根误差、平均绝对误差及平均绝对百分比误差均保持在较低水平,同时决定系数R2高达0.761,表明模型预测与实际测量值之间的高度一致性,试验验证了模型的高准确度。在7月这样表现一般的月份,虽然模型的预测准确度未达到最优,但其仍能够较好地反映出pH值的变化趋势,各项评价指标也处于可接受范围内。与此同时,在6月份等相对表现稍逊的月份,尽管模型预测存在一定偏差,但依然能够捕捉到pH值的主要波动方向。
表3 时间维度pH预测评价指标对比结果
Tab.3 Comparison results of pH prediction evaluation indicators in time dimension
月份month均方根误差RMSE平均绝对误差MAE平均绝对百分比误差/%MAPE决定系数R21月份 January0.0880.0720.8830.4002月份 February0.0600.0490.6080.1513月份 March0.0660.0570.7030.4614月份 April0.0780.0550.6830.5575月份 May0.0950.0811.0030.7296月份 June0.1420.1171.4080.2057月份 July0.1730.1461.6810.6138月份 August0.1090.0951.1310.5119月份 September0.1150.0911.0920.63810月份 October0.0880.0740.8810.76111月份 November0.1010.0810.9920.71012月份 December0.1150.0881.0660.747
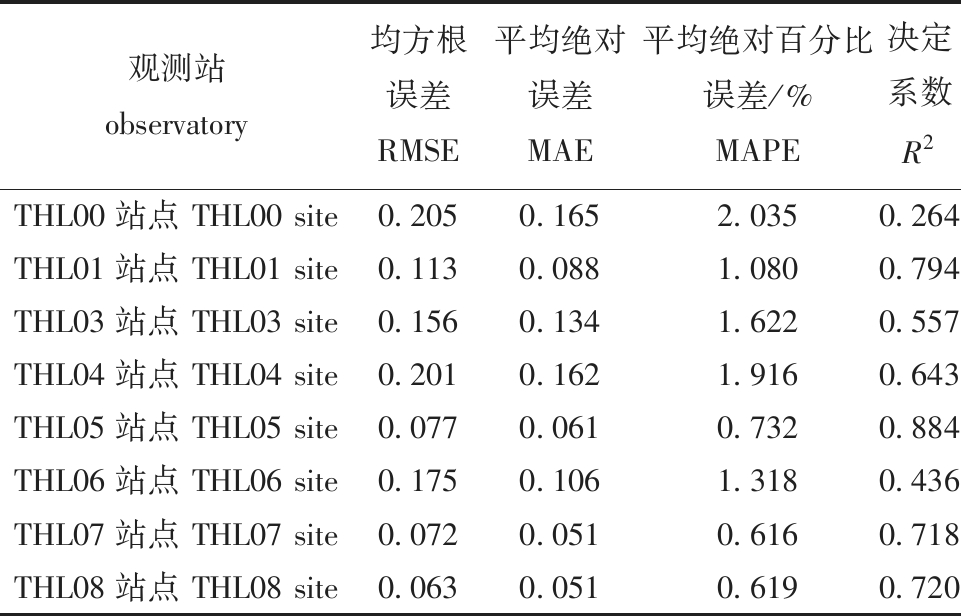
2)空间维度。在空间维度层面,本研究中对太湖2007—2015年间8个特定观测站的水质数据进行了详尽剖析。这些数据被精心划分为8个集合,每一集合均代表了一个观测站连续9年的水质监测记录。为深入评估模型在预测pH值方面的性能。经细致分析表4所呈现的对比试验结果,可见模型在各观测点的预测成果普遍表现良好。特别是在THL01、THL05、THL07及THL08观测站,模型的预测效果尤为显著,如THL05站点的均方根误差(RMSE)低至0.077,同时决定系数R2高达0.884,充分展现了其优秀的预测精度。尽管在THL00和THL04观测站,模型的预测成效相对一般,具体数据RMSE分别为0.205和0.201,R2分别为0.264和0.643,但综合来看,其预测能力仍保持在可接受水平。即便在表现稍弱的THL06站点,模型亦显示出了一定的预测准确度,其RMSE达到0.175,R2为0.436,这样的预测结果仍然具有一定的可靠性。
表4 空间维度pH预测评价指标对比结果
Tab.4 Comparison results of pH prediction evaluation indicators in spatial dimension
观测站observatory均方根误差RMSE平均绝对误差MAE平均绝对百分比误差/%MAPE决定系数R2THL00站点 THL00 site0.2050.1652.0350.264THL01站点 THL01 site0.1130.0881.0800.794THL03站点 THL03 site0.1560.1341.6220.557THL04站点 THL04 site0.2010.1621.9160.643THL05站点 THL05 site0.0770.0610.7320.884THL06站点 THL06 site0.1750.1061.3180.436THL07站点 THL07 site0.0720.0510.6160.718THL08站点 THL08 site0.0630.0510.6190.720
2.2.4 消融试验 为了验证本文提出的PELBX方法的有效性,选取了PCA-LSTM-XGBoost、PCA-LSTM-BSO-XGBoost、PCA-ES-LSTM-XGBoost、PCA-ES-LSTM、PCA-BSO-XGBoost与PELBX进行对比分析。试验过程中,所有模型均在统一的试验环境下运行,并采用了相同的试验参数设置:迭代次数设置为1 000次,每个批次处理8个样本,学习率固定在0.001。
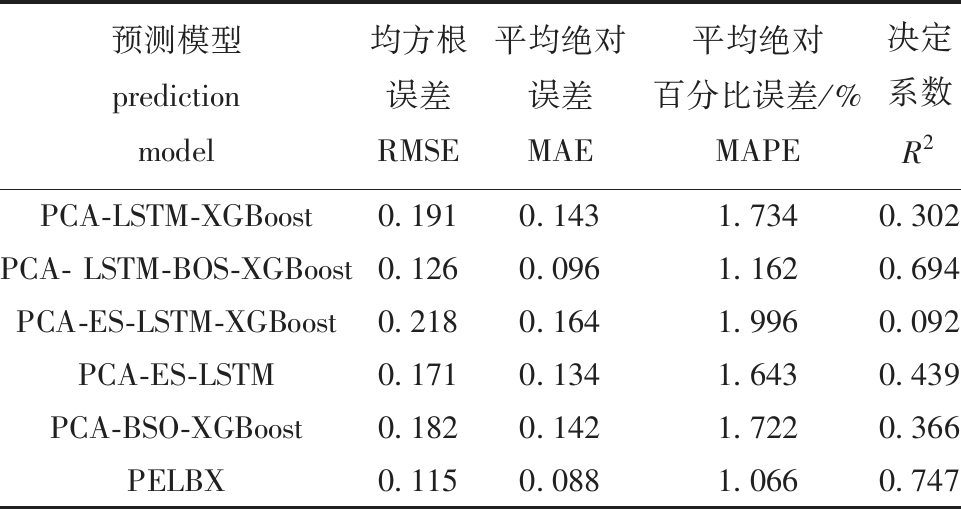
从图5可见,PELBX模型的预测曲线与实际数据曲线紧密贴合,且波动性相对较小,显示出该模型在pH值预测任务上的高准确率和稳定性。特别是在极端值和波动点上,PELBX网络模型的表现明显优于其他模型,能够更准确地捕捉数据的细微变化。从表5中则可以进一步量化地了解到,相比于试验中表现最好的PCA-LSTM-BSO-XGBoost模型,PELBX网络模型在均方根误差、平均绝对误差、平均绝对百分比误差方面分别提升了约8.73%、8.33%和8.26%,同时在决定系数上也有7.64%的提升。这些数据客观地反映了PELBX网络模型在pH值预测性能上的优越性。
表5 消融试验评价指标对比结果
Tab.5 Comparison results of evaluation indicators in ablation experiment
预测模型prediction model均方根误差RMSE平均绝对误差MAE平均绝对百分比误差/%MAPE决定系数R2PCA-LSTM-XGBoost0.1910.1431.7340.302PCA- LSTM-BOS-XGBoost0.1260.0961.1620.694PCA-ES-LSTM-XGBoost0.2180.1641.9960.092PCA-ES-LSTM0.1710.1341.6430.439PCA-BSO-XGBoost0.1820.1421.7220.366PELBX0.1150.0881.0660.747
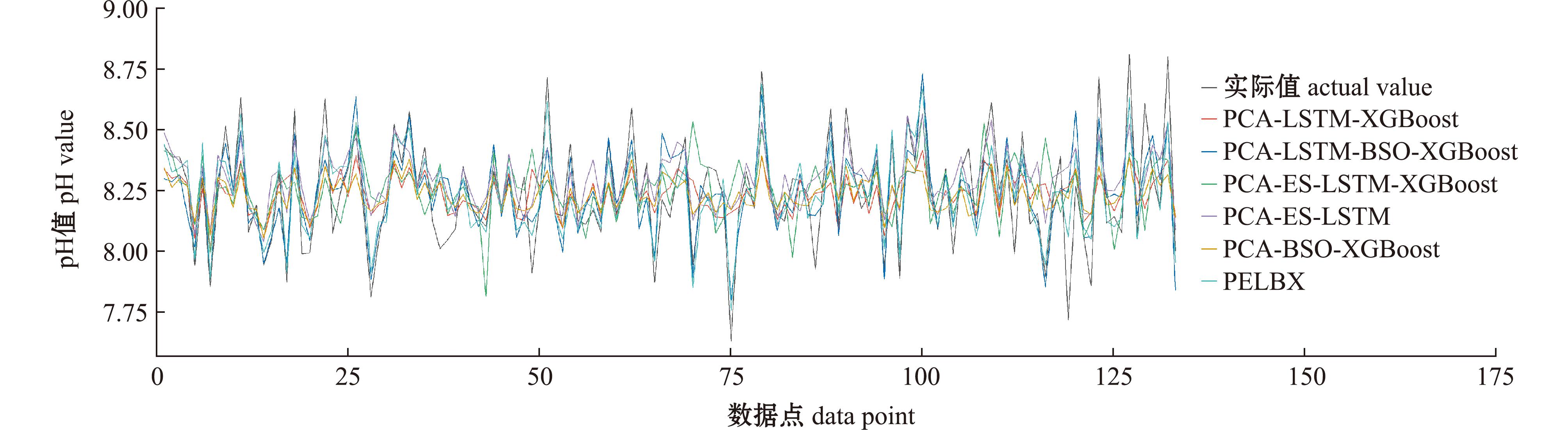
图5 实际值与各模型预测值的对比结果(消融试验结果)
Fig.5 Comparison between actual values and predicted values in each model (ablation experiment results)
2.2.5 同领域模型对比试验 为了全面评估本文所提出的PELBX网络模型在水质预测领域的综合性能,本文综合比较了其他学者在水质指标预测方面的模型,包括SAE-LSTM[11]、CNN-LSTM[16]、BiLSTM-GRU[17],以及LSTM和BiLSTM[20]。此外,为确保比较试验的全面性和客观性,还特别引入了CNN模型作为基准对照组。
从图6可见,代表PELBX预测方法的结果曲线与代表实际数据的结果曲线几乎重合,显示出其优秀的预测能力。特别是在峰值和谷值的捕捉上,PELBX模型表现出了较高的准确性。相比之下,其他模型如BiLSTM、CNN-LSTM、CNN、LSTM及SAE-LSTM,虽然在整体趋势上能与实际值保持一定程度的同步,但在极端值处却常常出现较大的波动。
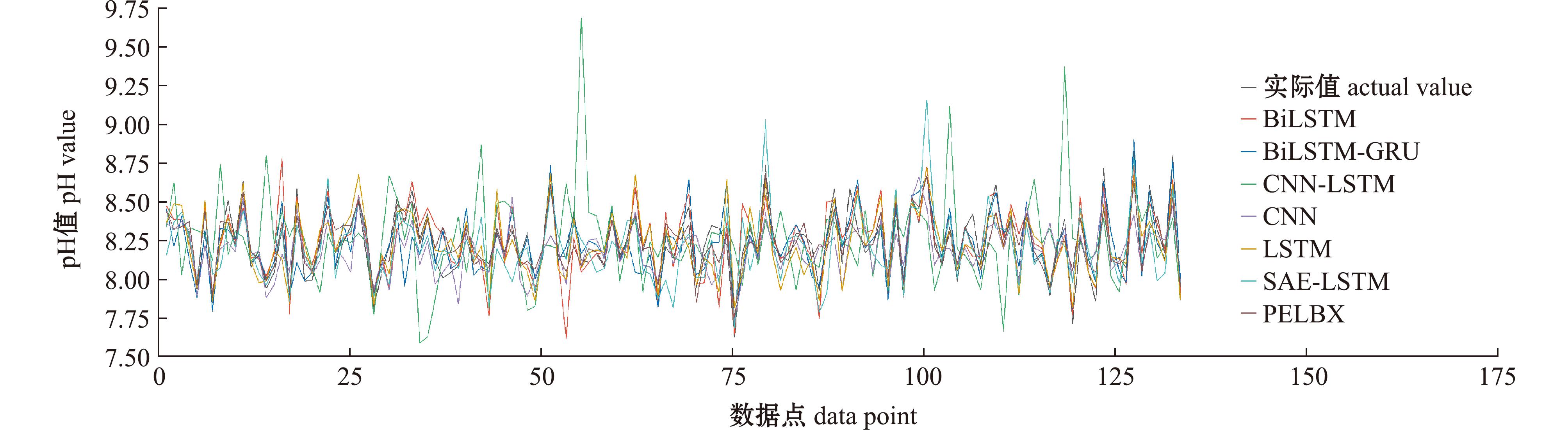
图6 实际值与各模型预测值的对比结果
Fig.6 Comparison between actual values and predicted values in each model
从表6中可以进一步确认PELBX模型的优越性。与其他模型相比,PELBX模型在均方根误差、平均绝对误差、平均绝对百分比误差和决定系数等关键指标上都表现出了显著的提升。与表现相对稳定的BiLSTM-GRU模型相比,PELBX模型在这些指标上分别提升了10.16%、1.12%、0.56%和8.73%。这些数据充分证明了PELBX模型在水质参数预测上的出色性能。
表6 对比试验结果
Tab.6 Comparative experimental results
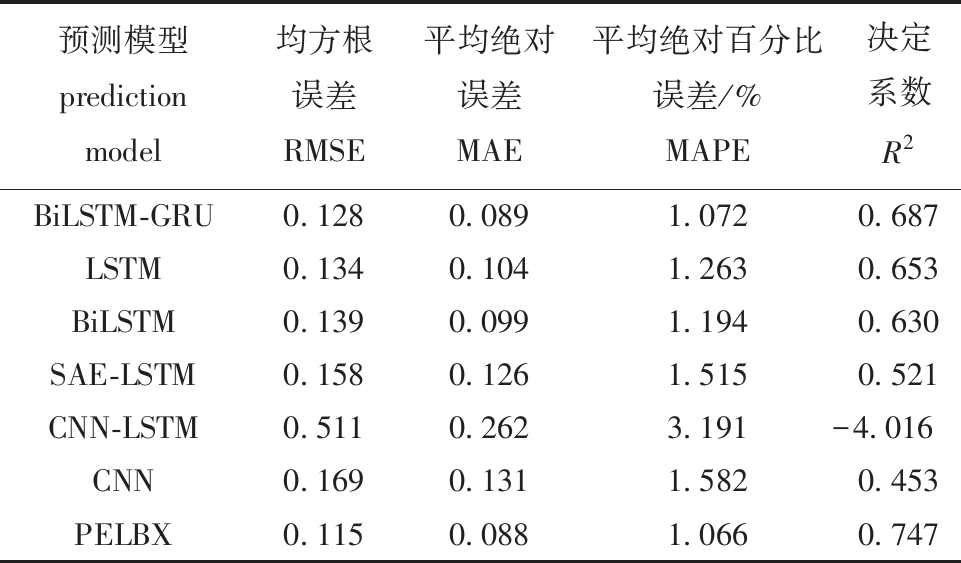
预测模型prediction model均方根误差RMSE平均绝对误差MAE平均绝对百分比误差/%MAPE决定系数R2BiLSTM-GRU0.1280.0891.0720.687LSTM0.1340.1041.2630.653BiLSTM0.1390.0991.1940.630SAE-LSTM0.1580.1261.5150.521CNN-LSTM0.5110.2623.191-4.016 CNN0.1690.1311.5820.453PELBX0.1150.0881.0660.747
3 讨论
3.1 PCA降维技术的有效性
在水质预测领域,主成分分析(PCA)作为一种高效的数据降维技术,被广泛用于减少数据维度和简化模型参数复杂性,进而提高模型训练效率和预测精度。研究表明,PCA通过正交变换将原始高维数据中的相关性变量转换为线性不相关的主成分,减少了变量数量,同时保留了数据的主要特征。如郭尚志等[23]研究展示了PCA在数据降维方面的显著效果,即便将数据降至低维空间,也能全面表达原始数据集的信息,显著降低计算量。同样,李缙等[24]也验证了PCA在油田水质评价中的有效性,通过PCA进行数据降维和特征筛选,提高了水质评价的准确性和效率。
本研究中,PCA降维技术被应用于太湖养殖水质数据的预处理阶段。通过PCA处理,原始水质参数空间被成功压缩至低维空间,同时保留了数据的主要特征。这种降维处理简化了模型参数复杂性,降低了计算复杂度,使模型能在有限计算资源下快速收敛。此外,PCA还提高了模型训练效率,减少了迭代次数,使模型更快达到稳定预测性能。
3.2 LSTM模型在时间序列分析中的优势
在水质预测领域,长短期记忆网络(LSTM)凭借其独特的结构优势,在处理时间序列数据方面展现出了显著的性能。如陈聪等[25]在发电机定子线棒出水温差的预测中采用了LSTM神经网络,通过捕捉复杂的温差变化模式,结合ARIMA模型进行修正,取得了优于单独使用LSTM或ARIMA模型的预测效果。同样,杨少毅等[26]也展示了LSTM在临近空间大气风速预测中的高精度性能,其预测精度显著超越了传统的时间序列分析方法。这些研究为LSTM在时间序列分析中的应用提供了坚实的实践基础。
在本研究中,LSTM模型发挥了至关重要的作用。它有效捕捉了太湖养殖水质参数随时间的动态变化,并通过其独特的门控机制,有效处理了时间序列数据中的长期依赖关系,从而避免了传统循环神经网络(RNN)在处理长序列时可能出现的梯度消失和梯度爆炸问题。这种优势使得LSTM模型能够精确揭示水质数据中隐藏的时间依赖关系,进而显著提高pH值预测的准确度。为了增强模型的泛化能力并防止过拟合,本研究中采用了早停法策略,通过设定验证集监控模型性能,确保模型对未见数据具有高度的预测准确性。损失函数对比试验结果显示,LSTM模型在训练过程中能够快速收敛,损失函数迅速下降并趋于稳定,这证明了LSTM模型能够从数据中高效地学习规律,并在未见数据上保持较高的预测精度。
3.3 XGBoost模型在非线性学习中的性能
在水质预测领域,XGBoost模型以其高效处理结构化数据和执行特征工程的能力,以及卓越的泛化能力,展现了出色的非线性学习能力。如陈卫东等[27]通过贝叶斯优化XGBoost算法预测小麦粉麸星含量,显著提升了预测精度。同样,姚昊天等[28]结合PCA与XGBoost,应用于洲际人群生物地理祖源推断,验证了该模型的高准确率和良好的泛化能力。缪季等[29]在建筑施工事故类型预测中也展示了结合特征选择算法和贝叶斯优化XGBoost模型的优越性能。这些研究充分展现了XGBoost模型在非线性学习中的强大潜力。
在本研究中,XGBoost模型被用于预测pH值变化率,并通过贝叶斯优化算法对模型参数进行了精细调整。这种优化策略显著提升了XGBoost模型在非线性学习中的性能,使其能够更好地探索数据中的复杂关系,从而提高了pH值预测的准确性和稳定性。消融试验的结果表明,经过优化的PCA-LSTM-BSO-XGBoost模型在各项性能指标上均优于未经优化的PCA-LSTM-XGBoost模型,其在均方根误差、平均绝对误差和平均绝对百分比误差等关键指标上均有显著提升(表5)。这些结果进一步证明了XGBoost模型在非线性学习中的优势,为水质预测领域提供了新的解决方案。
3.4 集成模型的优势
通过将LSTM和XGBoost模型的预测结果进行加权集成,本研究中的PELBX模型成功融合了时间序列分析与非线性学习的优势,显著提高了养殖水质pH值的预测准确性。这种集成策略有效地弥补了单一模型在处理复杂数据结构时的不足,并充分利用了不同模型各自的优点,实现了更为精准的预测。如赵阳等[30]在电量预测中采用的智能加权混合模型,以及杨霞等[31]在红外时间序列预测中提出的Prophet与SARIMA动态加权组合模型,均证明集成模型在复杂系统预测中展现出显著的优势,不仅提高了预测精度,还增强了模型的鲁棒性。
在本研究中,LSTM模型利用其独特的门控机制,精确捕捉了水质参数随时间变化的动态特性,有效处理了时间序列数据中的长期依赖关系。同时,XGBoost模型凭借其在处理结构化数据和执行特征工程方面的高效性及卓越的泛化能力,为pH值预测提供了强有力的支持。通过将LSTM和XGBoost模型的预测结果进行加权集成,PELBX模型结合了时间序列分析与非线性学习的优点,克服了单一模型在处理复杂数据结构时的局限性。
4 结论
针对太湖水质的复杂情况,本研究中构建的PELBX网络模型融合了主成分分析的数据降维技术、LSTM的时间序列分析能力、贝叶斯算法的参数优化机制和XGBoost的高效预测性能,形成了一个高度集成化的水质预测模型。通过对模型进行全面的性能评估,得出以下结论。
1)经过高斯滤波平滑、Z-score异常值处理和PCA降维后,模型在均方根误差、平均绝对误差、平均绝对百分比误差和决定系数(R2)等关键性能指标上显著优于传统方法,证明了其在处理复杂水质数据上的高效性和准确性。
2)通过贝叶斯优化算法进一步增强了模型的预测能力,特别是在预测太湖水质pH值方面表现出明显的优势,为水质管理提供了有力的支持。
3)模型预测结果与实际测量值高度一致,展示了模型在追踪水质变化趋势上的高精度。相比其他对比模型,其在多项性能评价指标上的表现凸显了PELBX网络模型的创新性和实用价值。
基于本研究成果,未来工作将集中于提高模型的精度与泛化能力,具体包括采用更先进的算法及融合额外的环境因素(如气候和人类活动)以增强预测性能。
[1] 张宏伟,高健,刘依阳.太湖捕捞渔业现状及其可持续发展对策的探析[J].中国水产,2016(12):34-36.
ZHANG H W,GAO J,LIU Y Y.Analysis on the current situation of fishing and fishery in Taihu Lake and its sustainable development countermeasures[J].China Fisheries,2016(12):34-36.(in Chinese)
[2] 周小燕,吕占民,杨雨琦.2022年水产养殖机械化进展情况[J].农机科技推广,2023(1):22-24.
ZHOU X Y,LÜ Z M,YANG Y Q.Progress of aquaculture mechanization in 2022[J].Agriculture Machinery Technology Extension,2023(1):22-24.(in Chinese)
[3] 籍淑芳,李晨,韩朋利,等.基于统计学方法的北京昌平区地下水质分析[J].北京水务,2023(2):45-50.
JI S F,LI C,HAN P L,et al.Analysis of groundwater quality in Changping District of Beijing based on statistical methods[J].Beijing Water,2023(2):45-50.(in Chinese)
[4] 李婉君,许惠燕,梁建霞,等.基于多准则统计学方法的珠三角区域地表水水质监测及评价[J].云南化工,2022,49(10):100-104.
LI W J,XU H Y,LIANG J X,et al.Monitoring and evaluation of surface water quality in Pearl River Delta Region based on multi-criteria statistical method[J].Yunnan Chemical Technology,2022,49(10):100-104.(in Chinese)
[5] 万蕾,孙晓虎.云龙湖水质状况统计学分析[J].苏州科技大学学报(工程技术版),2020,33(4):41-46,52.
WAN L,SUN X H.Statistical analysis of water quality change in Yunlong Lake[J].Journal of Suzhou University of Science and Technology(Engineering and Technology Edition),2020,33(4):41-46,52.(in Chinese)
[6] 张稳.某化肥企业污水处理站主要水质指标及处理效果的统计学分析[D].合肥:安徽农业大学,2020.
ZHANG W.Statistical analysis on main water quality index and treatment efficiency of wastewater treatment station in a fertilizer enterprise[D].Hefei:Anhui Agricultural University,2020.(in Chinese)
[7] GALOIE M,MOTAMEDI A,FAN J H,et al.Prediction of water quality under the impacts of fine dust and sand storm events using an experimental model and multivariate regression analysis[J].Environmental Pollution,2023,336:122462.
[8] WANG Z C,WANG Q Y,WU T.A novel hybrid model for water quality prediction based on VMD and IGOA optimized for LSTM[J].Frontiers of Environmental Science &Engineering,2023,17(7):88.
[9] RAHUL GANDH D,RASHEED ABDUL HAQ K P,HARIGOVINDAN V P,et al.LSTM and GRU based accurate water quality prediction for smart aquaculture[J].Journal of Physics:Conference Series,2023,2466(1):012027.
[10] BI J,ZHANG L Y,YUAN H T,et al.Multi-indicator water quality prediction with attention-assisted bidirectional LSTM and encoder-decoder[J].Information Sciences,2023,625:65-80.
[11] 李彦杰,贺鹏飞,冯巍巍,等.基于LSTM模型的海洋水质预测[J].计算机与数字工程,2020,48(2):437-441.
LI Y J,HE P F,FENG W W,et al.Marine water quality prediction based on LSTM model[J].Computer &Digital Engineering,2020,48(2):437-441.(in Chinese)
[12] 顾乾晖,涂振宇,杨昊天,等.基于QPSO优化LSTM神经网络水质预测模型的应用研究[J].网络安全技术与应用,2021(5):42-45.
GU Q H,TU Z Y,YANG H T,et al.Application research of LSTM neural network water quality prediction model based on QPSO optimization[J].Network Security Technology &Application,2021(5):42-45.(in Chinese)
[13] GAO Z Y,CHEN J Y,WANG G Q,et al.A novel multivariate time series prediction of crucial water quality parameters with Long Short-Term Memory (LSTM) networks[J].Journal of Contaminant Hydrology,2023,259:104262.
[14] ZHANG Y T,LI C L,JIANG Y Q,et al.Accurate prediction of water quality in urban drainage network with integrated EMD-LSTM model[J].Journal of Cleaner Production,2022,354:131724.
[15] RASHEED ABDUL HAQ K P,HARIGOVINDAN V P.Water quality prediction for smart aquaculture using hybrid deep learning models[J].IEEE Access,2022,10:60078-60098.
[16] ZHANG W Y,ZHOU H Y,BAO X H,et al.Outlet water temperature prediction of energy pile based on spatial-temporal feature extraction through CNN-LSTM hybrid model[J].Energy,2023,264:126190.
[17] 石庆兰,束金阳,李道亮,等.基于BiLSTM-GRU融合网络的稻虾养殖溶解氧含量预测[J].农业机械学报,2023,54(10):364-370.
SHI Q L,SHU J Y,LI D L,et al.Dissolved oxygen prediction in rice and shrimp culture based on BiLSTM-GRU fusion neural networks[J].Transactions of the Chinese Society for Agricultural Machinery,2023,54(10):364-370.(in Chinese)
[18] CHEN L X,WU T,WANG Z C,et al.A novel hybrid BPNN model based on adaptive evolutionary Artificial Bee Colony Algorithm for water quality index prediction[J].Ecological Indicators,2023,146:109882.
[19] TIAN Q Q,LUO W,GUO L.Water quality prediction in the Yellow River source area based on the DeepTCN-GRU model[J].Journal of Water Process Engineering,2024,59:105052.
[20] GUO Y,ZHANG L F,HE Y,et al.LSTM time series NDVI prediction method incorporating climate elements:a case study of Yellow River Basin,China[J].Journal of Hydrology,2024,629:130518.
[21] 张雪薇,韩震.基于ConvGRU深度学习网络模型的海表面温度预测[J].大连海洋大学学报,2022,37(3):531-538.
ZHANG X W,HAN Z.Prediction of sea surface temperature based on ConvGRU deep learning network model[J].Journal of Dalian Ocean University,2022,37(3):531-538.(in Chinese)
[22] AGGARWAL C C.Data mining:the textbook[M].New York:Springer,2015.
[23] 郭尚志,廖晓峰,李刚,等.基于PCA的大数据降维应用[J].计算机仿真,2024,41(5):483-486.
GUO S Z,LIAO X F,LI G,et al.Dimensionality reduction application of big data based on PCA[J].Computer Simulation,2024,41(5):483-486.(in Chinese)
[24] 李缙,王平,谢鸣,等.基于PCA-GRA-TOPSIS法的注水水质评价方法研究[J].油气田地面工程,2022,41(5):46-51.
LI J,WANG P,XIE M,et al.Study on evaluation method of injection water quality based on PCA-GRA-TOPSIS method[J].Oil-Gas Field Surface Engineering,2022,41(5):46-51.(in Chinese)
[25] 陈聪,王晓剑,徐俊元,等.基于LSTM-ARIMA算法的发电机定子线棒出水温差预测[J].大电机技术,2023(5):43-48.
CHEN C,WANG X J,XU J Y,et al.Prediction of outlet-water temperature difference of generator stator bars based on LSTM-ARIMA algorithm[J].Large Electric Machine and Hydraulic Turbine,2023(5):43-48.(in Chinese)
[26] 杨少毅,李娜,丁宗华,等.基于LSTM神经网络的临近空间大气风速预测方法研究[C]//第十七届全国电波传播年会会议论文集.延安:中国电子学会电波传播分会.2022:4.DOI:10.26914/c.cnkihy.2022.035604.
LIU S Y,LI N,DING Z H,et al.Prediction method of atmospheric wind speed in near space based on LSTM neural network[C]//Proceedings of the 17th National Annual Conference on Radio Propagation Society.Yan’an:Radio Propagation Society of Chinese Institute of Electronics.2022:4.DOI:10.26914/c.cnkihy.2022.035604.(in Chinese)
[27] 陈卫东,刘超,范冰冰,等.基于贝叶斯优化XGBoost的小麦粉麸星含量预测[J/OL].河南工业大学学报(自然科学版):1-14[2024-06-23].https://doi.org/10.16433/j.1673-2383.202401200001.
CHEN W D,LIU C,FAN B B,et al.Prediction of bran speck content in wheat flour based on XGBoost with Bayesian optimization[J/OL].Journal of Henan University of Technology(Natural Science Edition):1-14[2024-06-23].https://doi.org/10.16433/j.1673-2383.202401200001.(in Chinese)
[28] 姚昊天,江丽,王春年,等.基于PCA-XGBoost方法的洲际人群生物地理祖源推断模型研究[J/OL].生物化学与生物物理进展:1-19[2024-06-23].https://doi.org/10.16476/j.pibb.2023.0453.
YAO H T,JIANG L,WANG C N,et al.Research on the intercontinental population biogeographic ancestral inference model based on PCA-XGBoost method [J/OL].Progress in Biochemistry and Biophysics:1-19[2024-06-23].https://doi.org/10.16476/j.pibb.2023.0453.(in Chinese)
[29] 缪季,段立平,刘吉明,等.基于贝叶斯优化XGBoost的建筑施工事故类型预测[J].中国安全生产科学技术,2024,20(5):57-63.
MIAO J,DUAN L P,LIU J M,et al.Prediction on accident types of building construction based on Bayesian optimized XGBoost[J].Journal of Safety Science and Technology,2024,20(5):57-63.(in Chinese)
[30] 赵阳,范文奕,安佳坤,等.基于智能加权混合模型的新型电力系统电量预测方法[J].电测与仪表,2022,59(12):56-63.
ZHAO Y,FAN W Y,AN J K,et al.A method of novel power system electricity forecasting based on intelligent weighted hybrid model[J].Electrical Measurement &Instrumentation,2022,59(12):56-63.(in Chinese)
[31] 杨霞,袁丁,严清,等.基于加权组合模型的红外时间序列预测[J].计算机工程与设计,2021,42(11):3076-3083.
YANG X,YUAN D,YAN Q,et al.Infrared time series forecasting based on weighted combination model[J].Computer Engineering and Design,2021,42(11):3076-3083.(in Chinese)