浮式防波堤具有安装方便、可进行水质交换、可在不同环境下建造及可移动等优点,是近年来研究和应用比较广泛的防波堤类型[1]。同时在推进实现全球碳中和的背景下,波浪能被认为是最佳的清洁能源之一。因此,研发具有较好的消浪性能并可兼顾波浪能发电等多种功能的浮式防波堤具有相当重要的应用价值及现实意义。
研究发现,双体浮式防波堤结构具有更好的消浪特性,近年来,国内外学者们对双体浮式防波堤进行了大量的数值模拟研究[2-6]和试验研究[7-9],先后讨论了浮堤宽度、间距、水深、周期和锚链刚度等因素对透射系数和反射系数的影响。而对于浮式防波堤开孔方面的研究,多位学者[10-12]讨论了不同的结构参数、孔隙率等因素对多孔浮式防波堤消浪性能及系泊受力的影响。开孔有利于波浪充分掺杂破碎,有效减小透射系数,并增强消浪效果。此外,在波浪能开发装置中,振荡水柱式(OWC)波浪能发电装置应用较广,其工作原理是利用波浪上下浮动引起腔体内部的水面不断起伏,内部空气被挤压,通过排气口设置透平装置发电。近年来,研究者对OWC发电装置的研究从小型到大型,从近岸式转变为离岸式,从浅海转变为深海,为OWC与浮式防波堤的结合奠定了基础[13]。基于此基础,国内外学者[14-21]先后对振荡水柱装置与防波堤结合的结构进行研究,讨论了消波效果及其对波浪能的吸收与耗散能力等情况。
综上可知,研究人员已对双体浮式防波堤、开孔浮堤、浮堤与发电装置结合的结构有了初步了解,李佳繁等[18]针对OWC振荡水柱装置与开孔方箱相结合的双体浮式防波堤的消浪性能进行了讨论,其中,浮堤迎浪侧方箱中嵌入OWC装置,背浪侧方箱采用开孔结构,本研究中主要针对浮堤的稳定性基于ANSYS AQWA软件展开数值研究,讨论双箱间距、开口宽度和锚泊方式等因素对浮堤运动幅度的影响规律,探讨浮堤的固有频率,避免发生共振现象,以期为多功能浮式防波堤的实际工程应用提供科学参考。
1 计算模型
1.1 模型结构
OWC-开孔浮式防波堤主要有两个方浮箱(图1),这种组合结构形式旨在消减波浪的同时利用波浪能。迎浪侧为嵌入OWC的方箱,背浪侧为开孔方箱,顶部和两侧的小孔尺寸分别为0.5 m×0.8 m和0.5 m×0.5 m,开孔率为16.7%。单个方箱的尺寸为18 m×12 m×8 m,吃水深度为5 m,两方箱用挡板相连,间距为d,各部分构件之间刚性连接。锚链采用八字锚泊方式,锚链总长为45 m,拖地长度为l,系泊浮堤示意图如图2所示,浮堤上部结构尺寸如图3所示。

图1 OWC-开孔浮式防波堤上部结构模型示意图
Fig.1 Schematic diagram of upper structure model of OWC-perforated floating breakwater
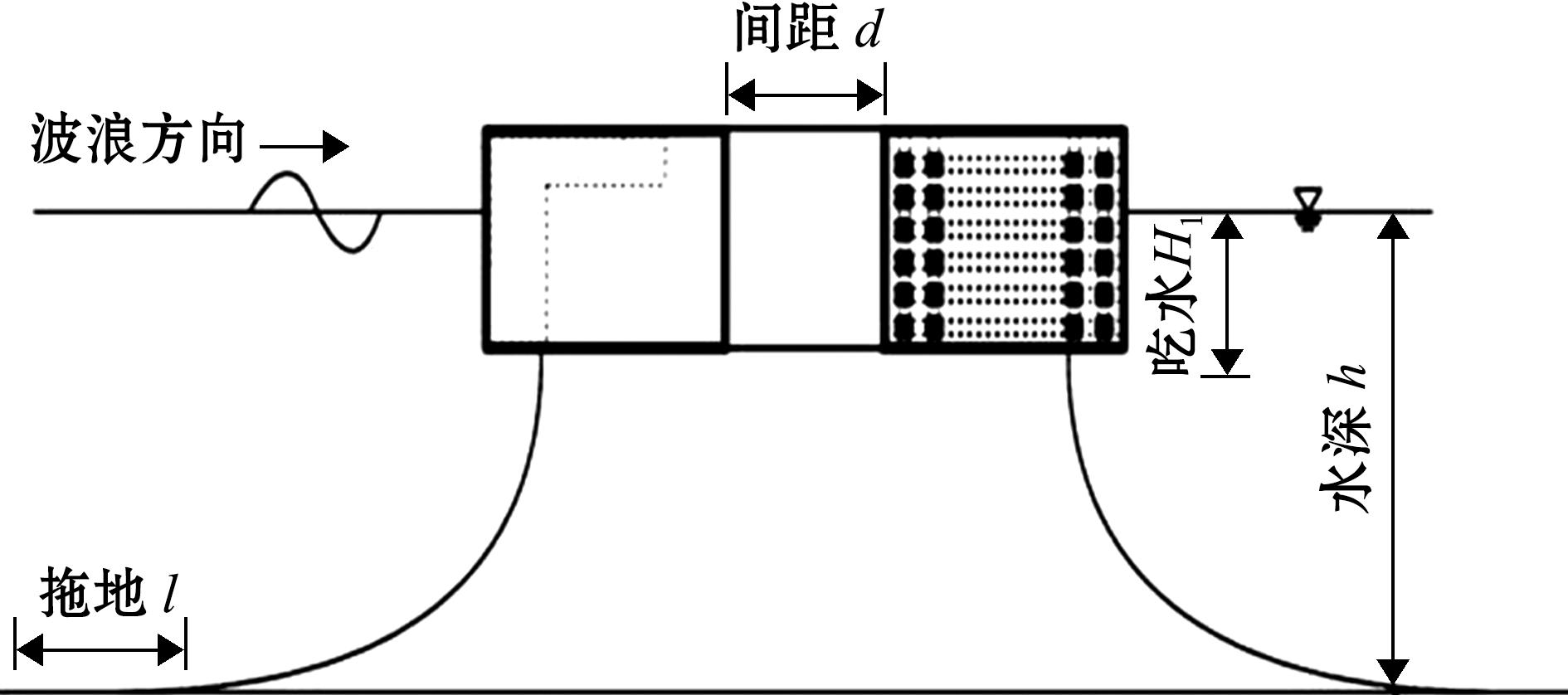
图2 锚链系泊OWC-开孔浮式防波堤示意图
Fig.2 Schematic diagram of anchor chain mooring of OWC-perforated floating breakwater
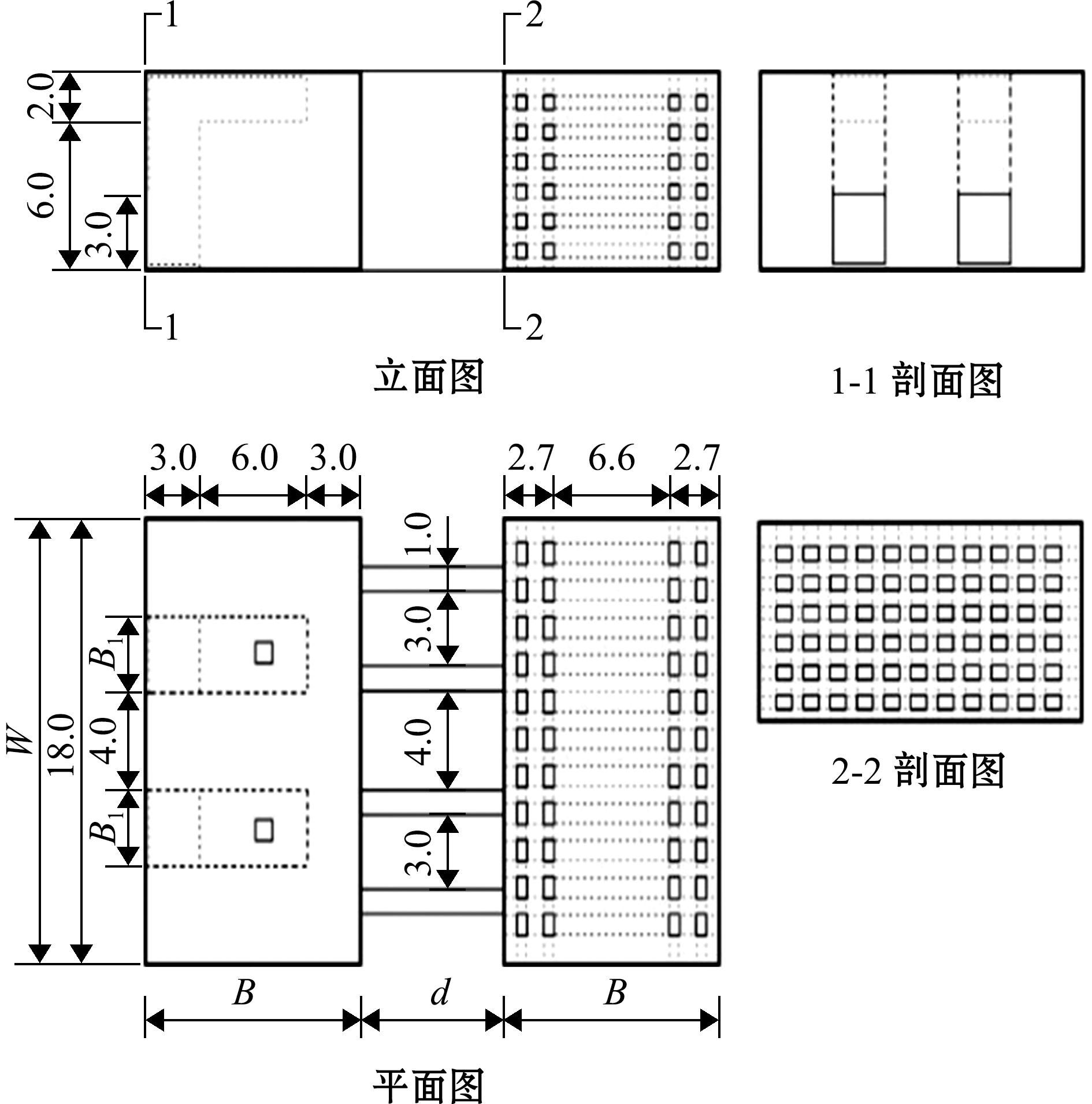
图3 OWC-开孔浮式防波堤上部结构尺寸图(m)
Fig.3 Dimensional drawing of upper structure of OWC-perforated floating breakwater (m)
1.2 模拟条件
数值模拟波浪采用规则波,具体计算工况见表1,锚链参数见表2。
表1 计算工况
Tab.1 Calculation conditions

参数 parameter内容 content参数 parameter内容 content锚泊方式 anchorage mode八字锚泊open mooring波高 height of wave(H)/m1、3、5水深 depth of water(h)/m18、25间距 distance(d)/m6、8、10、12OWC开口宽度 opening width of OWC(B1)/m3、5波浪周期 interval(T)/s5.00、5.82、6.95、8.63、11.40、15.00波浪入射角 wave incidence/(°)0、30、45、60
表2 锚链参数
Tab.2 Chain parameters

锚链参数chain parameter单位长度锚链质量/(kg·m-1)weight of cable per unit length等效截面/m2equivalent cross section刚度/kNstiffness最大张力/kNmaximum tension数值4050.377 3006 890
2 数值建模
2.1 应用软件
应用ANSYS AQWA软件,基于三维势流理论,利用Rhino创建浮体结构实体模型,读入ANSYS Workbench中,对其修正后将水面以下的结构划分若干网格进行计算。主要应用Hydrodynamic Diffraction模块和Hydrodynamic Response模块。利用频域水动力求解模块(HD模块),可以模拟浮式防波堤在规则波中的运动响应,在Solution中进行静水力计算和水动力计算,在Results中进行幅值响应算子的结果输出。
2.2 控制方程及边界条件
假定流体为不可压缩的均匀理想流体,流场速度势的控制方程为Laplace方程:
 2φ=0。
2φ=0。
(1)
运用线性叠加原理,简谐传播的波浪中具有浮动刚体的流场速度势,计算公式为
φ(x,y,x,t)=φr+φw+φd
。
(2)
式中:φr为浮体运动产生的辐射势;φw为波浪未经浮体扰动的入射势;φd为波浪穿过浮体产生的绕射势。
由物质导数和伯努利方程推导可得,自由表面运动学和动力学边界条件为
dX/dt= φ,
φ,
(3)
(4)
式中:d/dt=∂/∂t+ φ×
φ× φ为物质导数;X(x,y,z)为瞬时自由水面流体任意质点的位置矢量;η为自由水面高程;g为重力加速度。
φ为物质导数;X(x,y,z)为瞬时自由水面流体任意质点的位置矢量;η为自由水面高程;g为重力加速度。
海底边界条件为
∂φ/∂z=0,z=-h。
(5)
物体表面条件为假设物体表面是不可穿透的固体壁面,表面上任意一点的法方向i速度等于紧贴该表面的流体质点的法向速度。
 φ×n|s=U×n。
φ×n|s=U×n。
(6)
式中:U为质点运动速度;n为物体表面的法向量。
无穷远处的自由表面会产生波浪辐射,在三维计算域的无穷远处,其计算公式为
(7)
2.3 幅值响应算子
根据牛顿第二定律建立浮体运动方程,频率为ω的入射波作用下浮体的运动矢量表达式[22]为
ξ(ω)=[-ω2{M+A(ω)}-iωD+C]-1F(w)。
(8)
式中:M为惯性力矩阵;A为附加质量矩阵;C为静水回复力刚度;D为阻尼矩阵;F(ω)为流体作用力,ξ(ω)为浮体的运动响应幅值。
单位波幅的入射波作用得到的运动响应称为幅值响应算子(response amplitude operator,RAO),记为
RAO(ω)=ξ(ω)/ζ。
(9)
式中:ζ为入射波波幅。
2.4 模型验证
为验证本文数学模型计算的准确性,对浮堤的运动幅值进行计算,将RAO结果与文献[23]结果进行比较。图4给出了双浮箱-双水平板浮式防波堤示意图,图5分别为垂荡、纵摇和横摇运动的结果,与文献结果比较可以看出,二者吻合较好。
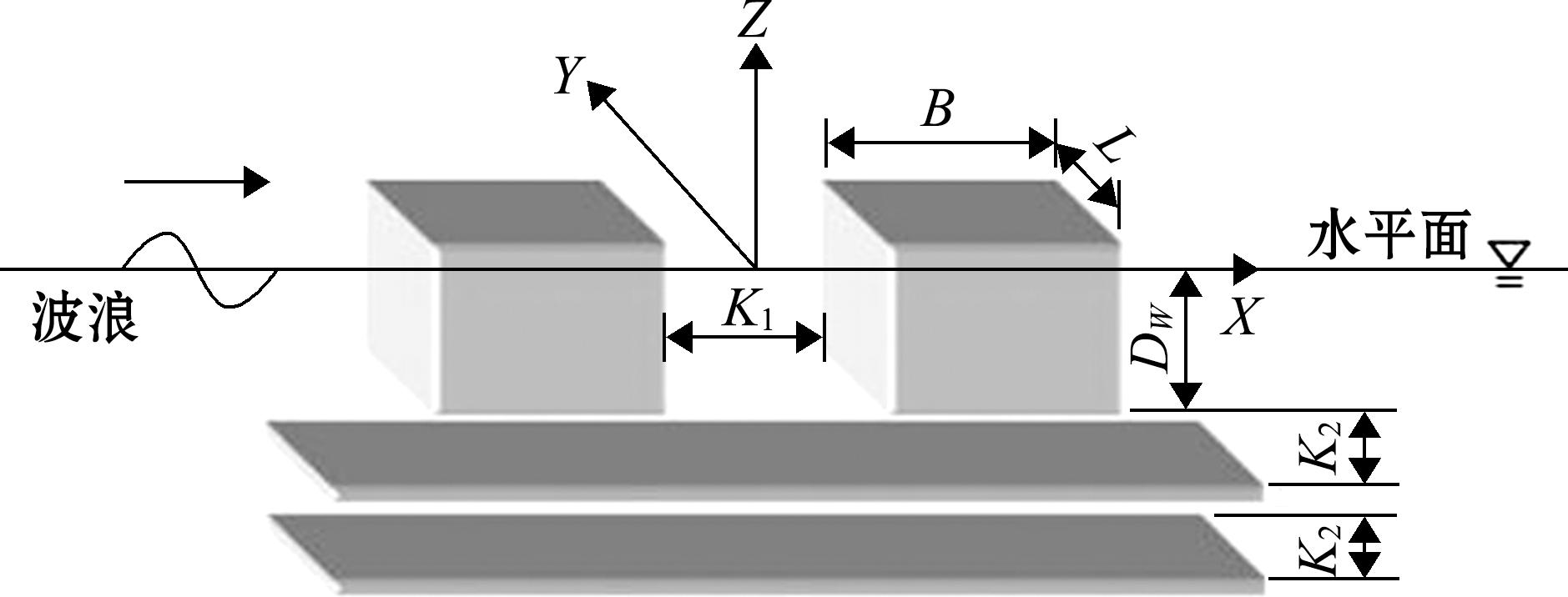
图4 双浮箱-双水平板浮式防波堤示意图
Fig.4 Schematic diagram of double-box floating breakwater with double horizontal plates

图5 双浮箱-双水平板浮堤幅值响应算子验证
Fig.5 RAO verification of double-box floating breakwater with double horizontal plates
3 数值模拟结果分析
3.1 结构形式对稳定性的影响
浮式防波堤的系泊稳定性分析主要是指浮体运动幅值响应算子(RAO),表明在线性波浪作用下浮体的运动响应特征。本研究中建立了4种结构相似的浮式防波堤进行模拟,A、B、C和D共4个模型分别是双方箱浮式防波堤、OWC方箱-方箱浮式防波堤、方箱-开孔方箱浮式防波堤及嵌入OWC方箱-开孔方箱浮式防波堤,浮堤的上部结构及示意图见表3。4种结构的锚泊方式都采用八字锚泊,锚链拖地长度为9 m,水深为25 m。设置双体间距为6 m,结构吃水深度为5 m,OWC开口宽度为3 m。
表3 浮堤上部结构模型
Tab.3 Upper structure model of floating embankment
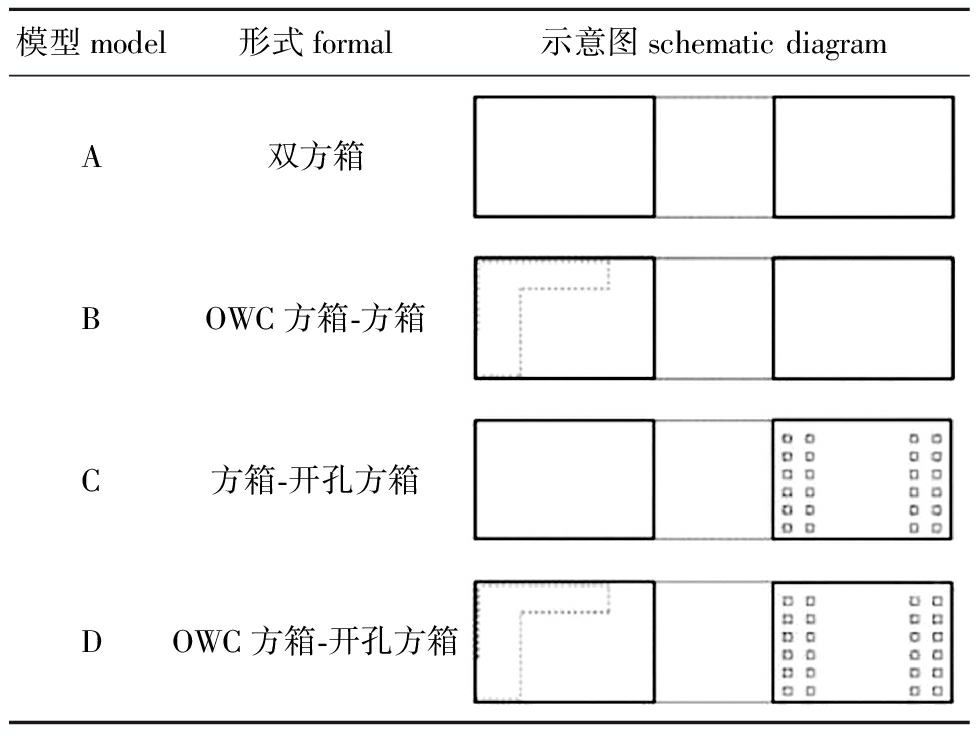
模型model形式formal 示意图schematic diagramA双方箱BOWC方箱-方箱C方箱-开孔方箱DOWC方箱-开孔方箱
通过对4种不同模型结构的模拟,图6给出了4种相似结构(模型 A、模型 B、模型 C和模型 D)在相同工况条件下的垂荡、纵摇及横摇的RAO随波浪周期的变化曲线。
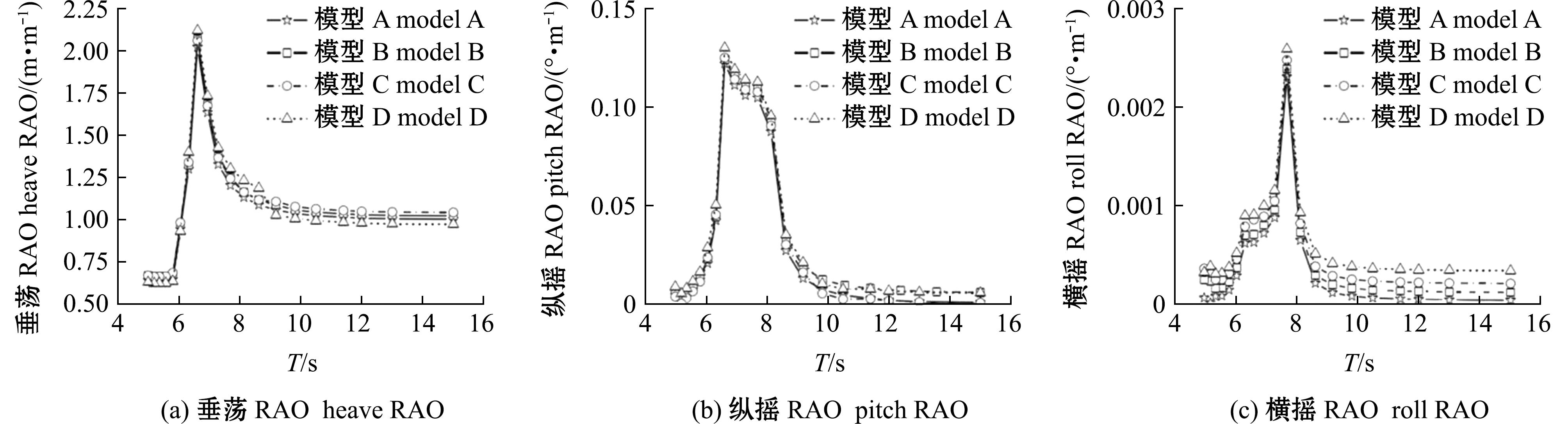
图6 4种不同模型结构的幅值响应算子
Fig.6 RAOs for four different model structures
从图6可见,4种结构的运动幅值响应算子变化趋势基本相同,尤其是在纵摇及垂荡方向,在横摇方向上模型D的运动幅值响应算子略高于其他3种相似结构,这是由于模型D是由嵌入OWC装置的方箱及多孔方箱组成的,由于方箱都采取开孔结构,导致OWC-开孔双体浮式防波堤的重心略微上移,略高于模型A、模型B和模型C,所以其运动幅值响应算子会略微增大,当波浪进入OWC装置内部时,也会使嵌入OWC装置的前方箱产生微小晃动,使其横摇方向的运动幅值响应算子有一些浮动变化。
因此,在设计该类型的结构模型时,要充分考虑横摇方向的运动幅值响应算子对其影响,以免对模型产生破坏作用。另外,从图6可见,运动幅值响应算子取峰值时对应的周期即为OWC-开孔双体浮式防波堤的固有周期,此时固有周期为6.62 s,当浮堤所在位置的波浪频率与其固有周期很接近时会使浮堤产生剧烈震动,使运动幅值大幅度增大,结构极易发生损坏。
3.2 入射波角度对稳定性的影响
为了研究入射波角度对垂荡方向运动响应的影响,选取双体间为10 m,结构吃水深度为5 m,OWC开口宽度为3 m,海水深度为25 m条件下进行模拟,可以得到其垂荡、纵摇运动幅值响应算子曲线如图7所示。4条曲线对应θ分别为0°、30°、45°、60°。

图7 不同入射角度下的幅值响应算子
Fig.7 RAOs at different incident angles
从图7(a)可见,垂荡方向上不同波浪入射角度运动曲线基本重合,这说明波浪入射角度对垂荡运动的运动幅值响应算子影响不大。在纵摇方向上,从图7(b)可见,不同入射角下运动幅值响应算子在周期为6.62 s左右时达到峰值,当周期大于6.62 s时,运动幅值响应算子随波浪周期的增大反而减小;在周期相同情况下,入射角为0°时运动幅值响应算子最大,入射角为60°时运动幅值响应算子最小。这是由于当波浪入射角较小时,波浪基本为正向入射,进入OWC装置内部的波浪能量更加集中,波浪对OWC-开孔双体浮式防波堤的冲击作用更大;随着入射波角度的增大,进入OWC装置内部的波浪能量减小,导致整个结构的纵摇方向运动幅值响应算子减小。
3.3 双体间距对稳定性的影响
为研究双体间距对系统锚泊稳定性的影响,选取海水深度为25 m,OWC开口宽度为3 m,模拟双体间距为8、10、12 m(对应d/B分别为0.75、0.83、1.00)条件下的运动幅值响应算子,可以得到垂荡、纵摇及横摇的结果分别如图8所示。3条曲线分别对应d/B分别为0.75、0.83、1.00。

图8 不同间距情况下的幅值响应算子
Fig.8 RAOs under different spacing conditions
从图8可见,3条曲线的趋势基本相同,数值相差基本不大,说明双体间距的改变对结构的运动幅值响应算子的影响不是很明显,尤其是在横摇方向上。由此可知,OWC-开孔双体浮式防波堤组合双体结构间距的改变对结构的系泊稳定性无明显影响。
3.4 OWC开口宽度对稳定性的影响
为了研究浮堤OWC开口宽度对系统锚泊稳定性的影响,本研究中选取海水深度为25 m,双体间距为10 m,选取两种OWC开口宽度为3、5 m,对其进行模拟,可以得到垂荡、纵摇及横摇的运动幅值响应算子分别如图9所示。两条曲线分别对应吃水深度为3、5 m。从图9可见,开口宽度对OWC-开孔双体浮式防波堤的运动幅值响应算子的影响比较明显,但两者趋势基本相同,在达到幅值后开始逐渐减小;随着OWC开口宽度的增大,运动幅值响应算子也随之增加,尤其是纵摇方向,最大差值可以达到0.041。这是由于当改变OWC开口宽度,结构的重心位置也会随之改变,OWC开口宽度越宽,重心位置越高,运动幅值响应算子越大。当OWC开口宽度增大时,进入OWC装置内部的波浪增多,波浪对浮堤正向的冲击增大,对纵摇的影响相应增大。
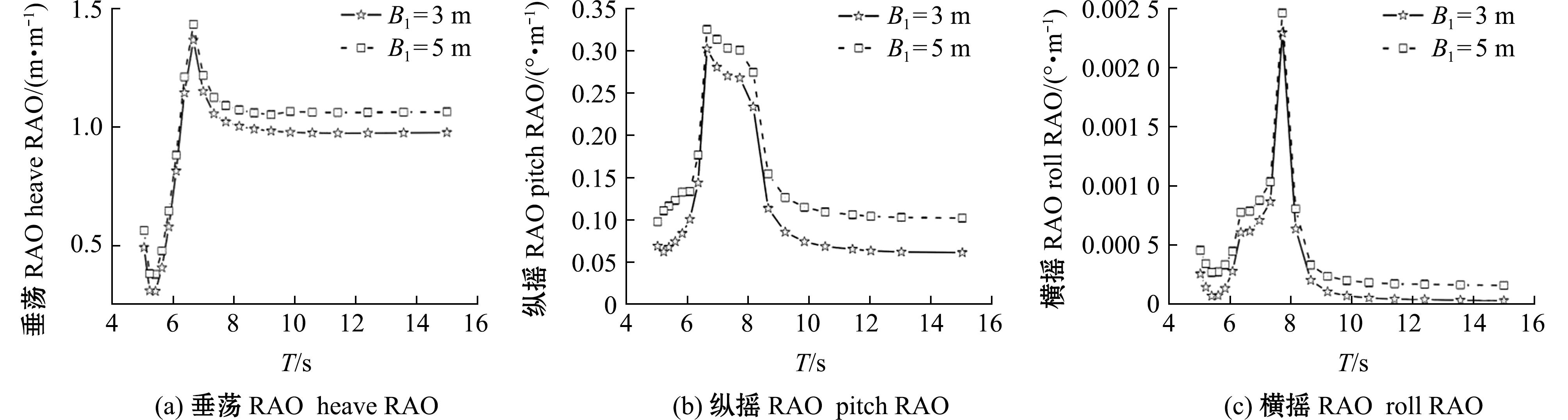
图9 不同OWC开孔宽度情况下的幅值响应算子
Fig.9 RAOs under different opening widths of OWC
3.5 吃水深度对稳定性的影响
为了研究结构吃水深度H1对浮堤系泊稳定性的影响,本研究中选取海水深度为25 m,双体间距为10 m,OWC开口宽度为3 m,对吃水深度不同的工况进行模拟,吃水深度可通过在双浮箱下部增加配重进行调整,可以得到垂荡、纵摇及横摇的运动幅值响应算子分别如图10所示。两条曲线分别对应吃水深度为5、6 m。从图10可见,两条曲线的变化趋势基本相同,随着周期的增加,运动幅值响应算子先增大后减小,在各自结构的固有周期时达到最大值。增大结构的吃水深度使垂荡、横摇方向的运动幅值响应算子略有增大,而纵摇方向的运动幅值响应算子明显减小,通过计算可得,当运动幅值响应算子取最大值时,垂荡方向的运动幅值响应算子增大了36.1%,横摇方向的运动幅值响应算子增大了13.2%,而纵摇方向的运动幅值响应算子减小了53.3%。另外,浮堤吃水深度的增大使结构的固有周期发生了较大改变,当结构的吃水深度为6 m时,固有周期为11.35 s。
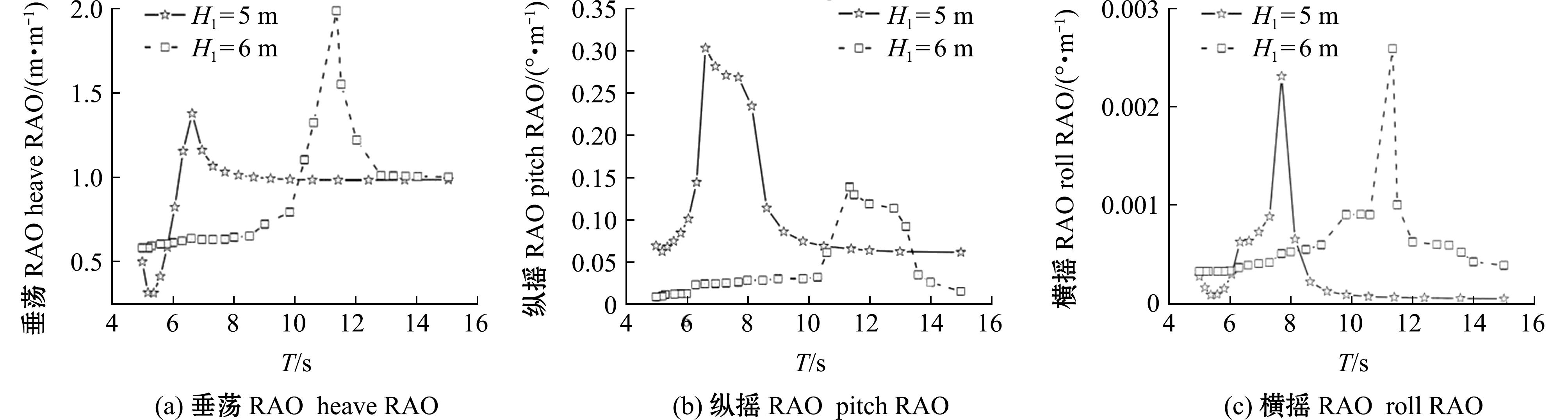
图10 不同吃水深度情况下的幅值响应算子
Fig.10 RAOs under different draft depths
3.6 锚链拖地长度对稳定性的影响
为了研究锚链拖地长度对OWC-开孔双体浮式防波堤系泊稳定性的影响,本研究中选取海水深度为25 m,双体间距为10 m,浮堤的OWC开口宽度为3 m,选取两种不同的锚链拖地长度分别为5、9 m,对其进行模拟,可以得到垂荡、纵摇及横摇的运动幅值响应算子分别如图11所示,两条曲线对应锚链拖地长度分别为9、5 m。从图11可见,当运动幅值响应算子取最大值时,随着锚链拖地长度的减小,垂荡及横摇方向的运动幅值响应算子有一定增大,而纵摇方向的运动幅值响应算子减小;从两种不同锚链拖地长度下运动幅值响应算子最大值的比较来看,与锚链拖地长度9 m相比,锚链拖地长度为5 m时垂荡方向的运动幅值响应算子增大了55.2%,横摇方向的运动幅值响应算子增大了39.1%,而纵摇方向的运动幅值响应算子减小了43.3%。
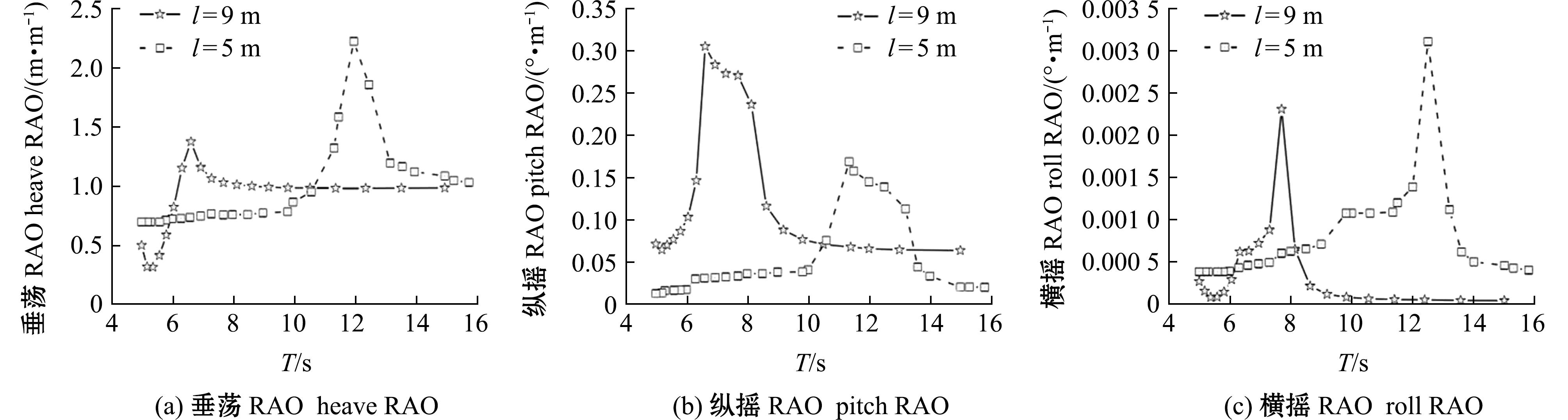
图11 不同锚链拖地长度情况下的幅值响应算子
Fig.11 RAOs under different anchor chain drag lengths
通过两条曲线的对比,可以看出锚链拖地长度为5 m时OWC-开孔双体浮式防波堤的固有周期明显大于锚链拖地长度为9 m时的固有周期,锚链拖地长度为5 m时垂荡方向的运动幅值响应算子取最大值时对应的固有周期为12 s,横摇方向的运动幅值响应算子取最大值时对应的周期为12.5 s,纵摇方向的运动幅值响应算子取最大值时对应的周期为11.35 s,即结构的固有周期为11.35~12.5 s,说明通过减小浮堤的锚链拖地长度可以增大结构的固有周期,使其更适合在波浪周期小于11.35 s的波况下应用。
4 结论
本研究中利用ANSYS AQWA对OWC-开孔式浮式防波堤进行数值模拟,讨论了浮堤组合双体结构的间距、开口宽度和锚泊方式等因素对浮堤系泊稳定性的影响规律,得到以下结论。
1)波浪入射角度的增大使浮堤系泊稳定性增加;OWC-开孔浮式防波堤双体间距的改变对稳定性无明显影响;OWC开口宽度增大将使浮堤的运动更为剧烈。
2)增大浮堤的吃水深度或减小锚链拖地长度使浮堤垂荡、横摇方向的运动增大,纵摇方向的运动减小;不论增大浮堤的吃水深度或减小锚链拖地长度都会使浮堤的固有周期增大,进而对系统的系泊稳定性产生影响。
[1] 栾英妮,陈汉宝.浮式防波堤研究进展[J].水运工程,2021(3):64-69.LUAN Y N,CHEN H B.Research progress of floating breakwater[J].Port &Waterway Engineering,2021(3):64-69.(in Chinese)
[2] WILLIAMS A N,LEE H S,HUANG Z.Floating pontoon breakwaters[J].Ocean Engineering,2000,27(3):221-240.
[3] KOFTIS T H,PRINOS P,KOUTANDOS E.2D-V hydrodynamics of wave-floating breakwater interaction[J].Journal of Hydraulic Research,2006,44(4):451-469.
[4] 郑艳娜,姚云鹏,董国海,等.波浪对双箱式浮式防波堤作用的时域数值模拟[C]//中国海洋工程学会.第十五届中国海洋(岸)工程学术讨论会论文集(中),太原:海洋出版社,2011:162-167.ZHENG Y N,YAO Y P,DONG G H,et al.The numerical simulation of double-boxes floating breakwater under wave conditions in time domain[C]//China Ocean Engineering Society.Proceedings of the 15th Marine (Coastal) Engineering Academic Symposium of China (Part 2),Taiyuan: China Ocean Press,2011:162-167.(in Chinese)
[5] 张天庚.多体组合式浮式防波堤水动力性能研究[D].大连:大连理工大学,2020.ZHANG T G. Research on hydrodynamic performance of multi-body composite floating breakwater[D].Dalian:Dalian University of Technology,2020.(in Chinese)
[6] 何梦程,单潜瑜,白兴兰,等.箱-板组合浮式防波堤水动力性能试验研究[J].浙江海洋学院学报(自然科学版),2019,38(3):237-243.HE M C,SHAN Q Y,BAI X L,et al.Experimental study of hydrodynamic analysis for the composite pontoon-plate floating breakwater[J].Journal of Zhejiang Ocean University (Natural Science Editon),2019,38(3):237-243.(in Chinese)
[7] 沈雨生,潘军宁,周益人,等.双浮箱式浮式防波堤消浪性能试验研究[J].海洋工程,2018,36(1):47-54.SEN Y S,PAN J N,ZHOU Y R,et al.Experimental study on wave attenuation performance of twin-pontoon floating breakwater[J]. The Ocean Engineering,2018,36(1):47-54. (in Chinese)
[8] SHUNICHI IKESUE,YASUHIRO SUGI.Study on the performance of a floating breakwater with two boxes[C].Japan,Paper presented at the The Twelfth International Offshore and Polar Engineering Conference,Kitakyushu,2002.
[9] 杨彪,陈智杰,王国玉,等.双浮箱-双水平板式浮式防波堤试验研究[J].水动力学研究与进展A辑,2014,29(1):40-49.YANG B,CHEN Z J,WANG G Y,et al.Experimental investigation of twin pontoon-twin horizontal plate floating breakwater[J].Chinese Journal of Hydrodynamics,2014,29(1):40-49.(in Chinese)
[10] 王环宇.多孔浮式防波堤的实验研究与数值模拟[D].大连:大连理工大学,2010.WANG H Y.Experimental study and numerical simulation of a porous floating breakwater[D].Dalian:Dalian University of Technology,2010.(in Chinese)
[11] 胡文清,余炜光,詹杰民,等.一种三维多孔结构的消波特性研究[C]//第十届全国流体力学学术会议论文摘要集,2018:185-186.HU W Q,YU W G,ZHAN J M,et al. Study on the wave attenuation characteristics of a three-dimensional porous structure[C]//Abstract Collection of Papers from the 10th National Conference on Fluid Mechanics,2018:185-186.(in Chinese)
[12] 刘心媚.多孔型浮式防波堤物理模型试验研究[D].大连:大连海洋大学,2019.LIU X M.Experimental study on physical model of porous floating breakwater[D].Dalian:Dalian Ocean University,2019.(in Chinese)
[13] 刘德兴,郑艳娜,张佳星.振荡水柱波能发电装置的研究应用进展[J].大连海洋大学学报,2015,30(2):231-236.LIU D X,ZHENG Y N,ZHANG J X.Research and application prospects of oscillating water column converter[J].Journal of Dalian Ocean University,2015,30(2):231-236.(in Chinese)
[14] HE F,HUANG Z H,WING-KEUNG LAW A.Hydrodynamic performance of a rectangular floating breakwater with and without pneumatic chambers:an experimental study[J].Ocean Engineering,2012,51:16-27.
[15] HE F,HUANG Z H.Hydrodynamic performance of pile-supported OWC-type structures as breakwaters:an experimental study[J].Ocean Engineering,2014,88:618-626.
[16] 于定勇,曲铭,谢雨嘉.一种集成OWC气室的桩基防波堤方案设计与试验研究[J].太阳能学报,2021,42(10):379-386.YU D Y,QU M,XIE Y J.Design and experimental study of a pile-based breakwater integrated OWC air chamber[J].Acta Energiae Solaris Sinica,2021,42(10):379-386.(in Chinese)
[17] TRIVEDI K,KOLEY S.Mathematical modeling of breakwater-integrated oscillating water column wave energy converter devices under irregular incident waves[J].Renewable Energy,2021,178:403-419.
[18] 李佳繁,郑艳娜,林裕强,等.OWC-开孔浮式防波堤消浪性能的数值研究[J].水运工程,2022(6):21-28.LI J F,ZHENG Y N,LIN Y Q,et al.Numerical study on wave dissipation performance of OWC perforated floating breakwater[J]. Port &Waterway Engineering,2022(6):21-28. (in Chinese)
[19] 张翔宇,宁德志,MAYON ROBERT,等.透空防波堤和振荡水柱波能装置集成系统水动力性能研究[J/OL].工程力学:1-8[2024-01-10].http://kns.cnki.net/kcms/detail/11.2595.03.20230327.1126.012.html.ZHANG X Y,NING D Z,Robert M,et al.Research on hydrodynamic performance of integrated system of permeable breakwater and oscillatine water column wave energy device [J/OL].Engineering Mechanics:1-8[2024-01-10].http://kns.cnki.net/kcms/detail/11.2595.03.20230327.1126.012.html.
[20] CHENG Y,FU L,DAI S S,et al.Experimental and numerical analysis of a hybrid WEC-breakwater system combining an oscillating water column and an oscillating buoy[J].Renewable and Sustainable Energy Reviews,2022,169:112909.
[21] CHENG Y,DU W M,DAI S S,et al.Hydrodynamic characteristics of a hybrid oscillating water column-oscillating buoy wave energy converter integrated into a π-type floating breakwater[J].Renewable and Sustainable Energy Reviews,2022,161:112299.
[22] 马永洁.三维浮式防波堤消波性能研究[D].哈尔滨:哈尔滨工程大学,2017.MA Y J.Wave dissipation study of 3D floating breakwater[D].Harbin:Harbin Engineering University,2017.(in Chinese)
[23] 王铁涛,刘祚秋.双浮箱-双水平板浮式防波堤的数值模拟[J].水运工程,2016(3):46-50.WANG T T,LIU Z Q.Numerical simulation of twin pontoon-twin horizontal plate floating breakwater[J].Port &Waterway Engineering,2016(3):46-50.(in Chinese)