近年来,随着船舶数量的不断增长,船舶的航行路径也变得越来越复杂。在复杂的海洋环境中,设计出有效的船舶路径规划方法显得十分重要,一方面有利于促进船舶智能化水平的发展,另一方面可以降低碰撞事故发生率,使船舶航行更加安全。其中,船舶路径规划中所使用的算法是提高路径规划效率和安全性的一种重要手段[1]。
目前,传统船舶路径规划算法主要包括A*算法、人工势场法(artificial potential field,APF)[2]、蚁群算法[3]和遗传算法[4]等;近几年也出现了一些新型的路径规划算法,如深度强化学习算法[5]、D*算法[6],以及其他一些基于传统路径规划算法进行融合和改进的算法。1968年,由斯坦福研究院(Stanford Research Institute)Hart等[7]提出的A*算法是一种较常用的路径查找和图形遍历算法,其具有较好的可拓展性、启发性和准确性,被认为是Dijkstra算法的扩展,被广泛应用于解决路径规划的方法中。针对A*算法当前存在的部分缺陷,采用平滑冗余节点、改进评价函数、曲线优化轨迹和改进启发函数等方式可在一定程度上提高路径规划算法效率,但规划出的路径并不能满足路径最短的条件[8-11]。圆弧距离法和改进A*算法并融合角度信息可以在上述方法的基础上缩短规划路径长度,同时也出现了冗余拐点过多的情况[12-13]。在双向A*算法的基础上进行改进同样能够提高算法搜索效率和缩短规划路径长度,如多层双向A*算法[14]、双向时效A*算法等[15]。人工势场法作为当前主流的路径规划算法,在改进后可达到解决其局部最小值问题的效果[16]。将协作避障算法[17]、加入全局路径引力[18]和进行航线规划引导[19]等方法用于人工势场法均实现了较为不错的改进效果。但融合算法同时解决全局非最优解和局部最优解等问题的效果并不佳。
目前,常规的船舶路径规划算法在静态环境中存在搜索时间长、规划路径冗余拐点多等问题,而在动态环境中无法达到避障要求,采用双向A*算法虽然可缩短全局路径搜索时间,但仍无法完全解决上述问题。本研究中,提出双向A*-APF算法,在栅格化地图的基础上对双向A*算法在原有路径上进行优化,根据原始路径与障碍物的坐标点输出优化路径的直线距离代价,选取最小值进行优化,从而得到更短路径,提高路径规划的效益性;同时考虑环境中的动态障碍物,融合人工势场法对路径上的动态障碍物进行避障,保障了路径规划的安全性;最后利用MATLAB在静态环境中与传统A*算法和双向A*算法进行对比,验证本研究中方法的有效性,并在动态环境中模拟船舶避碰仿真试验来验证本研究中融合算法的可行性,以期为改进船舶路径规划研究提供参考。
1 全局路径规划算法
1.1 环境建模
船舶在进行路径规划前,需要提前获取静态环境的信息。静态信息是指船舶所处环境中障碍物的具体位置、大小,以及其是否会对船舶正常航行产生不良影响。环境建模是将环境中的特征、障碍物及其他相关信息转化为计算机可处理的形式,以支持船舶或自动系统在复杂环境中进行路径规划。目前的路径规划环境建模涉及多种方法和技术,常见的环境建模方法有栅格法、拓扑法、点云法和单元树法等。由于栅格法具有简单直观、可扩展性、可解释性及天然适用于障碍物避障等优点,本研究中采用该方法进行环境建模。图1为栅格化地图的环境建模,其中,黑色方块表示障碍物所在位置及大小,白色方块为船舶可航行区域。
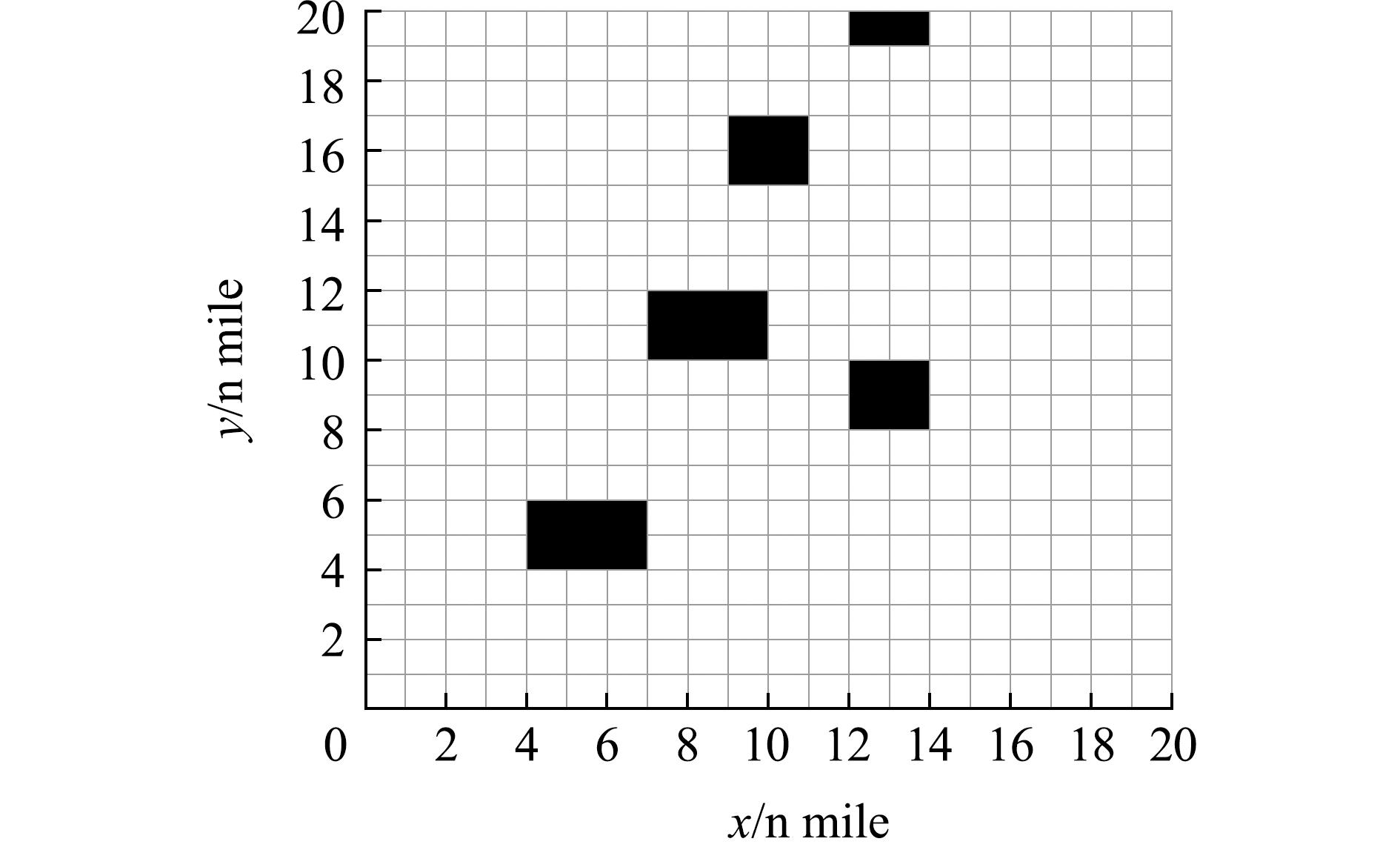
图1 栅格化地图
Fig.1 Grid-based map
1.2 传统A*算法
A*算法是一种经典的启发式搜索算法,用于在图或网格中找到两个节点之间的最短路径。它在路径搜索中结合了最佳优先搜索和Dijkstra算法的思想,具有高效性和可行性。其基本步骤如下:
1)初始化。将起点加入开放集(OpenList),设置起点的代价为0,计算起点到目标点的启发式估计值(H值)。
2)主循环。如果开放集非空,则选择开放集中具有最小总代价(F值)的节点作为当前节点,将该节点从开放集移入封闭集;如果当前节点是目标节点,算法结束,路径找到。对当前节点的相邻节点进行遍历,如果相邻节点不可通行或已在封闭集中,则忽略它;如果相邻节点不在开放集中,将其添加到开放集,同时计算并更新它的代价和启发式估计值;如果相邻节点已在开放集中,则检查通过当前节点到达相邻节点的路径是否更优,如果是,则更新相邻节点的代价和路径信息。
3)路径重构。如果目标节点被找到,从目标节点开始,沿着父节点指针一直追溯到起点,构建路径。
评价函数f(n)是A*算法的关键,其综合考虑了两个因素:从起始节点到当前节点的实际代价g(n)和从当前节点到目标节点的估计代价h(n)。f(n)评价函数可以表示为
f(n)=g(n)+h(n)。
(1)
1.3 双向A*算法
双向A*算法是A*算法的一种变体,旨在提高搜索效率。传统的A*算法是从起始节点开始,逐步向目标节点搜索,扩展开放集中的节点。而双向A*算法则是从起始节点和目标节点同时开始搜索,分别维护两个开放集,然后尝试在两个方向上逼近彼此,直到它们在中间某个节点相遇。基础的双向A*算法要经历初始化、交替搜索、扩展节点、终止和路径回溯等步骤。双向A*算法的评价函数表示为
ff(n)=gf(n)+hf(n),
(2)
fb(n)=gb(n)+hb(n)。
(3)
式中:ff(n)为从起始节点到节点n的估计总代价;fb(n)为从节点n到目标节点的估计总代价;gf(n)为从起始节点到节点n的实际代价;gb(n)为从目标节点到节点n的实际代价;hf(n)为从节点n到目标节点的启发式估计代价;hb(n)为从节点n到起始节点的启发式估计代价。
为了还原现实中的海图,本研究中将黑色障碍物替换为黄色障碍物,基础双向A*算法如图2所示。双向A*算法的关键在于同时从两个方向进行搜索,这大大减少了搜索的空间。相比传统的A*算法,双向A*算法在某些情况下可以显著提高搜索效率,特别是在路径搜索空间较大的情况下。因此,本研究中采用双向A*算法作为全局路径规划算法,以解决传统A*算法在进行路径规划时出现的搜索时间较长、效率较低的问题。
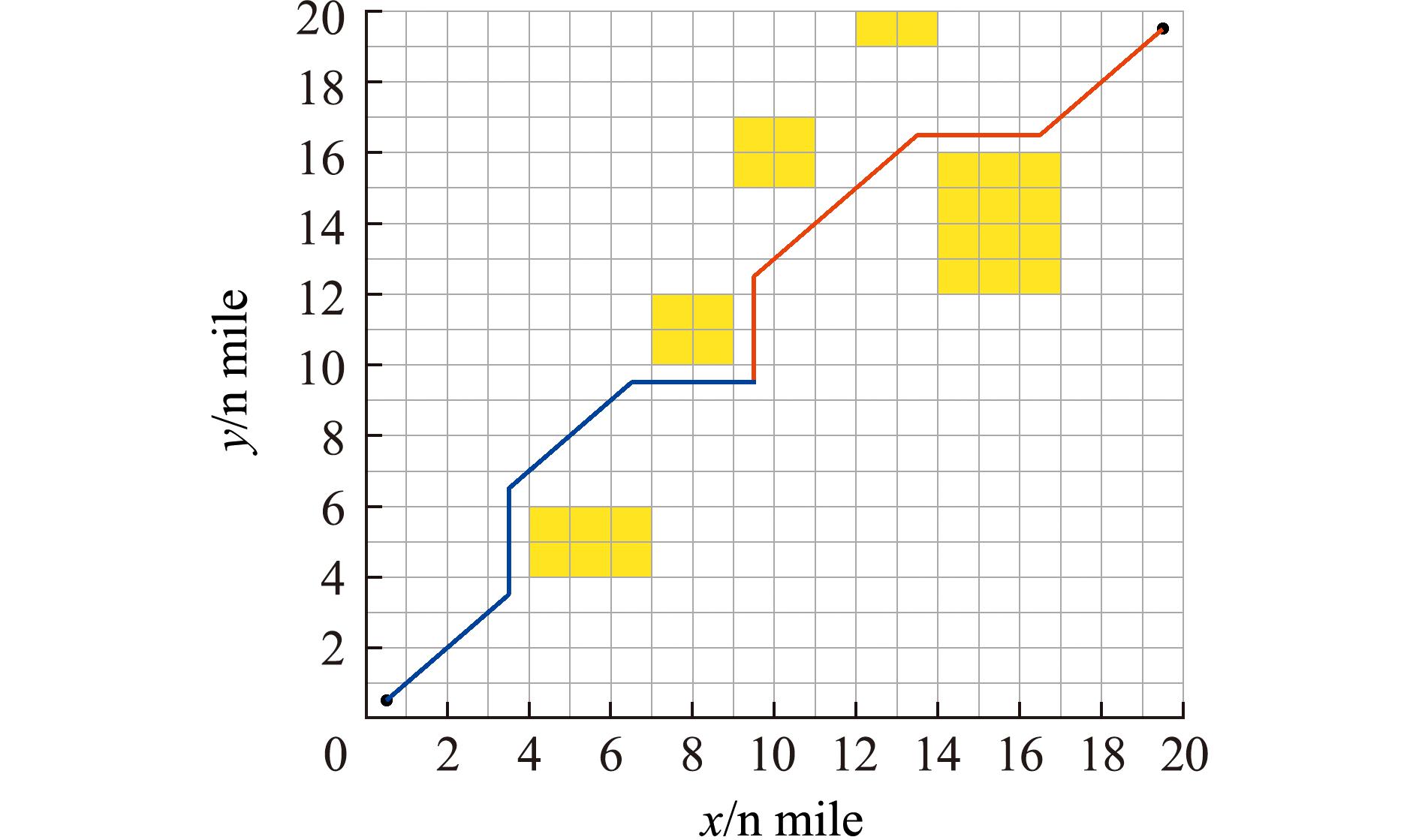
图2 基于基础双向A*算法的路径规划示意图
Fig.2 Schematic diagram of path planning based on bidirectional A* algorithm
1.4 改进双向A*算法
从图2可见,双向A*算法仍存在路径拐点较多,以及在无障碍物区域选择的路径并非最短的现象。因此,本研究中在双向A*算法的基础上进行改进,加入M矩阵,M矩阵是一个用于表示移动的8×2矩阵,其中,每一行表示一种可能的移动方向,每个元素表示一个二维坐标中的移动步骤。这些元素可以在栅格图上判断移动方向、寻找路径,最终检查邻居节点的可行性并将其记录,如是否超出了地图边界,是否是障碍物等。在代码的循环中,M矩阵的每一行被用于计算节点的邻居节点坐标,记录不可移动的障碍物坐标点sign值,用于判断节点是否可以作为朝向目标点进行移动的路径点,以及能否在此节点上生成规划路径。加入PathOptimization函数对路径进行优化,将原始路径的坐标矩阵、需要优化路径的坐标点、地图的障碍物分布及地图的行数与列数作为输入参数,将优化后路径的直接距离和坐标作为输出参数。为保证起点和终点不会被去除,在循环遍历路径时会以第二索引点为起始点,倒数第二索引点为终点,在遍历路径时加入IsClear函数用于判断两个点之间是否设有障碍物,即路径上的点是否为非冗余点。该函数接收需要判定的冗余两拐点的坐标及地图上障碍物的坐标3个输入参数,根据输入冗余两拐点的坐标划分出矩形区域并遍历其中的单元格,若其中不包含障碍物则认为可以进行路径优化。完成此种路径优化可以达到去除冗余拐点、缩短路径距离和减少不必要转向的效果。改进双向A*算法的流程见图3,改进双向A*算法见图4。基础双向A*算法与改进双向A*算法的路径规划数据对比见表1。
表1 基础双向A*算法与改进双向A*算法的路径规划数据对比
Tab.1 Comparative analysis of path planning data between bidirectional A* algorithm and enhanced bidirectional A* algorithm

路径规划算法path planning algorithm规划路径长度/n milepath length planning拐点数量number of turning point双A∗算法bidirectional A∗ algorithm30.387改进双向A∗算法enhanced bidirectional A∗ algorithm28.193

图3 改进双向A*算法流程图
Fig.3 Flowchart of enhanced bidirectional A* algorithm

图4 基于改进双向A*算法的路径规划示意图
Fig.4 Schematic diagram of path planning based on enhanced bidirectional A* algorithm
2 局部路径规划及融合算法
2.1 改进人工势场法
人工势场法是一种在路径规划、自主导航和避障中常用的方法,其通过在环境中引入虚拟势能场,使船舶受到来自目标的引力和来自障碍物的斥力,从而在环境中移动并避开障碍物,达到预定目标。该方法的基本思想类似于物理学中势能和力的概念。
引力计算方法为
Fa=-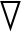 Ua(X)=-ka|X-Xg|,
Ua(X)=-ka|X-Xg|,
(4)
(5)
式中:Fa为引力;ka为引力增益系数;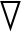 Ua(X)为引力的梯度;Xg为目标点的位置向量;X为本船的位置向量。
Ua(X)为引力的梯度;Xg为目标点的位置向量;X为本船的位置向量。
斥力计算方法为
Fr=-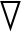 Ur(X),
Ur(X),
(6)
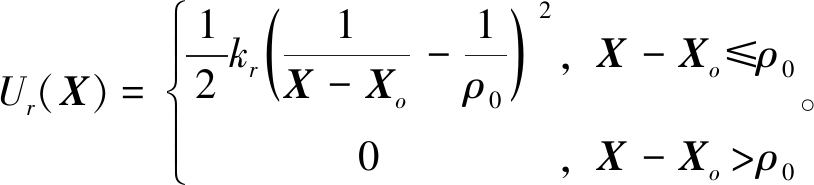
(7)
式中:Fr为斥力;kr为斥力增益系数;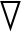 Ur(X)为斥力的梯度;Xo为障碍物的位置向量;ρ0为船舶能够受到障碍物斥力的范围。
Ur(X)为斥力的梯度;Xo为障碍物的位置向量;ρ0为船舶能够受到障碍物斥力的范围。
合力方向计算公式为
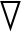 U=
U=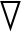 Ua+
Ua+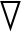 Ur,
Ur,
(8)
F=Fa+Fr。
(9)
式中: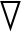 U为合力的梯度;F为合力。
U为合力的梯度;F为合力。
人工势场法的优点包括简单易懂、适用于复杂环境及具有实时性等,然而其也存在一些不足,如局部最优解问题、震荡问题等。因此,本研究中在传统人工势场法的基础上加以改进,在原斥力场函数的基础上引入船舶与临时终点之间的距离X-Xg,更改出新的斥力场函数和相应的斥力函数,即
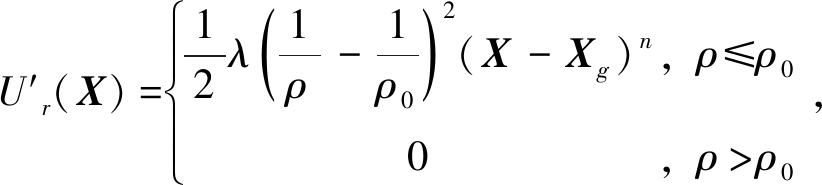
(10)
(11)
(12)
(13)
式中:ρ为船舶当前位置与障碍物之间的距离;λ为斥力系数;n为任意大于0的实数;Fr1和Fr2为斥力分量;Fr1方向为障碍物到船舶;Fr2方向为船舶到障碍物。
将改进后的人工势场法应用于离散化后的路径上,加入step_length函数来表示路径离散化的步长,离散化是将路径上相邻两点之间按照设定的步长均匀插入,以便在每一步中进行路径规划和移动;传统人工势场法中,引力方向是直接指向目标点的,而本研究中将斥力方向根据船舶所在位置与静态动态障碍物之间的距离进行调整,即设定阈值,以避免进入震荡或陷阱区域;传统人工势场法通常只有一个最终目标点,而本研究中为船舶在特定的步数后设定一个临时终点,用next_step_num表示其坐标,这个临时终点会在每次到达后更新,以确保船舶朝着终点前进。
2.2 双向A*-APF算法
改进后的双向A*算法可以用于全局路径规划,但缺乏对路径上出现的动态障碍物避障的能力,而融合了改进后人工势场法的算法(A*-APF)可以有效地解决这个缺陷,达到更好的路径规划效果。
双向A*-APF算法的流程如图5所示。首先,在静态环境中利用改进后的双向A*算法进行寻路,得到一条完整的路径,再将此路径离散化,用于动态避障。在船舶沿着规划好的路径前进时,采用改进后的人工势场法检测与判断在动态环境下依照此路径行进是否存在障碍物对本船构成碰撞危险,并能在存在碰撞危险的情况下采取避碰行动。人工势场法将对目标点的引力与来自障碍物的斥力相结合,以引导船舶沿着安全路径移动。在计算斥力时考虑动态障碍物,同时检查船舶是否在动态障碍物的感应距离内,并相应地调整斥力。在完成动态障碍物避障后,以全局规划路径作为目标点,引导船舶回归至最初规划好的路径上,不断循环,直至到达路径规划终点。
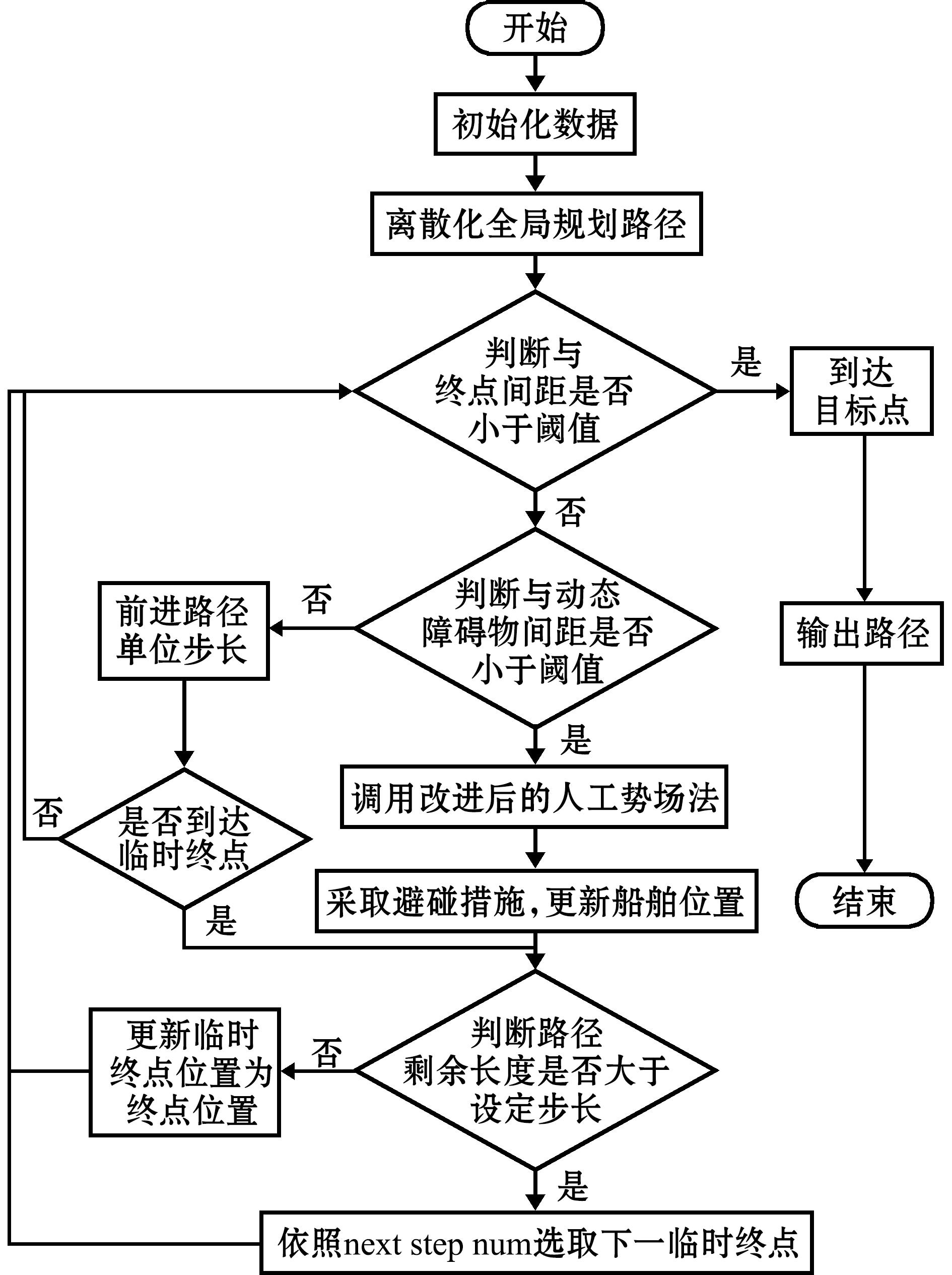
图5 双向A*-APF算法流程
Fig.5 Flowchart of bidirectional A*-APF algorithm
3 仿真验证
3.1 全局路径规划算法验证
在MATLAB R2020b中进行对比试验,通过在相同障碍环境下,对比传统A*算法、双向A*算法和改进双向A*算法规划路径的各项数据,验证改进双向A*算法的优越性。本次试验仿真栅格图大小为20×20,单位栅格边长为1 n mile,逐渐增加障碍物数量,路径规划起始点为左下角,目标点为右上角。
仿真结果如图6、图7所示,各个算法在不同复杂度栅格图中的路径规划数据如表2所示。根据试验结果可知,传统A*算法在不同复杂的栅格图中都存在规划路径长度偏长、搜索时间偏长和拐点偏多的问题。双向A*算法虽然能够有效地缩短算法搜索时间,但是并没有改善拐点较多、路径长度较长的问题。而改进的双向A*算法在保证了高效搜索时间的基础上,能够有效地减少路径拐点、缩短路径长度。对比传统A*算法,改进双向A*算法的路径长度缩短了4%~10%,拐点减少了44%~50%,搜索时间减少了85%~90%;对比双向A*算法,改进双向A*算法的路径长度缩短了6%~8%,拐点减少了50%~62%,搜索时间减少了8%~10%。通过分析可知,本研究中所采用的改进双向A*算法的全局路径规划算法在简单和复杂的环境下都能够很好地适应,该规划算法较为稳定地缩短了路径长度;提高了搜索效率,缩短了搜索时间;减少了路径上的冗余拐点。因此,本研究中提出的全局路径规划算法具有一定的优越性。
表2 各个算法在不同复杂度栅格图中的路径规划数据
Tab.2 Path planning data for various algorithms in grid maps with different complexities

栅格图序号grid map index路径规划算法path planning algorithm障碍物栅格数量obstacle grid路径长度/n milepath length拐点数量number of turning point搜索时间/ssearch time传统A∗32.1490.191双向A∗4031.21130.03改进双向A∗28.8550.03传统A∗33.90160.322双向A∗12034.73160.03改进双向A∗32.5280.03
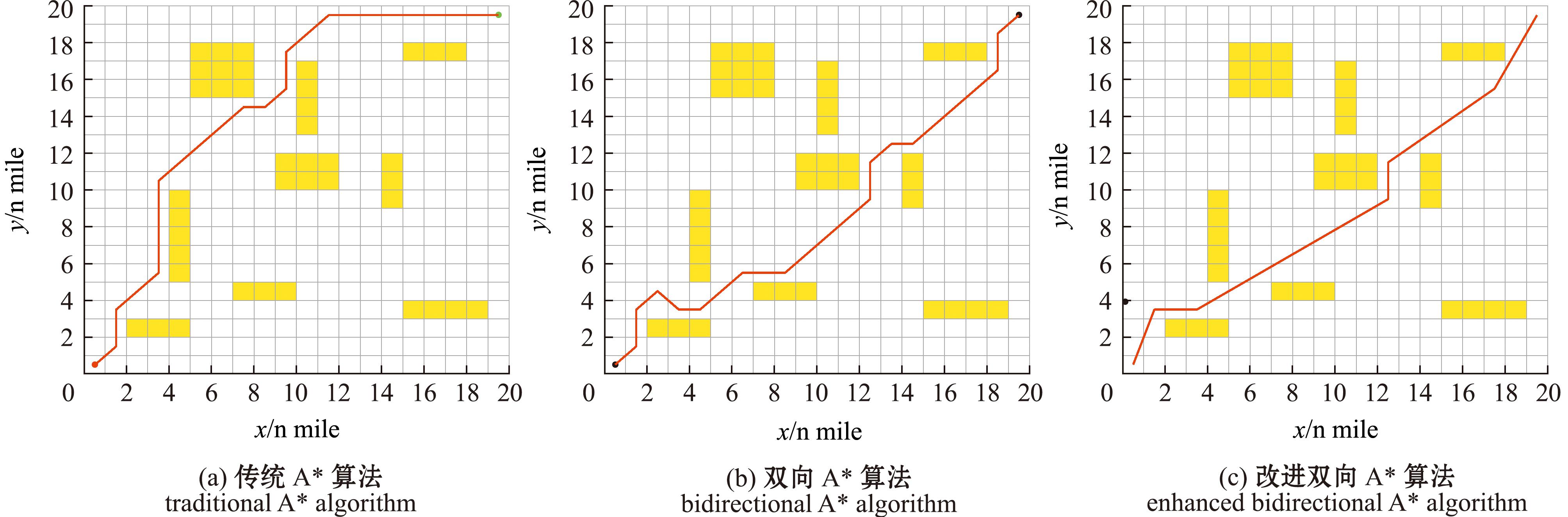
图6 栅格图1仿真结果
Fig.6 Simulation results for grid map 1
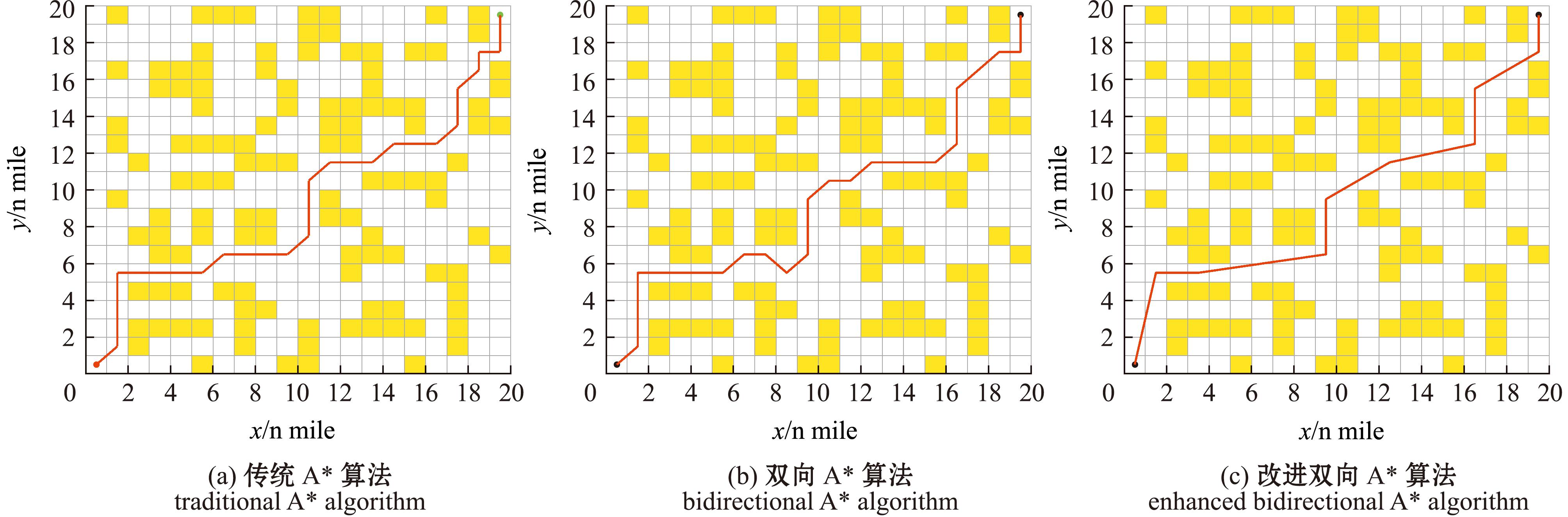
图7 栅格图2仿真结果
Fig.7 Simulation results for grid map 2
在完成随机障碍物栅格静态避障后,本研究中以大连市南部海域进行模拟作为仿真试验栅格图的基础,将其中陆地、海岛、浅水水域及附近沉船点视为静态障碍物并进行栅格化,栅格图大小为50×50,单位栅格边长为1.4 n mile。
仿真结果如图8所示,传统A*算法和本研究中的改进算法在海图模拟仿真试验中的路径规划数据如表3所示。根据试验结果可知,改进算法相较于其他算法能够为船舶路径规划缩短了一定路径长度,在减少了不必要拐点的情况下,规划出来的路径更符合日常的船舶操纵习惯,且极大地提高了路径规划搜索效率。
表3 3种算法在海图模拟仿真试验中的路径规划数据
Tab.3 Path planning data in simulated navigation experiments with nautical charts for three algorithms

路径规划算法path planning algorithm 路径长度/n milepath length拐点数量number of turning point搜索时间/ssearch time传统A∗ traditional A∗ 119.98120.73双向A∗ bidirectional A∗ 119.98150.07改进双向A∗enhanced bidirectional A∗ 113.4050.06
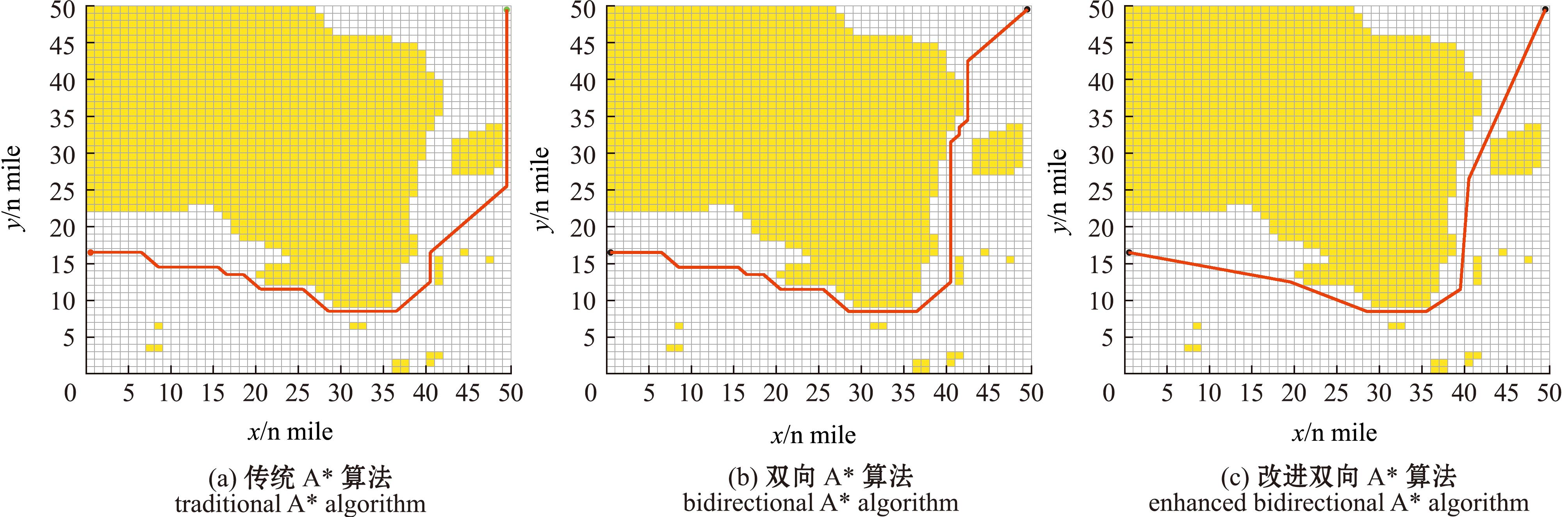
图8 海图模拟仿真结果
Fig.8 Simulation results on nautical charts
3.2 双向A*-APF算法验证
本研究在MATLAB R2020b中进行双向A*-APF算法试验,通过在上文中栅格图2(图7)的环境下进行模拟,静态障碍物数量和位置不变,在其中增加4个动态障碍物,位置放置在已规划好的路径附近,以验证本研究算法的有效性和安全性。本次试验仿真地图大小为20×20,单位栅格边长为1 n mile,静态障碍物数量为120个,动态障碍物数量为4个,颜色为灰色,由左至右分别以坐标(1,6)、(8,10)、(11,4)、(16,16)为起点做向上、向右、向右、向左前进距离为1 n mile的周期往复运动,路径规划起始点为左下角,目标点为右上角,红线为全局算法规划出的路径,绿线为船舶考虑动态障碍物后的实时路径。
从图9可见:在船舶即将遇到动态障碍物时,通过双向A*-APF算法可检测动态障碍物是否在本船全局路径规划航线上;当动态障碍物对船舶构成碰撞危险时,会提前进行避障行动,同时在规避动态障碍物时,依然能够保持和静态障碍物之间的安全距离;在完成避障行动后,船舶能够回到全局路径规划算法部分所规划的路线上,最终安全到达目标点,验证了局部路径规划的有效性和安全性。
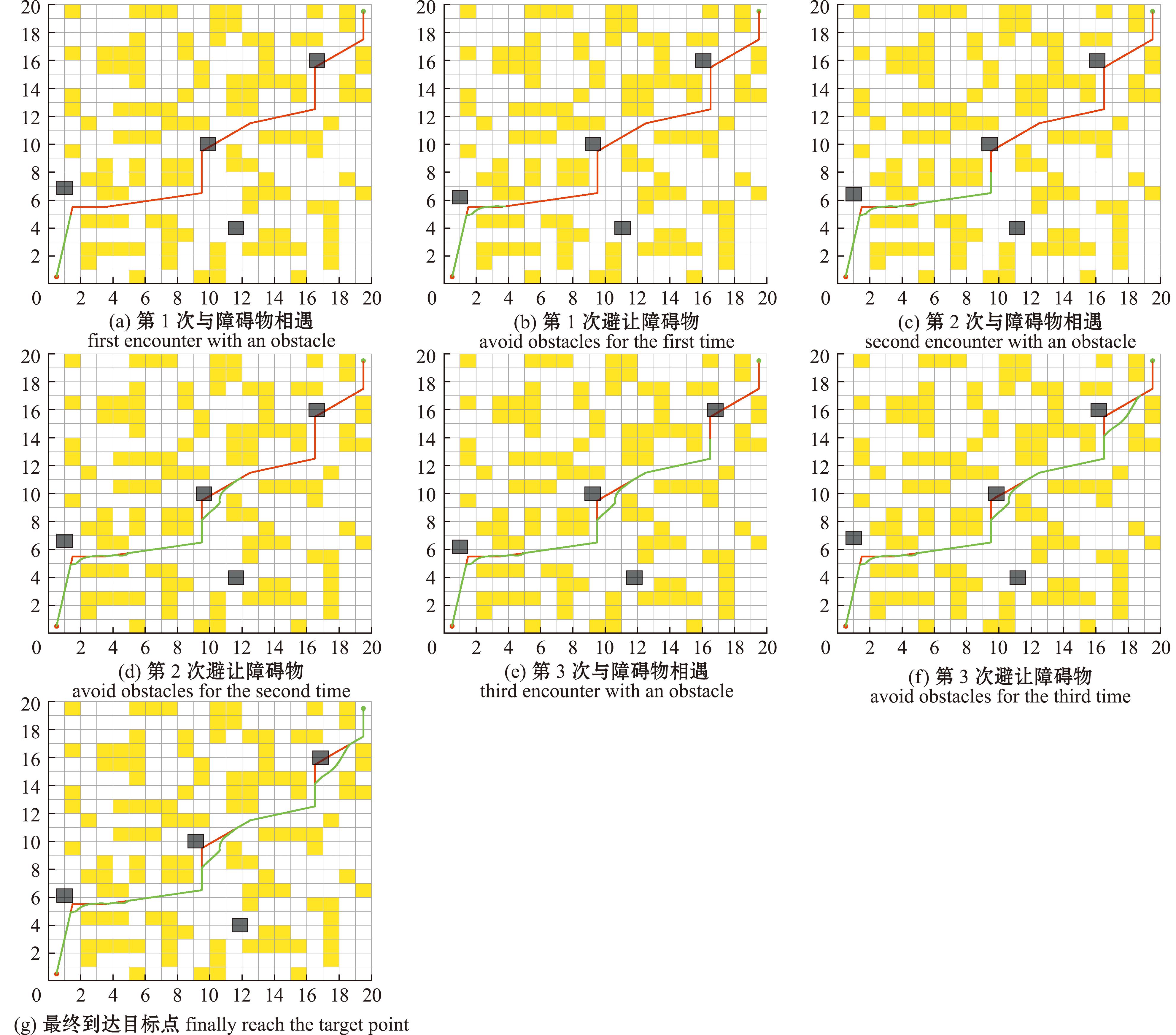
图9 双向A*-APF算法栅格图仿真结果
Fig.9 The grid map simulation results by bidirectional A*-APF algorithm
经过上述仿真试验可看出,船舶在第1次避让动态障碍物时,为了完成避碰行动,同时保障船舶与静态障碍物之间的安全距离,出现了接近直角的转向角度,这在一定程度上并不符合日常船舶的操纵习惯。鉴于上述模拟试验是基于理论上的栅格图进行的,现实船舶航行几乎不会出现如此复杂的航行局面,故本研究中在图8海图的基础上加入动态障碍物来模拟船舶在实际海洋情况中的算法试验。
从图10可见,在本次仿真试验中,船舶先后与动态障碍物经历了多种会遇局势,包括4次不同角度的交叉相遇局面及1次追越局面,均能够完成避碰,且所采取的行进路径也能满足当下船舶操纵性能的需求。从图10(h)还可见,本船在进行追越时,虽然两侧均存在岛屿,进行追越行为的环境条件较为恶劣,但在完成追越行为后船舶仍旧能够保持与岛屿之间的安全距离,最终安全到达模拟试验的终点。原规划路径长度为113.40 n mile,本次试验中,船舶面对动态障碍物完成避碰行动的情况下行进路径长度为114.05 n mile,由此可见,船舶在保证采取有效避碰行为的基础上并未进行过长的绕行,有效验证了本研究中所提出的双向A*-APF算法在实际船舶路径规划中的可行性。

图10 双向A*-APF算法海图仿真结果
Fig.10 The marine chart simulation results by bidirectional A*-APF algorithm
4 讨论
4.1 全局路径规划算法的改进
A*算法作为一种经典的启发式搜索算法,其可改进的空间一直在被发掘。以A*算法为基础引入跳点概念进行跳点搜索,可以缩短算法运行时间,提高路径规划效率[20]。双向A*算法可以进一步降低路径搜索需要的时间,很大程度上提高了算法的实时性;该算法通过关键点选择策略,剔除了路径的冗余节点,缩短了路径的长度[21]。基于双向A*算法的高效路径规划算法可生成更有效的规划路径[22]。目前,改进方法已实现了对A*算法路径规划成效的提高[8-15],但改进算法仍然存在全局路径并非最优的问题,因此,实现兼具减少拐点、缩短规划路径长度和找出全局最优路径的路径规划算法具有重要意义。本研究中通过引入优化函数PathOptimization和IsClear改进了双向A*算法输出优化后路径的坐标矩阵,并生成了全局最优路径,通过与传统A*算法和双向A*算法在虚拟栅格图和海图中进行模拟试验对比,结果表明,平均减少了50%左右的冗余拐点,平均减少了47.5%的算法搜索时间,规划路径长度平均缩短了7%左右,说明全局路径规划算法的改进具有一定有效性。
4.2 局部条件的算法融合
人工势场法是局部路径规划中比较常用的算法,该算法对静态障碍物和动态障碍物均可实现避碰效果。已有研究证明,相关算法存在多种方法解决局部最优解问题[16-19]。本研究中采用了设定斥力阈值和临时终点的方式对人工势场法进行改进,并加入了离散化初始路线的步骤为实现算法融合做准备。目前,应用于路径规划的融合算法研究较多,将优化后A*算法与人工势场法融合,可在静态障碍物的条件下快速完成全局路径规划,同时避免了局部最优的困境[23];而APF-IRRT*混合算法进一步缩短了路径长度和搜索时间[24]。但上述融合算法并不能同时解决目前路径规划算法存在的全局非最优解和局部最优解等问题,故本研究中提出双向A*-APF算法,并进行了模拟试验。本研究结果表明,融合算法在较为复杂的试验环境中能够有效规避动态障碍物,实现了在完成避碰行动后返回原计划航线上的预期;本算法在海图模拟试验中面对多种角度的对遇局面和追越局面均能采取有效避碰措施,绕行长度约为0.65 n mile,验证了本研究中算法在实际船舶路径规划中的可行性。
在局部路径算法领域中,现已实现了符合国际海上避碰规则的改进人工势场法,以更加贴合实际的方式解决了无人水面艇的动态避撞问题[25]。故本研究中算法在进行避碰行动时所采取的船舶操纵方式仍然需要进行进一步探究。
5 结论
1)本研究中提出的双向A*-APF算法,在保证搜索时长的同时,剔除路径上冗余拐点,缩短了规划路径的长度,与传统A*算法和双向A*算法相比,各项数据均有进步,得到了较为理想的试验结果,解决了传统A*算法规划路径并非最短、路径上拐点较多和搜索时间长等问题。
2)本研究中在全局路径规划的基础上,对局部动态障碍物利用改进后的人工势场法进行避障,试验证明在复杂的静态环境下,双向A*-APF算法依然能够识别出动态障碍物的位置,在保障安全性的同时能规避静态障碍物和动态障碍物,到达目标点,完成路径规划,同时解决目前路径规划算法存在的全局非最优解和局部最优解等问题。
[1] 程细得,刘鹏辉,韩琨羽,等.基于人工势场-操纵运动混合模型的船舶路径规划[J].华中科技大学学报(自然科学版),2023,52(1):85-90.CHENG X D,LIU P H,HAN K Y,et al.Path planning of ship based on artificial potential field-maneuvering motion hybrid model[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2023,52(1):85-90.(in Chinese)
[2] 张鹏,葛中盛,徐效农,等.一种基于人工势场法的自动驾驶汽车主动避障路径规划算法[J].智能计算机与应用,2020,10(9):174-177.ZHANG P,GE Z S,XU X N,et al.An active obstacle avoidance path planning algorithm for automatic driving vehicle based on artificial potential field method[J].Intelligent Computer and Applications,2020,10(9):174-177.(in Chinese)
[3] 李奇才,舒远仲,洪宇轩.一种蚁群算法与自适应机制的路径规划算法优化[J].机械科学与技术,2022,41(7):1095-1101.LI Q C,SHU Y Z,HONG Y X.Optimizing path planning algorithm based on ant colony algorithm and adaptive mechanism[J].Mechanical Science and Technology for Aerospace Engineering,2022,41(7):1095-1101.(in Chinese)
[4] 韩菊.基于遗传算法的机器人自定位、路径规划研究[J].电脑与电信,2022(12):77-81.HAN J.Research on robot self-localization and path planning based on genetic algorithm[J].Computer &Telecommunication,2022(12):77-81.(in Chinese)
[5] 宋大雷,吕昆岭,陈小平,等.基于深度强化学习的无人船全覆盖路径规划[J].现代电子技术,2022,45(22):1-7.SONG D L,LÜ K L,CHEN X P,et al.USV coverage path planning based on deep reinforcement learning[J].Modern Electronics Technique,2022,45(22):1-7.(in Chinese)
[6] 程满,杨光永,徐天奇,等.基于电子地图的D*补偿算法AGV路径规划[J].计算机与数字工程,2022,50(10):2187-2191.CHENG M,YANG G Y,XU T Q,et al.Compensation for D* algorithm for AGV path planning based on electronic map[J].Computer &Digital Engineering,2022,50(10):2187-2191.(in Chinese)
[7] HART P E,NILSSON N J,RAPHAEL B.A formal basis for the heuristic determination of minimum cost paths[J].IEEE Transactions on Systems Science and Cybernetics,1968,4(2):100-107.
[8] 沈克宇,游志宇,刘永鑫,等.基于改进A*算法的移动机器人路径规划[J].计算机应用研究,2023,40(1):75-79.SHEN K Y,YOU Z Y,LIU Y X,et al.Mobile robot path planning based on improved A*algorithm[J].Application Research of Computers,2023,40(1):75-79.(in Chinese)
[9] 赵春宇,姜皓,徐茂竹,等.改进A*算法在无人船路径规划中的应用[J].浙江工业大学学报,2022,50(6):615-620.ZHAO C Y,JIANG H,XU M Z,et al.Application of improved A*algorithm in unmanned ship path planning[J].Journal of Zhejiang University of Technology,2022,50(6):615-620.(in Chinese)
[10] KARLIJN F,JOOST V E.Efficient path planning for automated guided vehicles using A* algorithm incorporating turning costs in search heuristic[J].International Journal of Production Research,2023,61(3):707-725.
[11] LI H,CHU Z Y,FANG Y,et al.Source-seeking multi-robot team simulator as container of nature-inspired metaheuristic algorithms and astar algorithm[J].Expert Systems with Applications,2023,233:120932.
[12] 朱文亮,黄天意.基于改进A*算法的无人船全局路径规划的研究[J].科学技术创新,2023(1):213-216.ZHU W L,HUANG T Y.Research on global path planning of unmanned ships based on improved A* algorithm[J].Scientific and Technological Innovation,2023(1):213-216.(in Chinese)
[13] 张浩,庞宁林,胡安康,等.基于改进A*算法融合角度信息的船舶路径规划[J].上海海事大学学报,2023,44(2):6-10.ZHANG H,PANG N L,HU A K,et al.Ship path planning based on improved A* algorithm and adding angle information[J].Journal of Shanghai Maritime University,2023,44(2):6-10.(in Chinese)
[14] 杜婉茹,王潇茵,贾福凯,等.基于多层双向A*的未知环境路径规划算法研究[J].计算机应用与软件,2019,36(12):261-267.DU W R,WANG X Y,JIA F K,et al.Path planning in unknown environment based on multi-layer bi-A* algorithm[J].Computer Applications and Software,2019,36(12):261-267.(in Chinese)
[15] 高民东,张雅妮,朱凌云.应用于机器人路径规划的双向时效A*算法[J].计算机应用研究,2019,36(3):792-795,800.GAO M D,ZHANG Y N,ZHU L Y.Bidirectional time-efficient A* algorithm for robot path planning[J].Application Research of Computers,2019,36(3):792-795,800.(in Chinese)
[16] HAO G Q,LV Q,HUANG Z,et al.UAV path planning based on improved artificial potential field method[J].Aerospace,2023,10(6):562.
[17] CHEN Y D,WANG P L,LIN Z C,et al.Global path guided vehicle obstacle avoidance path planning with artificial potential field method[J].IET Cyber-Systems and Robotics,2023,5(1):e12082.
[18] ZHU Z X,YIN Y,LYU H G.Automatic collision avoidance algorithm based on route-plan-guided artificial potential field method[J].Ocean Engineering,2023,271:113737.
[19] LIU W,QIU K,YANG X F,et al.COLREGS-based collision avoidance algorithm for unmanned surface vehicles using modified artificial potential fields[J].Physical Communication,2023,57:101980.
[20] 谢春丽,高胜寒,孙学志.融合改进A*算法和贝塞尔曲线优化的路径规划算法[J].重庆理工大学学报(自然科学),2022,36(7):177-187.XIE C L,GAO S H,SUN X Z.Path planning algorithm combining improved A* algorithm and Bezier curve optimization[J].Journal of Chongqing University of Technology (Natural Science Edition),2022,36(7):177-187.(in Chinese)
[21] 陈德童,刘贤达,刘生伟.基于双向搜索改进A*算法的自动导引车路径规划[J].计算机应用,2021,41(sup 2):309-313.CHEN D T,LIU X D,LIU S W.Path planning of AGV based on improved A* algorithm of bidirectional search[J].Journal of Computer Applications,2021,41(sup 2):309-313.(in Chinese)
[22] 王中玉,曾国辉,黄勃.基于改进双向A*的移动机器人路径规划算法[J].传感器与微系统,2020,39(11):141-143,147.WANG Z Y,ZENG G H,HUANG B.Mobile robot path planning algorithm based on improved bidirectional A* star[J].Transducer and Microsystem Technologies,2020,39(11):141-143,147.(in Chinese)
[23] YU H M,NING L Q.Coordinated obstacle avoidance of multi-AUV based on improved artificial potential field method and consistency protocol[J].Journal of Marine Science and Engineering,2023,11(6):1157.
[24] WU D H,WEI L S,WANG G L,et al.APF-IRRT*:an improved informed rapidly-exploring random trees-star algorithm by introducing artificial potential field method for mobile robot path planning[J].Applied Sciences,2022,12(21):10905.
[25] LISANG L,BIN W,HUI X.Research on path-planning algorithm integrating optimization A-star algorithm and artificial potential field method[J].Electronics,2022,11(22):3660.