鱼类经过上亿年的进化,发展成具有很强的感知能力和灵活机动性及卓越的水下运动能力,以应对周围环境的自然和非自然变化[1]。鲹科推进模式作为鱼类的主要运动方式,推进速度快,主要依靠尾鳍反复波动致使流体流场发生一系列变化,从而产生鱼类机动运动所需动量[2]。因此,对鲹科推进模式的鱼类运动机理研究,有助于揭示鱼类的适应性进化、捕食策略和栖息地利用等方面的生态学特征。
粒子图像测速技术(particle image velocimetry,PIV)是通过非接触直接测量瞬时流场中互相关区域粒子的位移[3],进而得到流场速度的方法[4]。近年来,随着PIV各组成系统的改进完善,其逐渐成为流体流场测量的主要手段。Keane等[5]首次将PIV技术应用到流体力学研究中,从分辨率、检测率和准确性方面分析了自相关方法和互相关方法在处理图像中的优异,发现通过调节互相关参数可以消除自相关产生的信号偏差。Lauder[6]利用数字粒子图像测速技术(digital particle image velocimetry,DPIV)技术对具有同尾叶形态的蓝鳃太阳鱼(Lepomis macrochirus)在稳定游泳过程中的尾鳍功能进行试验研究,结果表明,背腹叶在鱼类稳定游动时可产生不同的力和扭矩。Nauen等[7]发现,鲭(Scomber japonicus)尾流产生一系列椭圆形涡环。Tytell等[8]分析了蓝鳃太阳鱼身体、背鳍和臀鳍产生的流动模式在逃逸反应中的作用。老轶佳[2]以振动板推进理论为基础,研究了不同尾鳍及摆动参数对尾涡流场结构的影响,发现柔性尾鳍比刚性尾鳍具有更高的推进效率。敬军等[9]研究了鲫(Carassius auratus)逃逸反应过程中发生C型起动(即鱼类通过迅速地使其身体弯曲成“C”形后回摆,从而实现快速转弯的一种机动运动[10])的特征。吴燕峰等[11]研究了斑马鱼(Danio rerio)从低速巡游状态做出捕食反应的运动过程中发生S型起动(即鱼体由静止或者稳态游动中突然呈“S”形后迅速转向目标方向,接着尾部大幅度摆至垂直于鱼体中线位置,到达目标方向后,鱼体由弯曲状态恢复为游动状态的一种机动运动[12])的特征。余英俊等[13]利用PIV技术计算了拉萨裸裂尻鱼(Schizothorax richardsonii)在自由游泳状态下的压力分布,结果表明,在尾部凹陷处流体压力为负值,凸起处为正值。Mwaffo等[14]对斑马鱼在微型隧道中的游泳力学进行研究,发现鱼类爆发运动时身体附近会产生一对符号相反的涡旋。张永年等[15-16]利用PIV技术和涡量分析原理,对草鱼(Ctenopharyngodon idella)幼鱼力学特征分析发现,草鱼幼鱼在直线游泳和转弯状态下的动力来源主要来自尾部,后退游泳时主要依靠胸鳍推进。陈宏等[17]根据鲫C型起动图像序列,建立C型起动运动学方程,发现C型起动仿生机器人具有高机动性。从上述研究可以看出,前期对运动鱼体流场的测量,从最初简单地提取运动学数据,到目前通过涡量场、压力场量化流场产生水动力数据,但由于涡旋的复杂性和测量的困难性,所以目前主要通过压力场研究流体力学[18]。
草金鱼(Carassius auratus)幼鱼隶属于鲤科鱼类,是金鱼的原始类型,其采用鲹科推进模式,在水中游动异常迅速[19],是最常见的观赏鱼类之一。本研究中,以草金鱼幼鱼为研究对象,基于简易的PIV装置和涡量矩定理,追踪草金鱼幼鱼机动转弯运动轨迹,分析草金鱼幼鱼转弯时的运动学及动力学特征,以期为探究鱼类运动行为、鱼群机动行为提供基础数据,并为鱼类运动机理研究及水下仿生模型设计提供参考。
1 材料与方法
1.1 材料
1.1.1 试验鱼 2022年8月13日从上海海洋大学实验楼B楼108实验室鱼缸中选取50尾体长为5~8 cm的草金鱼幼鱼,于水温为18 ℃、溶解氧为8 mg/L的鱼缸中暂养24 h后进行试验,暂养期间不投喂饲料。
1.1.2 试验装置 试验装置包括试验鱼缸和一套PIV系统(图1)。鱼缸长×宽×高为24 cm×24 cm×20 cm,水深2 cm,刚好淹没整个鱼体,试验用水为纯净水。PIV系统由光源系统、图像拍摄系统、同步系统和矢量计算系统组成[20]。其中,光源系统采用绿色激光(波长为 510~515 nm),在试验缸中撒入中性PSP(polyamide seeding particles)示踪粒子,粒径为50 μm,密度为1.03~1.05 g/cm3,示踪粒子密度接近于水的密度,容易漂浮在水体表面,为了破坏其表面张力,在流场中加入表面活性剂,使得PSP示踪粒子与水体混合均匀,且示踪粒子的斯托克斯数小于0.01,具有良好的跟随性[21]。图像采集系统主要由高速相机和片光源组成[20],相机布放在鱼缸正上方(空间分辨率为1 085×690 pixel),以拍摄幼鱼游动的图像。草金鱼幼鱼放入试验鱼缸后,待其在新环境中适应一段时间再进行试验视频拍摄;同时为了防止其他光源的干扰,整个试验在黑暗无光的环境中进行,并调节激光位置及激光发射方向,在幼鱼尾叉处形成片光源[6],由于鱼体的反光,导致鱼体周围的部分粒子被遮挡,会造成一定的试验误差。同步系统控制激光器和相机协调运作,确保拍摄到草金鱼幼鱼转弯的全过程。矢量计算系统是通过PIVlab后处理包对两次曝光粒子图像提取速度场数据[18],间接得到其他动力学数据和力学数据。
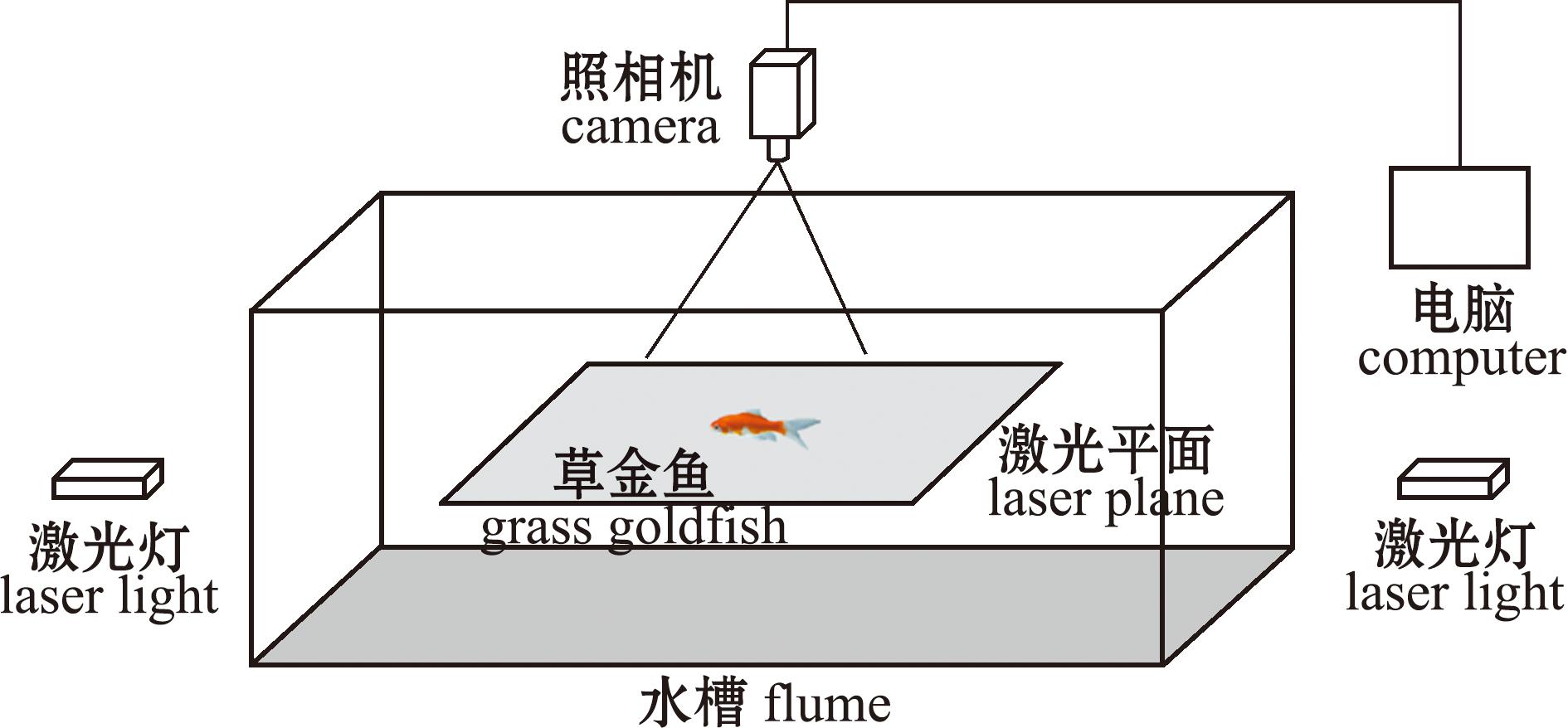
图1 流场测试PIV系统
Fig.1 PIV system in flow field test
1.2 方法
通过试验获得草金鱼幼鱼原始视频帧,并用PIVlab_GUI.m图像处理工具进行处理,PIVlab是在MATLAB R2021a中编程的开源数字PIV后处理包[22]。为了便于分析,将鱼体发生偏转至偏转完成定义为一次转弯运动T,追踪鱼体尾部4个参考点[14],记为n1、n2、n3、n4(图2(a))。在整个转弯过程中,相邻两帧图像时间间隔较短,可以假设鱼体在这一时间段内各参考点以恒定加速度运动[10]。
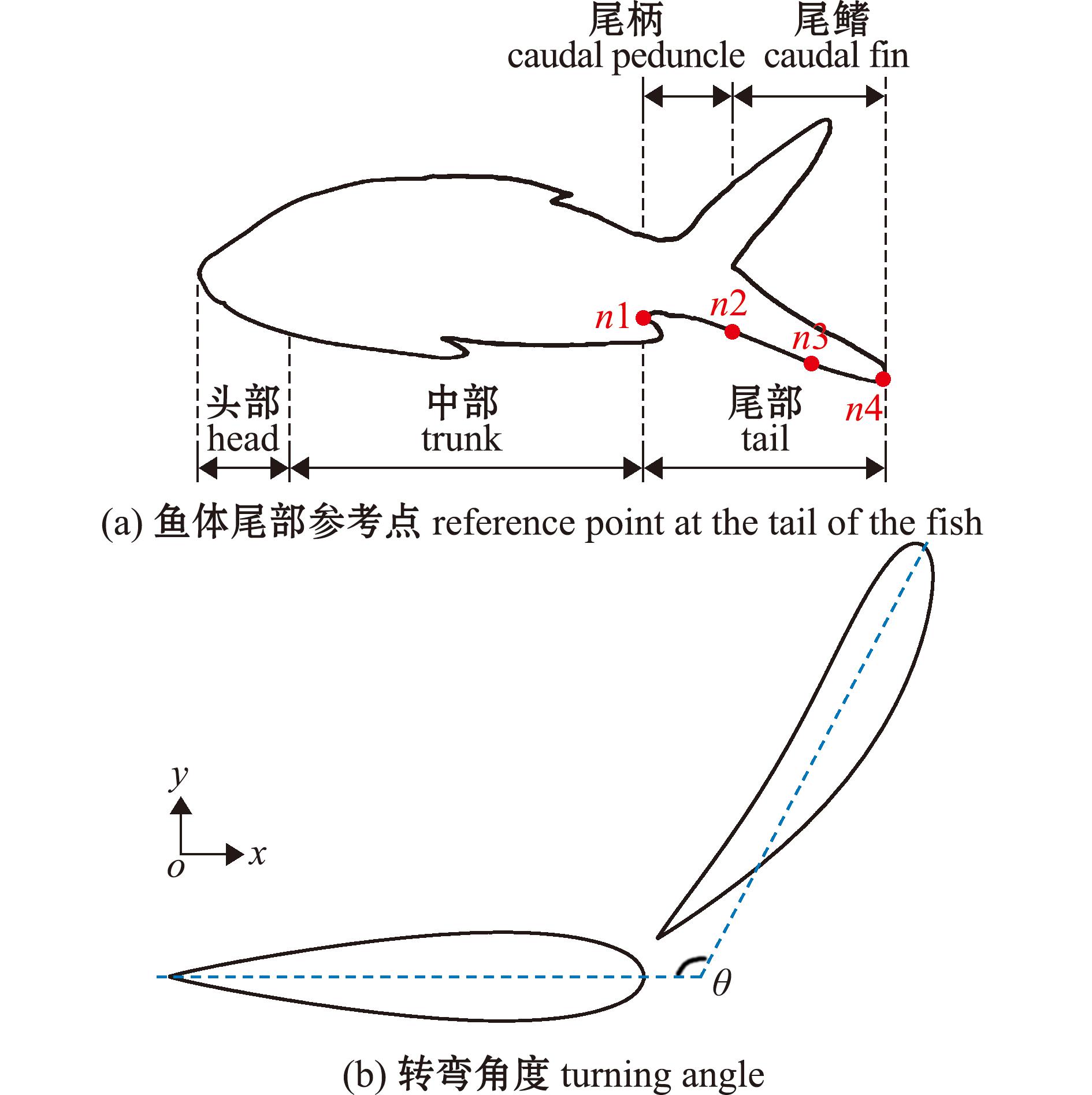
图2 草金鱼幼鱼尾部参考点及转弯角度
Fig.2 Reference point and turning angle of the tail of the grass golden fish
1.2.1 粒子图像的选取 选取体长和质量非常相近的50尾草金鱼幼鱼进行试验,通过观察发现,不同个体的幼鱼在试验缸中适应一段时间后,运动轨迹相似,故本研究中选取体长为6.55 cm的草金鱼幼鱼作为试验代表,重复拍摄45 min。试验过程中发现,幼鱼经常发生转弯,且大转弯发生的概率占总转弯的80%以上。处理视频帧图像时还发现,运动轨迹相似的情况下,尾鳍摆动周期、位移等运动学数据及作用力等水动力学数据相差不大,因此,从中选取两个大转弯角度(117°、123°)相近的转弯图像序列进行分析比较,结论具有普遍意义[14]。对比发现,两种大角度转弯下幼鱼的转弯方向及鱼体形态会发生不一样的变化,故将转弯过程分别记为T1、T2;每种转弯过程选取一个运动周期内相同时间间隔的19张图像用PIVlab.GUI.m进行处理,从中选择7张图像(图3)进行进一步分析,每两张图像的时间间隔为33.33 ms。

图3 一个周期内两种类型的转弯过程
Fig.3 Two types of turning processes in one cycle
1.2.2 运动学测量 鱼类转弯过程中,转弯角度θ是指草金鱼幼鱼起与止位置之间发生的偏转角度[23]。利用图像融合将鱼体二维轮廓和示踪平面进行分割,再利用曲线拟合工具分析坐标数据并提取中线(图2(b))。其分割过程表达式[24]如下:
Dst=src1×alpha+src2×beta+gamma。
(1)
式中:Dst表示输出的目标图像;src1和src2分别表示进行图像融合的背景图像和前景图像;alpha为权重1,beta为权重2,两个权重控制着图像的融合比例;gamma为图像的偏移量,通过改变像素gamma的值,图像会呈现偏白或偏黑的效果。
鱼类弯曲系数(βb)用于量化全身曲率,是衡量鱼类弯曲程度的指标,其计算公式[25]为
βb=1-Lc/Lb。
(2)
式中:Lc为吻端至尾鳍末端的弦长;Lb为体长。
1.2.3 力学计算原理 涡量作为反映流体涡旋常用的运动学参数,是指流体有旋运动产生的旋度,通过测量速度场的数学旋度计算得到[26-27],计算公式为
(3)
式中:ω代表涡量(s-1);u、v分别为粒子的水平速度和竖直速度(m/s)。
在二维情况下,基于涡量矩定理,流场对幼鱼的作用力可表示为[28]
![]()
(4)
式中:n为鱼体表面单位法向量;x为横坐标;y为纵坐标;li为鱼体流场边界;Sb为鱼体所占区域。
鱼类转弯过程中,涡流强度使鱼类转动,产生的力矩计算公式为
τ=Γ×D。
(5)
式中:τ为力矩(mN/m);D是鱼体到力作用线的垂直距离(m);Γ为速度环量(m2/s)。
速度环量是通过围绕涡环等值线上的切向速度对其合速度V做线积分,表达式如下[14]:
(6)
式中,dt为曲线t的弧元素矢量。
2 结果与分析
2.1 一般运动学特征
草金鱼幼鱼在转动过程中,鱼体和流体相互作用,致使鱼体形态结构发生变化。T1类型的转弯过程中,鱼类头部和尾部向一侧弯曲,鱼体形态呈C型结构变化(图3(a))时,转弯过程中横向偏移量为(1.22±0.09)cm,侧向偏移量为(3.40±0.09)cm,βb为0.09。T2类型的转弯分为两个阶段(图3(b)):第一阶段,持续时间较短,占整个周期的1/3,鱼体头部向一侧弯曲,身体中后部向另一侧弯曲,随着时间的变化后部弯曲曲率明显变小,总体上鱼体形态呈S型结构状态;第二阶段,身体中后部与头部向同一侧弯曲,鱼类转弯方向发生变化,鱼体形态呈C型结构状态。T2类型的整个转弯过程中横向偏移量为(3.38±0.09)cm,侧向偏移量为(5.63±0.09)cm,βb为0.06。
两种类型的转弯过程中,整个转弯摆动周期速度呈波动分布,大小存在差异。T1平均速度为0.130 7 m/s,各参考点速度分布相对离散,集中分布于较小值,n3点的速度变化幅度较小(图4);各参考点的水平速度分布较集中,n4点的水平速度变化幅度较大(图5);各参考点的垂直速度分布相对集中且相差不大,起始阶段n1点的垂直速度变化趋势与其他参考点相反(图6)。
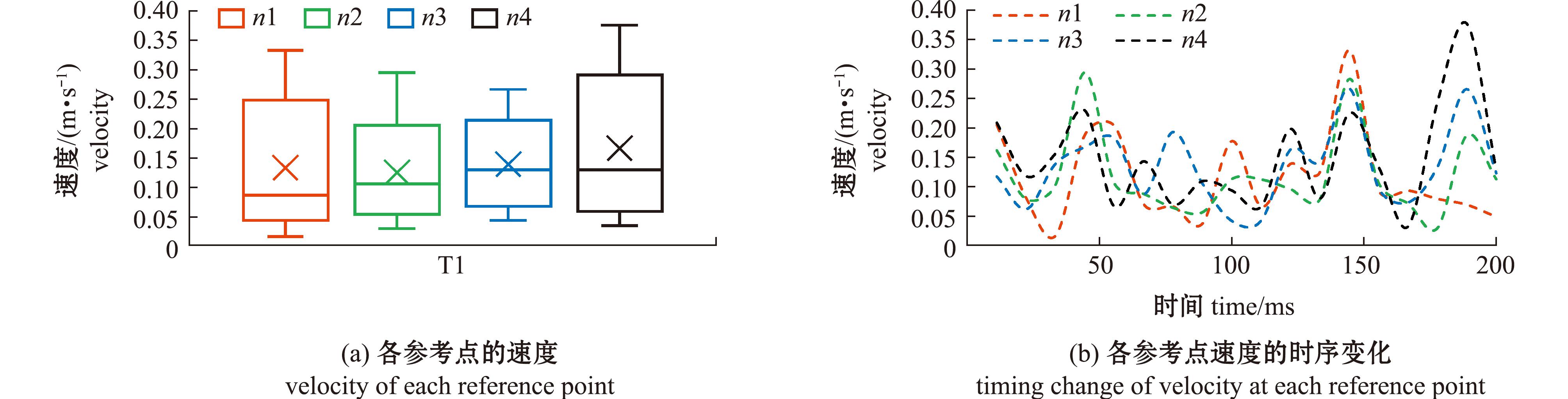
图4 T1类型转弯过程中各参考点的速度及时序变化
Fig.4 Velocity and time sequence of each reference point during T1 turn
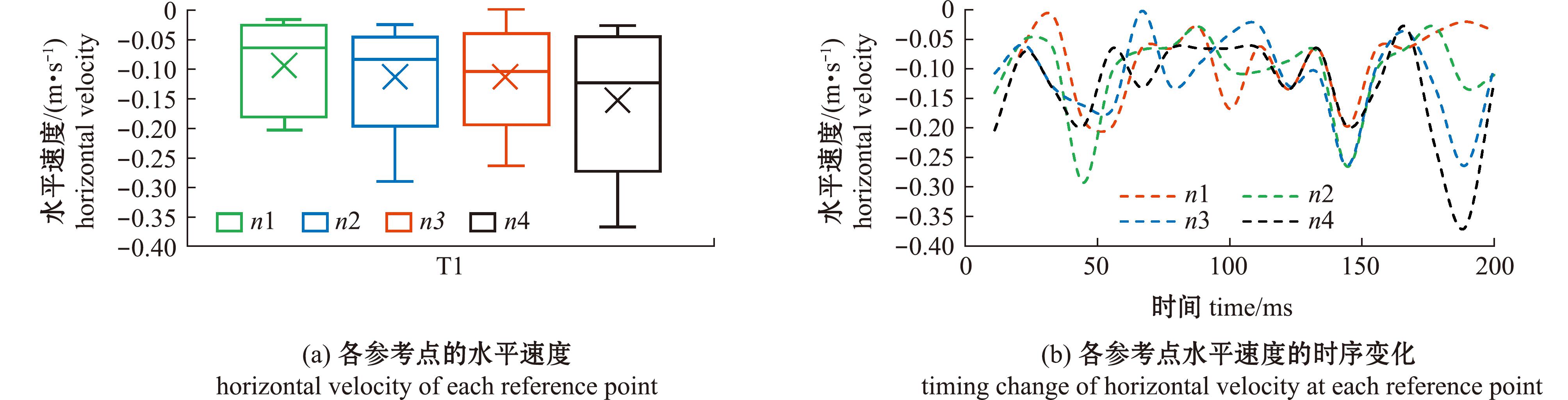
图5 T1类型转弯过程中各参考点的水平速度及时序变化
Fig.5 Horizontal velocity and time sequence change of each reference point during T1 turn

图6 T1类型转弯过程中各参考点的垂直速度及时序变化
Fig.6 Vertical velocity and time sequence of each reference point during T1 turn
T2平均速度为0.104 4 m/s,n1、n4点的速度分布范围相对离散,集中分布于较小值,n2、n3点的速度分布相对平衡且较集中,n1点的速度变化幅度大于其他参考点(图7);各参考点的水平速度整体上呈先减小后增加的趋势,n4点的水平速度明显大于其他参考点(图8);各参考点的垂直速度主要集中于较大值,n2点的垂直速度变化幅度较小(图9)。
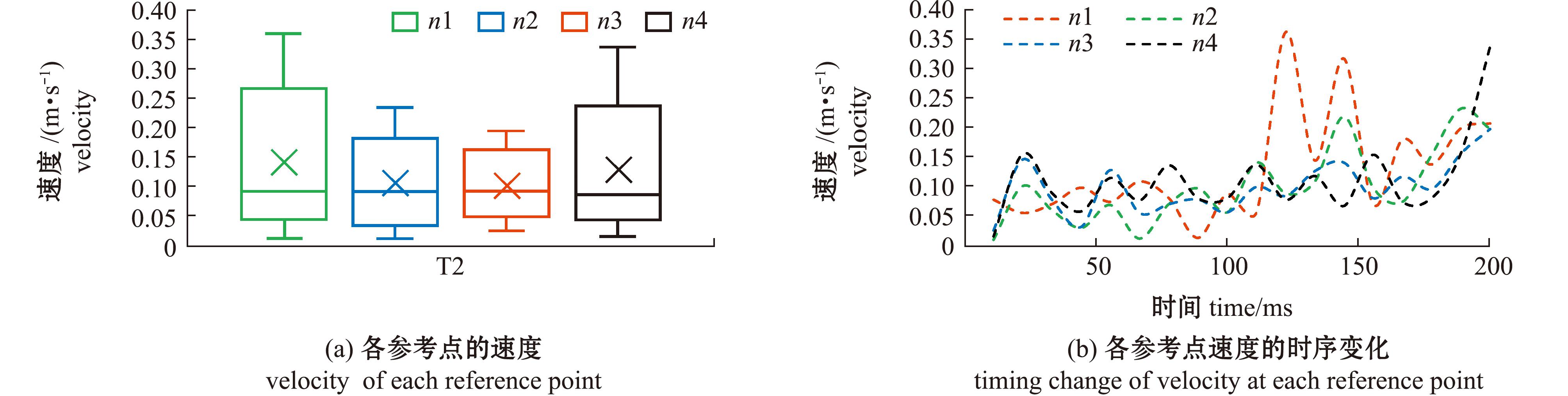
图7 T2类型转弯过程中各参考点的速度及时序变化
Fig.7 Velocity and time sequence of each reference point during T2 turn
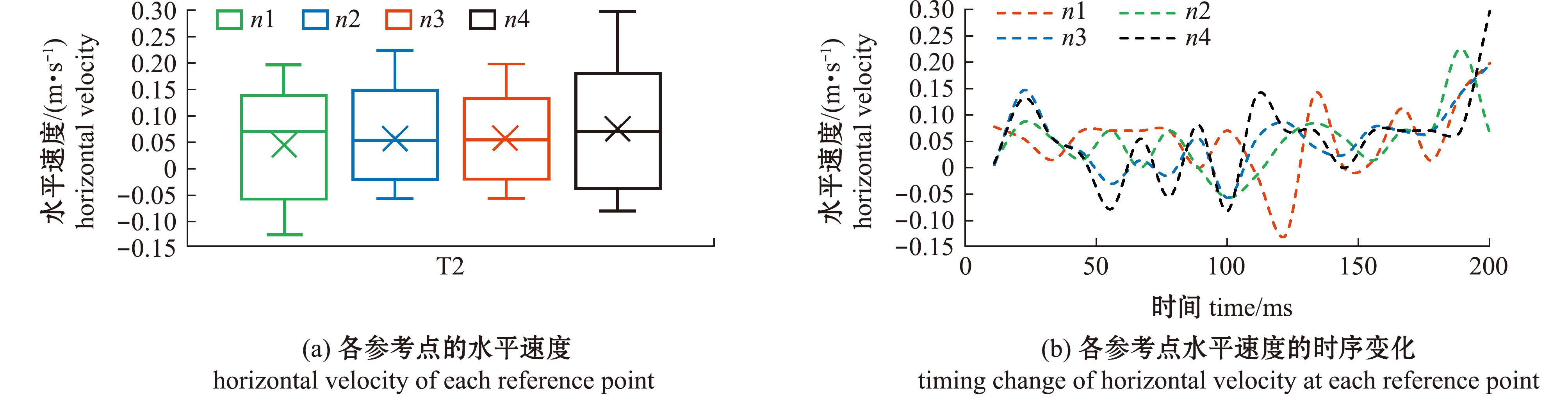
图8 T2类型转弯过程中各参考点的水平速度及时序变化
Fig.8 Horizontal velocity and time sequence change of each reference point during T2 turn
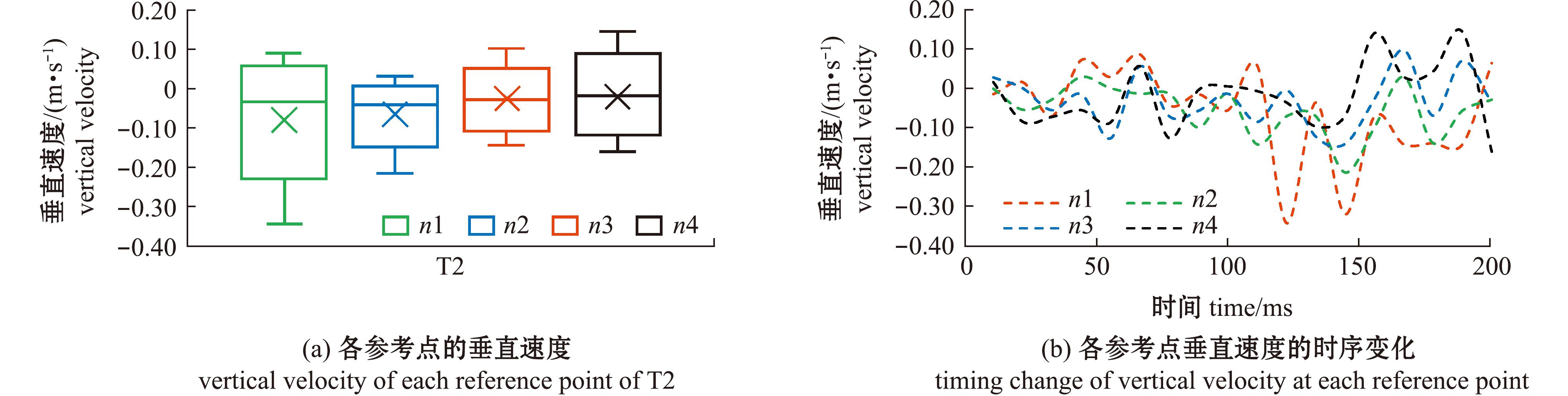
图9 T2类型转弯过程中各参考点的垂直速度及时序变化
Fig.9 Vertical velocity and time sequence of each reference point during T2 turn
2.2 涡量分布特征
观察草金鱼两种类型转弯过程发现,鱼体尾部周围涡量分布存在异同;T1在0~199.98 ms,T2在0~33.33 ms时,鱼头处形成体艏尾流,以负值涡量为主,T2在33.33~199.98 ms时,鱼头处以正值涡量为主;T2在0~33.33 ms时,鱼体形态呈S型结构变化,转弯侧主要以正值涡量为主,对角侧以负值涡量为主;T1在0~166.65 ms,T2在33.33~166.65 ms时,鱼体形态呈C型结构变化,转弯侧以负值涡量为主,对角侧以正值涡量为主,涡环形成、聚集并脱落;T1、T2在166.65~199.98 ms时,转弯侧以正值涡量为主,对角侧以负值涡量为主(图10)。
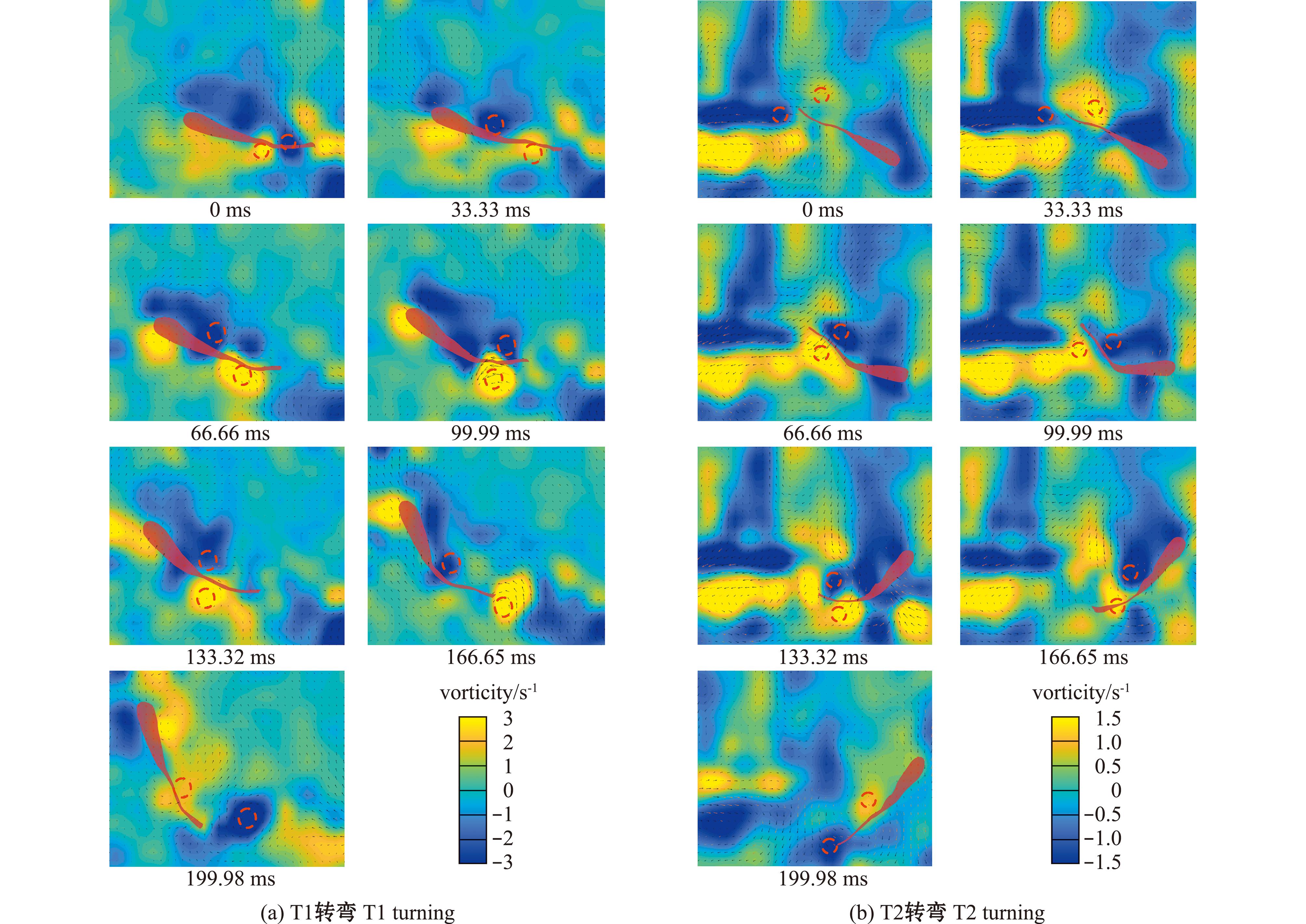
黄色代表正值涡量,蓝色代表负值涡量,箭头方向代表速度矢量方向。
Yellow represents positive vorticity,blue represents negative vorticity,and arrow direction represents velocity vector direction.
图10 两种类型转弯过程中幼鱼尾部周围流场涡量云图的变化
Fig.10 Changes in the vortices map around the tail of juvenile fish during two types turns
草金鱼幼鱼在T1和T2两种类型机动转弯过程中,幼鱼尾部周围流体涡量随尾鳍摆动变化也呈现一定规律。 T1和T2两种转弯过程中鱼体尾部流场正值涡量变化趋势相同,但T2类型转弯前期,鱼体形态呈S型结构变化,尾部流场负值涡量大于鱼体形态只呈C型结构变化的转弯过程T1产生的涡量且变化趋势相反,随后T1和T2产生的流场涡量呈相同变化趋势;整个转弯过程中,T1产生的流场涡量大于T2(图11)。

图11 两种类型转弯过程中幼鱼尾部周围的涡量
Fig.11 The amount of vorticities around the tail of juveniles during two types turns
2.3 动力学特征
本研究中,计算了两种类型转弯运动过程中4个参考点作用力的大小。T1、T2类型转弯过程中产生的作用力在尾部呈波动分布,T1产生的作用力大于T2,T1的波动范围较大,产生的正作用力为2.06~133.49 mN,产生的负作用力为-83.85~-2.15 mN;T2产生的作用力相对集中,正作用力为24.06~80.95 mN,负作用力为-59.60~-5.86 mN(图12)。结合图11和图12发现,力和涡量之间有明显的相关性,其大小和涡量呈正相关,涡量越大,产生的作用力就越大。计算得到,整个转弯过程中,T1产生的转矩为0.072 2 mN/m,T2产生的转矩为0.042 4 mN/m。
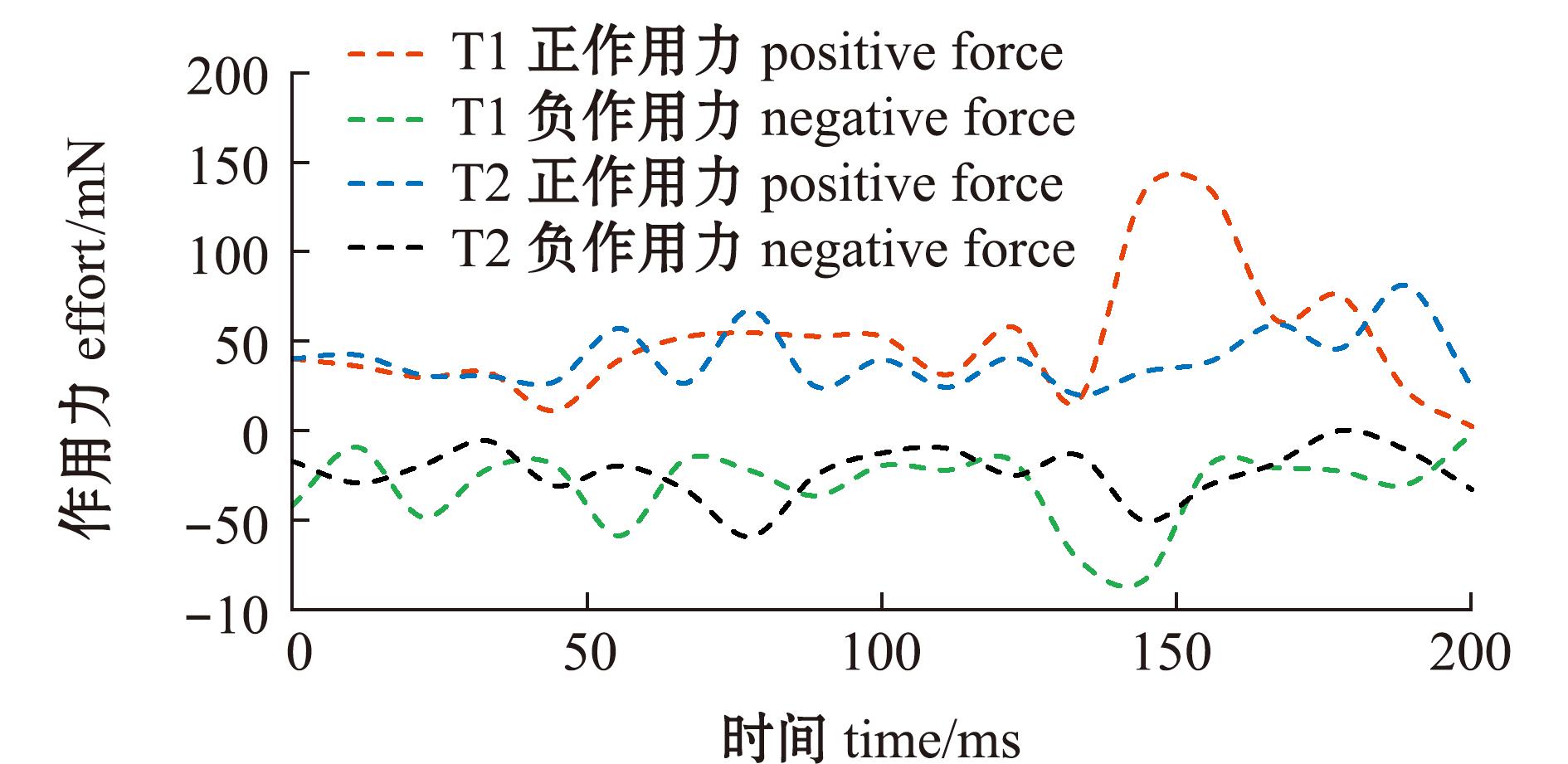
图12 两种转弯过程中流体对幼鱼尾部的作用力
Fig.12 The force of the fluid on the tail of the juvenile fish during two types turns
3 讨论
3.1 不同转弯状态下草金鱼运动学比较
图像的选取对于解析鱼类转弯运动机制至关重要。本研究中,采用的相机帧率相对较小,故选取草金鱼幼鱼转弯运动图序时,整个转弯时间的选择相对较长。同时为了控制幼鱼尾叉保持在激光平面上,降低了水平面高度,造成一定的边界效应。转弯是鱼类常见的机动运动,本研究中分析草金鱼幼鱼转弯运动机理时主要发生大角度转动。Thandiackal等[23]研究发现,斑马鱼爆发-滑行机动运动后,转弯角度一般小于70°,而本研究中是基于前进运动发生转弯,这表明鱼类转弯前的运动状态影响鱼类转弯运动学特性,更详细的影响有待进一步研究。侧向偏移量和弯曲曲率影响鱼类转弯的机动性[25],较高的弯曲曲率和侧向偏移量更有利于鱼类稳定的转弯。张永年等[15]研究体长6.3 cm的草鱼时发现,侧向偏移量为2.30 cm,相关转弯水动力学参数小于草金鱼幼鱼。草金鱼作为观赏鱼类,大多饲养在体积较小的水族箱内,除休息不动的时间,大多时间都在养殖水缸中游动,其具有很强的灵活性。本研究中发现,T1类型转弯过程产生的侧向偏移量小于T2产生的侧向偏移量,可能是由于鱼体转向结构造成的,C型结构转动更能让草金鱼保持稳定以防止较大的侧向偏移。
游泳速度会影响鱼类转弯水动力学。本研究中发现,鱼类转弯时形态呈C型结构弯曲的相关速度大于S+C型结构相结合弯曲的速度。通过观察鱼体形态呈S+C型结构转弯时发现,鱼类做出类似逃跑的动作,由此推测,形态呈C型结构转弯主要用于鱼类的逃逸反应,为躲避敌害,鱼类快速起动,促使鱼类形态弯曲为C型结构,改变鱼类运动方向,随后鱼类以较大的速度完成转弯,之后回摆至平直状态。Gazzola[29]对幼鱼逃逸反应的研究发现,C型结构弯曲有利于促进鱼类逃逸。S型结构弯曲主要用于攻击和捕食猎物[30],但本研究中鱼体形态呈S+C型结构转弯速度相对较小,推测这种转弯方式主要用于求偶、避开障碍物,利用S型结构弯曲规划路径,快速改变鱼类运动方向,从第二阶段开始幼鱼尾鳍速度在恒定范围内波动,改变鱼类运动方向,形态呈C型结构变化。综上,为应对不同的环境变化,鱼体形态结构会发生相应的变化。
3.2 不同转弯状态下幼鱼尾部周围涡量变化
涡量在描述鱼类转弯运动状态形态结构变化中起着至关重要的作用[16]。通过分析流场内涡量的变化,量化鱼类尾鳍水动力学,有助于了解鱼类的转弯机制[15]。本研究中发现,草金鱼幼鱼转弯过程中,前半个周期,鱼头部处主要为负值涡量,产生了强大吸力区,与相关研究结果一致[23,27],可能是为了控制鱼体前部在转弯过程中的稳定性及帮助控制转弯方向;后半个周期,鱼头部处产生负值涡量,可能是由于身体前部在加速时将流体推向一侧,减速时要过渡到被流体拉动的结果[23],尾柄正值涡量控制幼鱼完成偏转。此外,鱼类转弯过程中,转弯侧的负值涡量可减少阻力,减少能量消耗,正值涡量可改变鱼类运动方向并产生鱼类前进所需推进力,而鱼类转弯的最后时段,转弯侧和对角侧涡量发生变化,是由于转弯完成,鱼类要为下一运动状态做准备并产生新的涡量[15]。因此,鱼体周身正负涡流交替出现,协同控制鱼类机动转弯。
3.3 不同转弯状态下幼鱼尾部周围动力学特征
当转动角度相近时,不同的转弯类型及转弯动机对于鱼类机动作用力产生显著影响。本研究中发现,鱼体形态只发生C型结构变化时会产生更大的作用力。张冰冰[30]发现,鱼体形态发生S型结构变化时,产生较小的作用力和扭矩,间接影响S+C型结构转弯,产生较小的水动力。杨国党等[27]研究表明,幼鱼尾鳍周围的正值涡量是幼鱼作用力产生的主要来源。本研究中,正值涡量产生的作用力大于负值涡量。Tytell等[31]发现,鱼体周围涡量的大小和推进力的大小呈正相关,涡量较大,其受力越大,这与本研究结果一致。这说明草金鱼幼鱼机动转弯过程中,同一时刻尾部各参考点涡量方向相同,涡量越大,传递给流体的动量越大,产生鱼体改变方向的转动力就越大。本研究中,鱼体形态呈C型结构机动转弯产生较大的力矩,这也证明了鱼体形态呈C型结构机动转弯可用于机敏性较强的逃逸反应。
4 结论
1)鱼体形态结构变化影响鱼类机动,鱼体呈C型结构转弯运动学特性明显优于S+C型结构转弯。
2)鱼体不同形态结构变化下,机动转弯的目的不同,尾部周围涡量分布也不尽相同。尾部正值涡量主要促使鱼类转弯,负值涡量主要控制鱼类机动转弯的方向。
3)鱼体形态呈C型和S+C型两种类型的转弯过程中,动力学差异明显,不同转弯类型产生作用力峰值的时刻不同。
[1] 李林.鲹科鱼类游动力学特性的理论与仿真研究[D].哈尔滨:哈尔滨工业大学,2008.
LI L.The theory and simulink research of thunniform fish’s swimming mechanic characteristic[D].Harbin:Harbin Institute of Technology,2008.(in Chinese)
[2] 老轶佳.基于DPIV技术的摆动尾鳍流场特性研究[D].镇江:江苏科技大学,2009.
LAO Y J.Research on flow field characteristics of oscillating caudal fin based on DPIV technology[D].Zhenjiang:Jiangsu University of Science and Technology,2009.(in Chinese)
[3] DEEN N G,WESTERWEEL J,DELNOIJ E.Two-phase PIV in bubbly flows:status and trends[J].Chemical Engineering &Technology,2002,25(1):97.
[4] SALMAN H E,YALCIN H C.Advanced blood flow assessment in Zebrafish via experimental digital particle image velocimetry and computational fluid dynamics modeling[J].Micron,2020,130:102801.
[5] KEANE R D,ADRIAN R J.Theory of cross-correlation analysis of PIV images[J].Applied Scientific Research,1992,49(3):191-215.
[6] LAUDER G V.Function of the caudal fin during locomotion in fishes:kinematics,flow visualization,and evolutionary patterns[J].Integrative and Comparative Biology,2000,40(1):101-122.
[7] NAUEN J C,LAUDER G V.Hydrodynamics of caudal fin locomotion by chub mackerel,Scomber japonicus (Scombridae)[J].The Journal of Experimental Biology,2002,205(Pt 12):1709-1724.
[8] TYTELL E D,LAUDER G V.Hydrodynamics of the escape response in bluegill sunfish,Lepomis macrochirus[J].The Journal of Experimental Biology,2008,211(Pt 21):3359-3369.
[9] 敬军,李晟,陆夕云,等.鲫鱼C形起动的运动学特征分析[J].实验力学,2004,19(3):276-282.
JING J,LI S,LU X Y,et al.The kinematic analysis of C-start in crucian carp (Carassius auratus)[J].Journal of Experimental Mechanics,2004,19(3):276-282.(in Chinese)
[10] 张冰冰,余永亮.斑马鱼C型起动中动力学特性的活体实验研究[J].实验力学,2014,29(6):727-736.
ZHANG B B,YU Y L.Living body experimental study of dynamic characteristics of zebrafish C-start swimming[J]. Journal of Experimental Mechanics, 2014,29(6):727-736. (in Chinese)
[11] 吴燕峰,贾来兵,尹协振.斑马鱼S型起动运动学研究[J].实验力学,2007,22(5):519-526.
WU Y F,JIA L B,YIN X Z.The kinematic analysis of S-start of Zebra danio(Danio rerio)[J].Journal of Experimental Mechanics,2007,22(5):519-526.(in Chinese)
[12] 吴正兴,喻俊志,苏宗帅,等.仿生机器鱼S形起动的控制与实现[J].自动化学报,2013,39(11):1914-1922.
WU Z X,YU J Z,SU Z S,et al.Control and Implementation of S-start for a Multijoint Biomimetic Robotic Fish[J].Acta Automatica Sinica,2013,39(11):1914-1922. (in Chinese)
[13] 余英俊,胡晓,石小涛,等.基于PIV的拉萨裸裂尻摆尾压力场特征分析[J].实验力学,2019,34(2):289-300.
YU Y J,HU X,SHI X T,et al.Analysis on the pressure field characteristics of Schizopygopsis younghusbandi Regan tail swinging based on PIV[J].Journal of Experimental Mechanics,2019,34(2):289-300.(in Chinese)
[14] MWAFFO V,ZHANG P,ROMERO CRUZ S,et al.Zebrafish swimming in the flow:a particle image velocimetry study[J].PeerJ,2017,5:e4041.
[15] 张永年,胡晓,余英俊,等.基于涡量原理的草鱼幼鱼力学特性研究[J].实验力学,2020,35(5):915-924.
ZHANG Y N,HU X,YU Y J,et al.Study on mechanical characteristics of grass carp juveniles based on vorticity method[J].Journal of Experimental Mechanics,2020,35(5):915-924.(in Chinese)
[16] 张永年.基于涡量原理的草鱼幼鱼游泳行为及其动力学特性研究[D].宜昌:三峡大学,2020.
ZHANG Y N.Study on swimming behavior and dynamics of juvenile grass carps based on vorticity principle[D].Yichang:China Three Gorges University,2020.(in Chinese)
[17] 陈宏,竺长安,尹协振,等.仿鱼机器人C形起动的动力学分析[J].哈尔滨工业大学学报,2009,41(1):113-117.
CHEN H, ZHU C A,YIN X Z,et al.Dynamic analysis on c-start swimming of fish-like robot[J].Journal of Harbin Institute of Technology,2009,41(1):113-117.(in Chinese)
[18] 张奔,胡晓,杨国党,等.基于压力场的草鱼幼鱼巡游动力学研究[J].水力发电学报,2021,40(6):79-88.
ZHANG B,HU X,YANG G D,et al.Hydrodynamics of juvenile grass carp(Ctenopharyngodon idellus) in steady swimming based on pressure field[J].Journal of Hydroelectric Engineering,2021,40(6):79-88.(in Chinese)
[19] 天山雪.金鱼的十种尾型[J].水族世界,2010(5):138-147.
TIAN S X.Ten tail types of gold fish[J].Aquarium,2010(5):138-147.(in Chinese)
[20] 孔维波.PIV技术的应用与发展[J].山东化工,2019,48(6):115-119.
KONG W B.Application and development of PIV[J].Shandong Chemical Industry,2019,48(6):115,119.(in Chinese)
[21] DRING R P.Sizing criteria for laser anemometry particles[J].Journal of Fluids Engineering,1982,104(1):15-17.
[22] THIELICKE W,STAMHUIS E J.PIVlab-towards user-friendly,affordable and accurate digital particle image velocimetry in MATLAB[J].Journal of Open Research Software,2014,2(1):335-347.
[23] THANDIACKAL R,LAUDER G V.How zebrafish turn:analysis of pressure force dynamics and mechanical work[J].The Journal of Experimental Biology,2020,223(Pt 16):jeb223230.
[24] GUPTA G.Algorithm for image processing using improved median filter and comparison of mean,median and improved median filter[J].Blue Eyes Intelligence Engineering &Sciences Publication,2011,1(5):2231-2307.
[25] HAWKINS O H,ORTEGA-JIMÉNEZ V M,SANFORD C P.Knifefish turning control and hydrodynamics during forward swimming[J].The Journal of Experimental Biology,2022,225(7):jeb243498.
[26] DABIRI J O,COLIN S P,KATIJA K,et al.A wake-based correlate of swimming performance and foraging behavior in seven co-occurring jellyfish species[J].The Journal of Experimental Biology,2010,213(Pt 8):1217-1225.
[27] 杨国党,胡晓,张奔,等.基于粒子图像测速技术(PIV)的自由游泳草鱼动力学特征分析[J].大连海洋大学学报,2021,36(5):833-841.
YANG G D,HU X,ZHANG B,et al.Analysis of hydrodynamic characteristics of grass carp Ctenopharyngodon idellus juveniles under free-swimming status based on Particle Image Velocimetry (PIV)[J].Journal of Dalian Ocean University,2021,36(5):833-841.(in Chinese)
[28] 马明.基于涡量场的二维物体非定常气动力计算[D].上海:上海交通大学,2012.
MA M.Calculation of the unsteady aerodynamics based on two dimensional vorticity field[D].Shanghai:Shanghai Jiao Tong University,2012.(in Chinese)
[29] GAZZOLA M,VAN REES W, KOUMOUTSAKO S.C-start: optimal start of larval fish[J]Journal of Fluid Mechanics, 2012,698: 5-18.
[30] 张冰冰.斑马鱼机动运动的水动力学实验研究[D].北京:中国科学院大学,2014.
ZHANG B B.Experimental study on hydrodynamics of zebrafish maneuvering[D].Beijing:University of Chinese Academy of Sciences,2014.(in Chinese)
[31] TYTELL E D,LAUDER G V.The hydrodynamics of eel swimming[J].Journal of Experimental Biology,2004,207(11):1825-1841.