在贸易全球化背景下,以航运业为主的国际贸易越来越繁忙。随着商船吨位的增加,操纵变得较困难;随着捕鱼业的发展,远洋捕捞活动明显增加。因此,海上商船与渔船相遇的概率增大,碰撞事故经常发生,而碰撞事故发生后商船的逃逸现象又对弱势渔船造成了更大的经济损失。
根据中华人民共和国海事局官网“事故教训”模块中公布的示例,船舶碰撞事故占所有事故的比例高达39.28%,而其中商船与渔船碰撞(以下简称“商渔船碰撞”)事故占据了较大部分。因此,研究船舶碰撞损伤特性,特别是商渔船碰撞时渔船的受损情况,并对渔船易损部位的加强方法提出建议,对维持海上运输安全、建立并完善相关法律法规、保护人民的生命财产安全、减少经济损失及保护海洋环境等都具有重大意义。船舶碰撞是非常复杂的非线性瞬态动力学问题,在不同的碰撞工况下,船舶受损特性是不同的。在实际航行环境中,船舶碰撞形式多种多样,根据船舶碰撞角度、碰撞时的航速、碰撞位置等不同情况,对船舶碰撞进行研究便产生了许多可能性。
船舶碰撞问题最早由Minorsky[1]提出,除了把碰撞中损失的动能认定是结构的变形能外,他还尝试将内部和外部碰撞力学分开进行研究。Pedersen[2]在研究外部碰撞力学时,利用切片理论求解船体的水动力载荷,梁文娟[3]将此方法扩展至三维碰撞。Motora[4]利用模型试验验证了在碰撞事件发生小于1 s时,可将附加质量设为恒定值。Pedersen等[5]在刚体碰撞问题上提出了新的二维机理求解办法。除以上研究外,其他学者对船体外部碰撞问题也进行了许多研究,这些研究推动了外部碰撞力学的发展。
内部碰撞力学主要研究船舶碰撞过程中的结构响应,其研究方法包括经验公式法、试验方法、数值计算法及解析法等。目前,国内外学者对内部碰撞力学已有较多研究。如刘敬喜等[6]分析了双层壳油船舷侧结构的耐撞性;刘昆等[7]分析了船用夹层板的防护性能;Haris等 [8]提出了一种解析计算方法,并利用LS-DYNA软件模拟了几种船舶碰撞场景,验证了解析计算方法的准确性;Ringsberg等[9]通过有限元方法探究了新型舷侧结构在碰撞过程中的耐撞性能;Ringsberg等[10]模拟了半球形撞头撞击舷侧外板的试验;Paik等[11]基于理想单元法(ISUM)提出了一种用于分析碰撞船舶船体结构损伤的方法。这些研究表明,有限元数值计算方法为船舶碰撞的模拟提供了极大的便利,目前已广泛应用于船舶碰撞问题的研究中。
本研究中,使用有限元数值仿真方法建立渔船全船有限元模型和商船球鼻艏有限元模型,并在有限元软件中对商船和渔船碰撞过程进行仿真模拟,得到渔船船体结构在碰撞中发生的变形、碰撞力及能量变化等规律,本研究结果不仅能为渔船结构优化设计提供理论指导,而且结合商船航行记录可为受害渔船索赔提供依据,还能为研究制定渔船在特定海域及航线上作业和航行的法规提供参考依据。
1 渔船全船与商船球鼻艏有限元建模
根据本研究中的研究目的,重点关注被撞船舶即渔船的受损情况,故对渔船全船进行建模。而对于撞击船,由于球鼻艏结构强度大,且本研究中不考虑球鼻艏的破坏情况,故主要建立船艏部分的模型,且采用刚体进行约束,其余部分进行等效处理。
1.1 渔船建模流程
以42 m拖网渔船为例,根据该船的型线图、型值表、基本结构图及典型横剖面图等在ANSYS APDL软件中进行建模;在HyperMesh软件中对建好的渔船模型进行网格划分、共节点处理及模型法向调整。渔船主要量度和船型系数如表1所示。
表1 渔船主尺度及船型系数
Tab.1 Main size and ship form coefficients of the fishing vessel

主尺度和船型系数main dimension and ship coefficients符号和单位symbol and unit值value总长length overallLOA/m43.20垂线间长length between perpendicularsLpp/m36.50设计水线长design waterline lengthLWL/m39.64公约船长convention masterL/m38.20型宽molded breadthB/m7.00型深molded depthD/m3.50设计吃水designed draftd/m2.80设计排水量designed displacementΔ/t503.20设计纵倾designed trimδT/m0.80肋距frame spaces/m0.50梁拱cramberf/m0.15方形系数block coefficientCb0.682 1棱形系数prismatic coefficientCp0.749 7舯剖面系数midsection coefficientCm0.909 8水线面系数waterline coefficientCw0.973 0浮心距舯the distance between buoyant center and amidshipXb-1.471
渔船建模流程如下:
1)通过型线图,读取型值表中的型值数据,建立可在ANSYS APDL软件中读取的.csv文件。
2)通过ANSYS APDL读取.csv文件,生成船体外板的关键点。
3)将每一站号的关键点进行连接,形成船体外板的基本框架。
4)由3)中生成的线,连接成面,形成船体外板。
5)根据船体基本结构图,构建甲板、横舱壁及升高甲板。
6)根据基本结构图,建立中内龙骨,并通过分割面的命令,建立强横梁、甲板纵桁和旁内龙骨等加强构件。
7)通过reflect命令,生成整船模型,检查重复点,建模完成。
1.2 商船球鼻艏有限元模型建立
在商渔船碰撞事故中,商船往往吨位较大,在碰撞过程中损伤较小,而且由于碰撞主要发生在商船的艏部和渔船的舷侧,所以可对商船模型进行简化处理。在现代商船中,球鼻艏型船艏因其独特的形状和大小,可与船行波进行相互干扰和抵消,减小船的阻力,所以该船型应用比例较高。由于本研究中主要探究渔船在碰撞中的受损情况,且球鼻艏在碰撞过程中受损情况不严重,所以可以将球鼻艏设为刚体形式,通过设置质心相对于球鼻艏的位置,对其加载,并进行一系列参数设置,使其在参数方面符合整船要求。根据前人经验[12],此简化方式对仿真结果影响不大,又可减少计算工作量及时间,故此方式可行。
为使所选商船更具代表性和典型性,经查阅资料,本研究中以韩国海洋工程研究所(Korea Research Institute of Ships and Ocean Engineering,KRISO)开发的KCS集装箱船作为撞击商船进行计算,KCS作为国际水动力学研究公认的标准模型之一,具有广泛的代表性。KCS船舶模型(以排水量5 000 t为例)主尺度和重要几何要素如表2所示。在后续计算中根据不同计算工况将撞击船按所需排水量进行缩放处理。
表2 撞击船主尺度和几何要素(以排水量5 000 t为例)
Tab.2 Main dimension and geometric element of collision ship (displacement of 5 000 t)

主尺度和几何要素main dimension and geometric element符号和单位symbol and unit值value垂线间长length between perpendicularsLpp/m104.42设计水线长design waterline lengthLWL/m105.56型宽molded breadthB/m14.62型深molded depthD/m8.63设计吃水designed draftd/m4.90设计排水量designed displacementΔ/t5 000重心垂向坐标vertical coordinates of barycenterGK/m3.31重心纵向坐标longitudinal coordinates of bary-centerGLC/m50.67
建立撞击船球鼻艏几何模型,并将其导入HyperMesh软件中进行网格划分,得到商船球鼻艏有限元模型如图1所示。
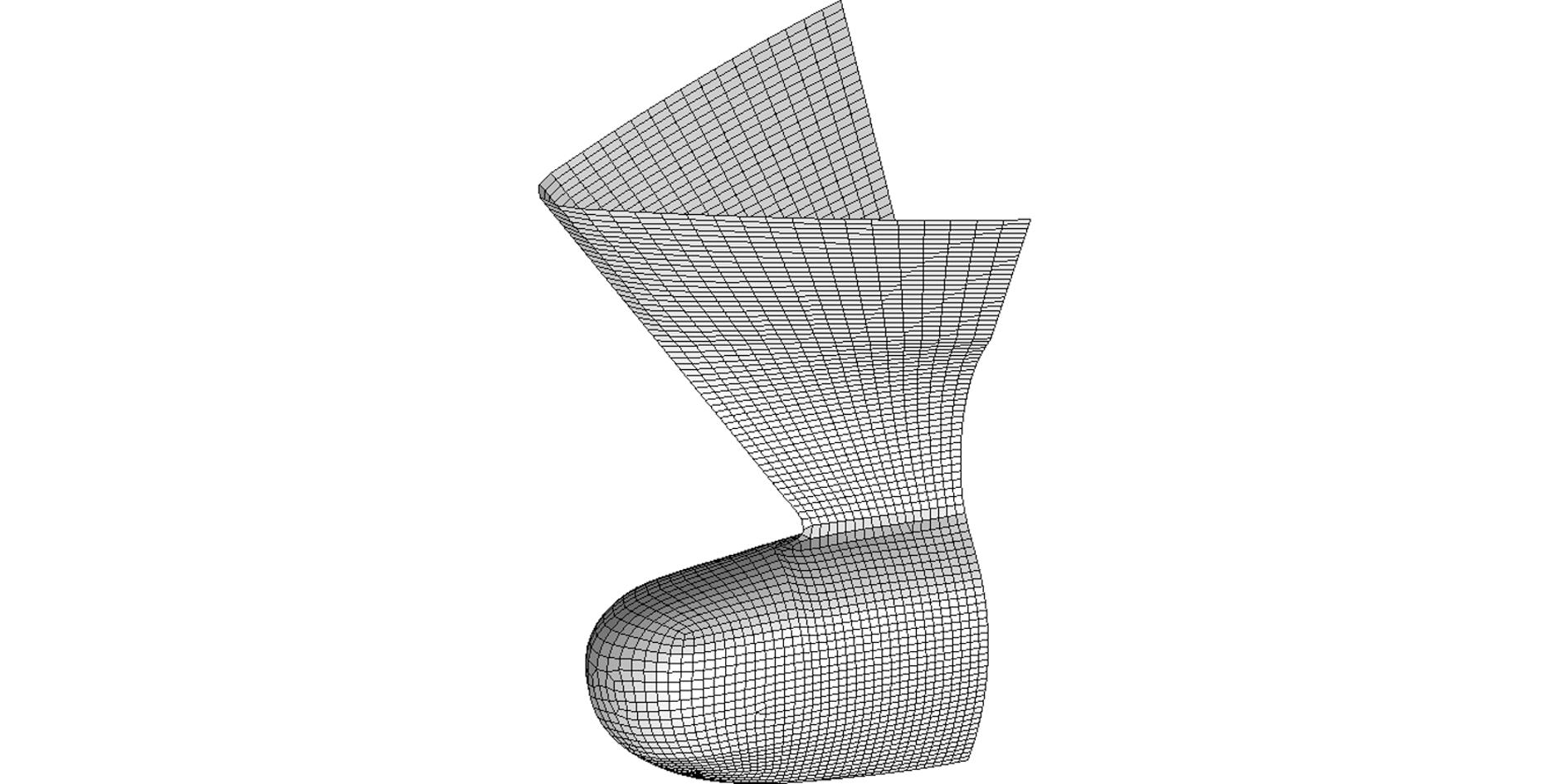
图1 商船球鼻艏有限元模型
Fig.1 Finite element model of bulbous bow of merchant ship
1.3 有限元数值模拟过程
本研究中基于有限元方法对商渔船碰撞进行模拟。除了建立商船和渔船有限元模型外,对于数值模拟过程中材料选择、边界条件施加、加载方式、接触及结构失效准则方面的设置也至关重要。
1)材料本构。船舶碰撞是一个典型的非线性动态响应过程[13],材料在受到大的冲击力作用下,大多数都会发生塑性应变[14],而碰撞区域材料变形最大,因此,该区域材料本构关系将对结果的准确性产生较大影响[15]。在未知材料拉伸特性时,可将材料的应力-应变关系简化为用带有塑性硬化的弹塑性模型表示。本研究中采用LS-DYNA软件提供的弹塑性动力学模型(*MAT_PLASTIC_KINEMATIC),该模型与温度无关,其材料本构关系[16]可由下式表示:
(1)
式中,Ep是由Ep=EtE/(E-Et)得到的塑性硬化模量。该模型中εp可以定义材料的失效。
有众多学者进行了关于应变率对屈服极限影响的研究[17],发现在较高应变率(大约为102s-1)的情况下,动屈服极限比静屈服极限(应变率是10-3s-1)高2~3倍[18]。为使材料的本构关系具有代表性和准确性,采用Cowper-Symonds本构方程[19]来描述应变率(ε)与屈服应力(σ)之间的关系,即
(2)
式中:σy为塑性应变率是![]() 时的动屈服应力;σ0为对应的静屈服应力;C和p相对于确定的材料为常数。Q235船用钢材料参数的含义及取值如表3所示。
时的动屈服应力;σ0为对应的静屈服应力;C和p相对于确定的材料为常数。Q235船用钢材料参数的含义及取值如表3所示。
表3 Q235船用结构钢材料参数
Tab.3 Material parameters of ship structural steel Q235

材料参数material parameter单位unit值value密度(ρ) density kg/m37 800弹性模量(E ) elasticity modulus Pa2.1×1011泊松比(μ ) Poisson’s ratio —0.3屈服强度(σ0) yield strength Pa2.35×108切线硬化模量(Ep ) tangent hardening modulus Pa2.50×108应变率参数(C ) strain rate parameter —40.4应变率参数(p ) strain rate parameter —5断裂应变(εf ) fracture strain —0.28
2)边界条件。为了合理模拟海上船舶碰撞场景,撞击船应设置一定的初始速度,根据碰撞工况不同还应改变商船的撞击角度、装载情况等;而被撞船设为初始静止,自由状态,不设置约束。
3)加载方式。对撞击船及被撞船的模型均进行简化处理,为了合理还原实际船舶的吨位,对被撞船加载非结构质量,质量点取在船体重心处,此外还需对被撞船设置附加水质量。采用Morora提出的经验公式[20],船舶横向运动的附加质量myy=0.4m~1.3m,其中,m为船舶总质量。
本研究中采用质量点(*ELEMENT_MASS_NODE_SET)的形式[21]将附加质量施加在水线以下船体外板上,取被撞渔船的横漂附加水质量myy=0.4m,撞击船的纵向附加质量mxx=0.04m。
4)接触算法。采用罚函数方法[22],在操作过程中注意主面和从面的选择[23],通常刚度大的面作为主面,刚度小的面作为从面,且从面网格应比主面密集。但实际上,LS-DYNA软件中最新的接触算法,即关键字中涉及“AUTOMATIC”,对主从面的选择并不敏感。例如面面接触,LS-DYNA软件自动将主从面转换为主面段和从节点,与此同时,对调主从面,即原主面转化为从节点,原从面转化为主面段,两者共同进行计算(图2)。

图2 LS-DYNA软件中的“two-way”接触算法
Fig.2 “two-way” contact algorithm in LS-DYNA
有限元模型的精准程度对计算结果有很大的影响,所以在模型建立完毕之后,应对模型进行详细检查。在提交计算之前也应对模型是否有重复点、线、面、单元,以及模型属性、模型材料、工况设置等进行检查,以提高计算效率及仿真结果的准确性,并减少计算中可能出现的问题。
5)失效准则。碰撞过程是一个瞬时过程,结构材料的应力应变会迅速经过弹性阶段,进入塑性阶段,当塑性变形达到一定值后,材料便会断裂失效。本研究中取材料的最大失效应变为0.1。该软件将通过以下准则作为判断材料失效的依据:在每一个时间步之后,如果得到单元的等效塑性应变大于单元的最大失效应变,则单元失效,在后续的计算中,失效的单元不再参与接下来的计算。
1.4 网格收敛性分析
在有限元仿真中,模型误差和计算误差是结果误差的主要来源。模型误差包括离散误差、单元形状误差和边界条件误差[24] 。
在进行有限元仿真计算中,一般而言,有限元模型具有的网格数量越多,数值仿真的结果便越准确,误差也会逐渐减小直至收敛。因此,长期以来,仿真工作者通常通过增加网格数量来提高结果的准确度。然而,随着网格数量增加到一定程度,结果的准确性不会再有明显变化,而计算成本大幅提高。因此,对网格收敛性进行验证,对于在满足精度的要求下较少地消耗计算资源有极大的帮助。
在典型船舶碰撞方面,前期的网格收敛性分析研究较少,本研究中根据被撞渔船总长为43.2 m,对其分别生成边长为0.20、0.15、0.10、0.05 m的网格,在不同网格尺寸计算中,撞击船参数不变,均为钢制球鼻艏,速度为6 m/s,初始角度为90°,撞击渔船非舱壁的位置。商船质量为5 000 t,满载,垂直撞向不同网格尺寸渔船的工况下,计算碰撞后渔船的等效应力、应变云图。
从图3、图4可见:当渔船网格尺寸为0.20、0.15 m时,渔船破损不明显,相同工况下,渔船破损情况与网格尺寸为0.10、0.05 m的情况下相差较大,不能准确反映渔船破损情况;当渔船网格尺寸为0.10、0.05 m时,渔船有明显的破口,且渔船破口形状和大小基本相似。

图3 不同网格边长下渔船等效应力云图
Fig.3 Equivalent stress cloud maps of fishing vessel at different mesh lengths

图4 不同网格边长下渔船应变云图
Fig.4 Equivalent strain cloud maps of fishing vessel at different mesh lengths
表4展示了不同网格尺寸下模型的网格数量和计算时间,随着网格尺寸的减小,模型网格数量呈指数式增长,计算时间也有同样的增加趋势。结合不同网格尺寸下渔船的应力、应变云图(图3、图4)可知,网格尺寸分别为0.10、0.05 m时,渔船破损情况基本一致,而网格尺寸为0.10 m时,计算时间远小于网格尺寸为0.05 m时。因此,选择网格尺寸为0.10 m,既可以比较准确地反映渔船破损情况,又可大幅减少计算时间。
表4 不同网格边长下模型网格数量及计算时间
Tab.4 Number of model meshes and calculation time under different mesh length
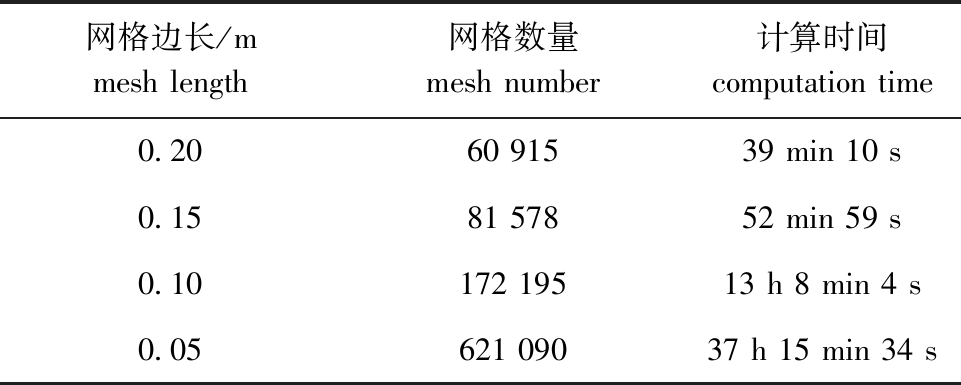
网格边长/mmesh length网格数量mesh number计算时间computation time0.2060 91539 min 10 s0.1581 57852 min 59 s0.10172 19513 h 8 min 4 s0.05621 09037 h 15 min 34 s
2 结果与分析
2.1 不同碰撞速度下渔船结构的损伤
对于同一艘商船而言,在不同速度下其拥有的动能不同,碰撞结果也不同。本研究中,设置渔船为静止状态,商船排水量为5 000 t,满载状态,模拟商船分别以2、4、6、8 m/s的速度用船艏垂直撞向渔船舷侧舱段中部。
从图5~图7可见,在商船撞击0.2 s时,此时渔船所受应力较小,舷侧无破口产生,但随着撞击时间延长,渔船舷侧出现破口。由渔船应力、应变云图可以看出,船体碰撞主要影响碰撞局部的区域,对远离碰撞区域的船体影响不大。破口主要为球鼻艏在舷侧的撞击部位出现,应力则以撞击部位最大,沿撞击部位向四周逐渐减小;应力在短时间内便达到峰值,渔船产生破口,随后破口增大,应力也随即传播到船舷并向艏艉两端扩散。从撞击0.8 s往后,应力、应变云图基本维持不变,渔船所受最大应力不再增加,渔船破口大小也不再变化,渔船破损情况不再继续恶化。由此可得,在撞击0.8 s之后,渔船与商船在破损位置的速度趋于一致,渔船在商船的带动下发生运动。通过仿真结果动态展示也可看出,渔船初始状态静止,在商船撞上渔船后,渔船局部发生变形,应力由碰撞区域向四周传递,并在短时间内到达峰值,渔船破口随碰撞时间在碰撞区域先增大,随着商船与渔船接触时间延长,渔船逐渐与商船共速,渔船破口不再增加,基本维持稳定。而渔船此后产生了与商船同向的水平运动,以及绕商船球鼻艏的旋转运动。从图5和图7可见,在碰撞发生时,船体骨架先受到较大的应力,表示船体骨架在碰撞过程中承受了大的应力[25],对船体强度有较大的贡献作用。通过对比可以看出,船体骨架的断裂变形晚于船体外壳破损,表示船体骨架在碰撞过程中对船体结构有较强的支撑作用。

图5 不同碰撞速度下渔船等效应力云图(θ=90°,Δ=5 000 t)
Fig.5 Equivalent stress cloud maps of fishing vessel at different collision speeds(θ=90°,Δ=5 000 t)

图6 不同碰撞速度下渔船等效应变云图(θ=90°,Δ=5 000 t)
Fig.6 Equivalent strain cloud maps of fishing vessel at different collision speeds(θ=90°,Δ=5 000 t)

图7 不同碰撞速度下渔船船体骨架等效应力云图(θ=90°,Δ=5 000 t)
Fig.7 Equivalent stress cloud maps of fishing vessel’ skeleton at different collision speeds(θ=90°,Δ=5 000 t)
从图8可见,随着商船碰撞速度的增加,碰撞力卸载次数同时增加。由于速度增加,碰撞力峰值发生的时间略有前移,第一次碰撞力峰值发生在撞击0.3 s左右。当商船碰撞速度为2、4 m/s时,渔船未发生破损,碰撞力未出现卸载情况;而当碰撞速度为6、8 m/s时,渔船破损,船体骨架断裂,碰撞力多次卸载,撞击速度越大,卸载后碰撞力也越大。随着商船速度增加,撞击时的动能增大,撞击过程也愈加剧烈,船体变形增大,内部结构的破坏程度也增加。由此可见,速度对碰撞力的影响较大,但碰撞力第一次峰值出现的时间与撞击速度的大小关系不大。
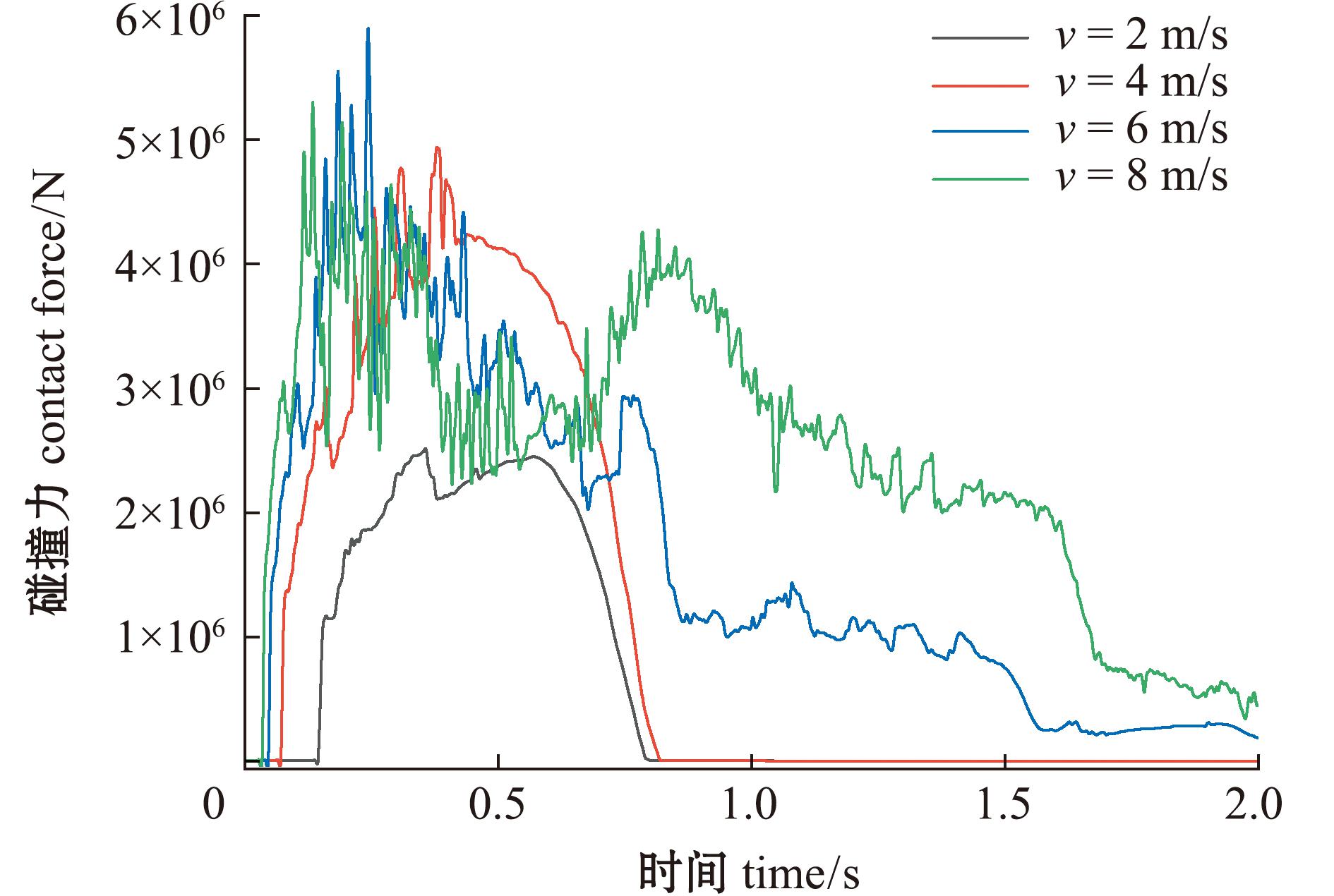
图8 不同碰撞速度下碰撞力变化曲线
Fig.8 Collision force curves at different collision speeds
从图9可见,由于渔船处于静止状态,无约束,所以在碰撞发生后,渔船主要会有两部分的变化,首先是渔船结构的破坏,其次是渔船的运动。商船碰撞渔船的动能同时转化成渔船的内能和商船的动能。通过能量变化曲线对比可知,总体趋势来看,两种能量都处于先上升后稳定状态。在碰撞初始,内能增加速度明显大于动能,这是因为此时接触时间短,由于惯性作用,渔船不能在一开始就被商船带动,此时渔船内能增加更多,商船能量大多转化为渔船的内能。这是渔船破损的原因,也是初始内能变化速度大于动能变化速度的原因。后期动能增加速度大于内能,这是由于在碰撞过程中,渔船船体破损并发生移动,渔船速度增加,动能增加,商船速度减小,两船相对速度也减小,船体破损程度减小。
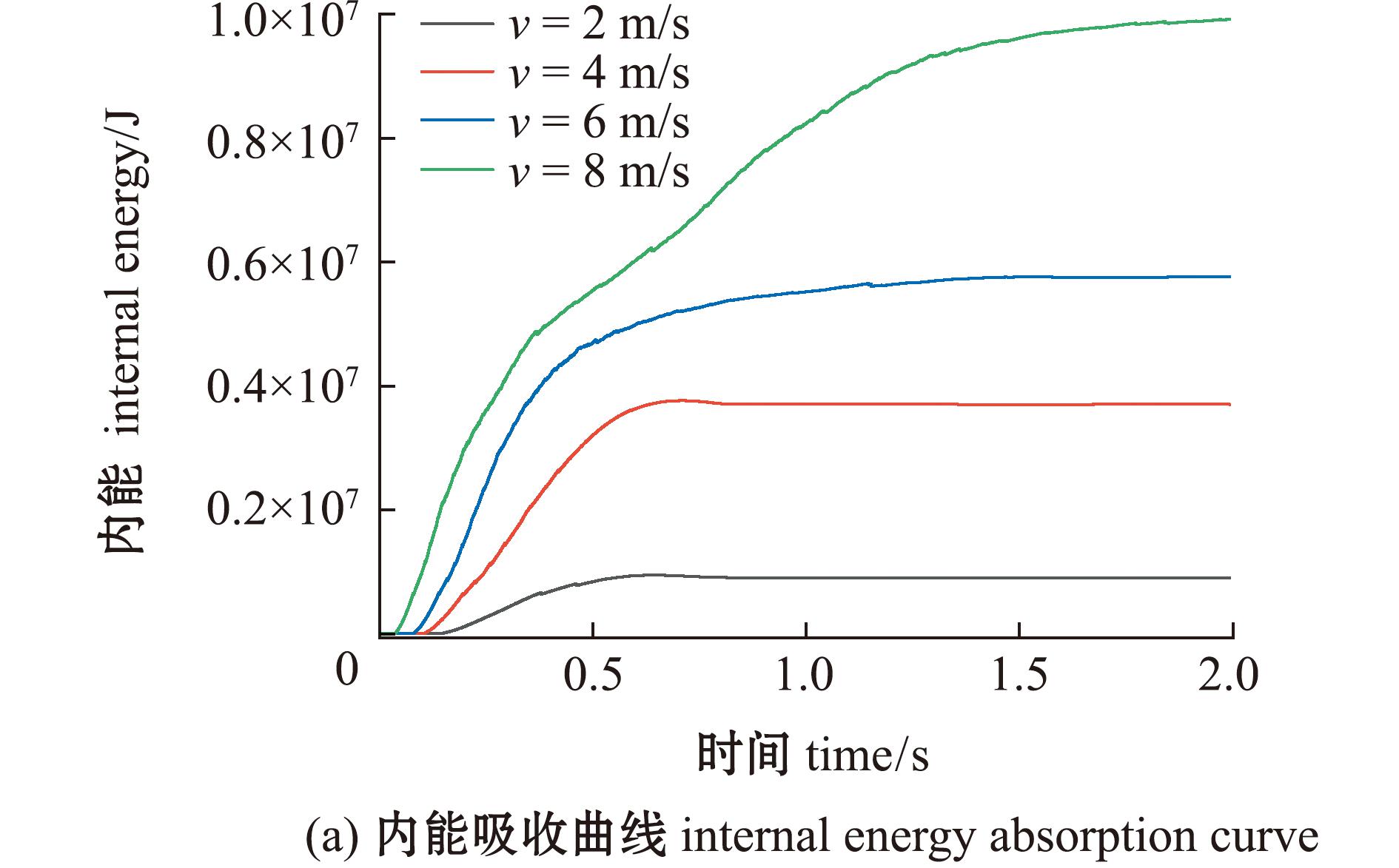
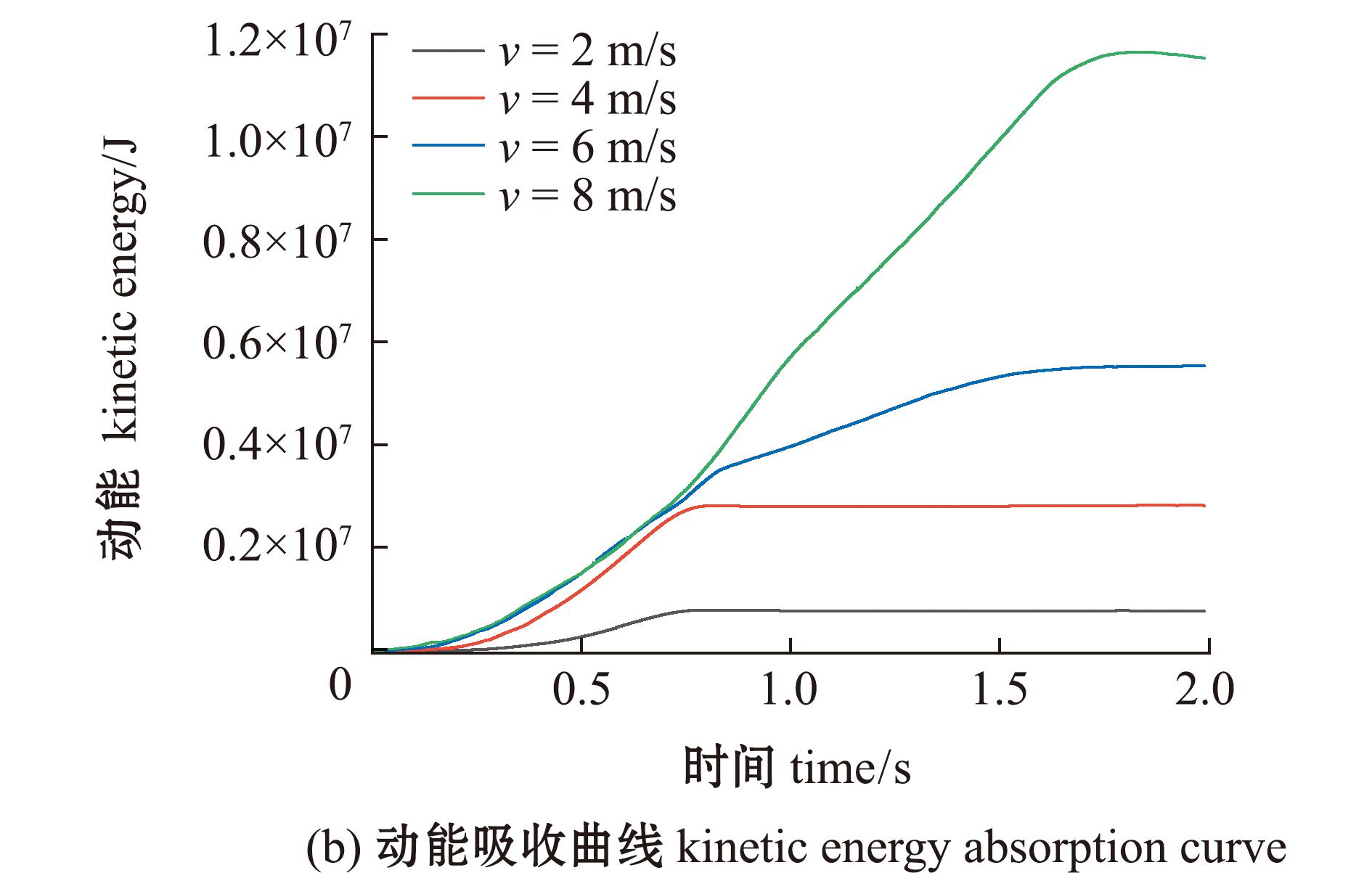
图9 不同碰撞速度下能量吸收曲线
Fig.9 Energy absorption curves at different collision speeds
2.2 不同碰撞角度下渔船结构的损伤
在实际航行中,并不是所有商船都是垂直撞向渔船舷侧位置,与渔船有一定角度的碰撞也时常发生。在商船以不同角度撞向渔船时,商船对渔船的速度可以分解为垂直于渔船方向和沿渔船船长方向。垂直于渔船方向的速度,对渔船产生直接的撞击破坏,而沿渔船船长方向的速度会使渔船相对于球鼻艏发生运动,造成损伤。本研究中,设置撞击角度分别为30°、60°、90°的碰撞工况,商船初速度为6 m/s,商船排水量5 000 t,满载状态。渔船初始仍处于静止状态,不施加约束。
从图10~图12可见:当商船以30°的初始碰撞角度撞向渔船时,只使渔船舷侧产生小变形,并未产生破口;当碰撞角度分别为60°、90°时,碰撞情况较为严重,渔船均出现大的破口,骨架也发生断裂,且60°时的破口大于90°。这表明,商船以一定角度撞向渔船时,渔船破口大小有随碰撞角度的增加呈先增大后减小的趋势。渔船产生的破口形状均与球鼻艏撞入渔船的部分形状一致,且不论碰撞角度如何,由于船体骨架连接部分易产生应力集中,往往最先达到强度极限,即渔船均有沿肋骨方向破损的趋势。由此可见,渔船破损与碰撞物体形状及渔船自身结构均有较大关系。

图10 不同碰撞角度下渔船等效应力云图(v=6 m/s,Δ=5 000 t)
Fig.10 Equivalent stress cloud maps of fishing vessel at different collision angles(v=6 m/s,Δ=5 000 t)

图11 不同碰撞角度下渔船等效应变云图(v=6 m/s,Δ=5 000 t)
Fig.11 Equivalent strain cloud maps of fishing vessel at different collision angles(v=6 m/s,Δ=5 000 t)

图12 不同碰撞角度下渔船船体骨架等效应力云图(v=6 m/s,Δ=5 000 t)
Fig.12 Equivalent stress cloud maps of fishing vessel’ skeleton at different collision angles(v=6 m/s,Δ=5 000 t)
从图13可见,初始撞击角度越大,渔船受到的撞击力越大,其中,除30°工况下撞击力大约在0.45 s时达到峰值以外,60°、90°工况下的撞击力均在0.25 s内达到峰值,并且在碰撞过程中,碰撞力出现了多次卸载现象。

图13 不同碰撞角度下碰撞力变化曲线
Fig.13 Collision force curves at different collision angles
从图14可见,在初始碰撞角度60°工况下,渔船吸收的内能和动能均最大。吸收内能最多,表示此工况下渔船的破损最严重。此图线再次证明,渔船破损严重程度并不是随着商船与其碰撞角度增加而增加,而是呈先增加后减小的趋势。
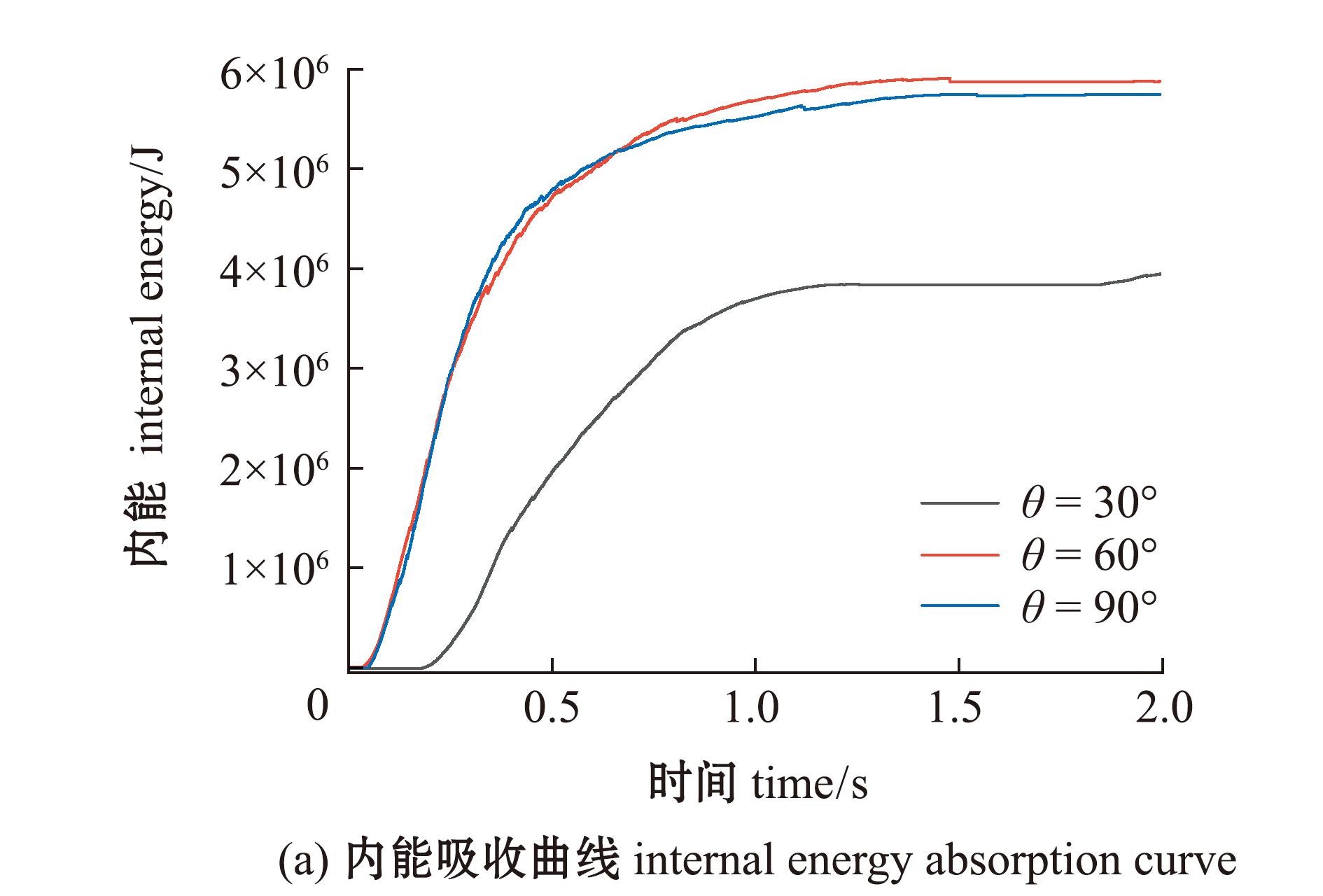
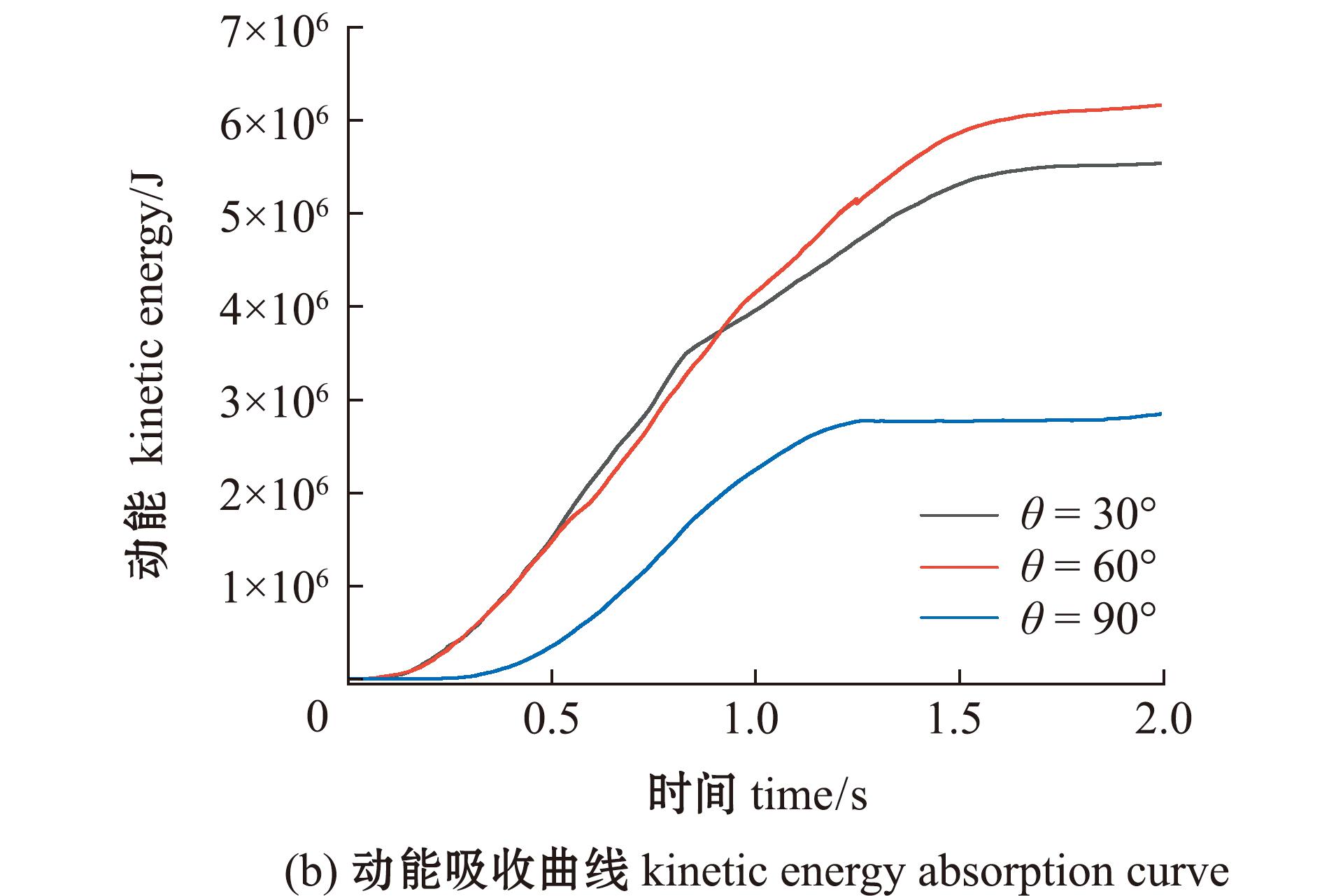
图14 不同碰撞角度下能量吸收曲线
Fig.14 Energy absorption curves at different collision angles
2.3 不同质量商船碰撞时渔船结构的损伤
船舶碰撞过程中,船的速度和质量都是船体所拥有能量的主要因素,碰撞质量越大,速度越快,商船拥有的动能越大,碰撞产生的影响也就越大。为了便于对比分析,仍计算球鼻艏初始速度为6 m/s、碰撞角度为90°且处于压载状态下撞击渔船产生的结果。通过改变刚性球鼻艏的密度,使球鼻艏的质量分别达到5 000、10 000、20 000 t来进行仿真模拟。
从图15~图17可见,随着商船质量的增加,渔船损伤越来越严重,但在商船质量为10 000、20 000 t工况下,渔船破口大小相差不大。说明商船质量达到一定程度后,质量增加对渔船破坏的影响不再十分明显。

图15 不同质量商船碰撞下渔船等效应力云图(v=6 m/s,θ=90°)
Fig.15 Equivalent stress cloud maps of fishing vessel in collision with merchant ship of different qualities (v=6 m/s, θ=90°)

图16 不同质量商船碰撞下渔船等效应变云图(v=6 m/s,θ=90°)
Fig.16 Equivalent strain cloud maps of fishing vessel in collision with merchant ship of different qualities (v=6 m/s, θ=90°)

图17 不同质量商船碰撞下渔船船体骨架等效应力云图(v=6 m/s,θ=90°)
Fig.17 Equivalent stress cloud maps of fishing vessel’ skeleton in collision with merchant ship of different qualities(v=6 m/s,θ=90°)
2.4 碰撞不同位置时渔船结构的损伤
船舶碰撞中撞击船处于不同的装载状态,如满载、压载状态,船舶吃水不同,商船球鼻艏与渔船舷侧的接触位置也不同,对渔船造成的损伤也会有一定差异。另外,在球鼻艏撞击舷侧舱壁位置或舱段中间时,由于舱壁的支撑作用,渔船碰撞损伤结果也会有所不同。因此,碰撞位置对于碰撞结果也会有重要的影响。本试验中,分别研究了商船处于满载和压载状态,不同吃水情况下对渔船的撞击特性,以及商船撞击渔船舱壁处和舱段中间无舱壁位置对渔船的撞击特性。商船均设置以6 m/s的初速度垂直撞向渔船。
从图18、图19可见:在其他条件相同的情况下,当商船处于满载状态时,对渔船的碰撞位置偏下,可对渔船造成较大的损伤,渔船会产生破口;当商船处于压载状态时,碰撞位置偏上,商船对渔船的舷墙造成了较大伤害,使舷墙发生了较大变形,但并未产生破口。因此,在其他条件相同的情况下,商船处于满载状态时碰撞位置靠下,对渔船造成的损伤大于商船处于压载状态时。

图18 满载商船碰撞下渔船等效应力、应变及船体骨架等效应力云图(v=6 m/s,θ=90°)
Fig.18 Equivalent stress-strain cloud image of equivalent stress,strain,and hull skeleton effect forces of fishing vessel in collision with merchant ship of full load(v=6 m/s,θ=90°)

图19 压载商船碰撞下渔船等效应力、应变及船体骨架等效应力云图(v=6 m/s,θ=90°)
Fig.19 Equivalent stress-strain cloud image of equivalent stress,strain,and hull skeleton effect forces of fishing vessel in collision during merchant ship of ballast collision(v=6 m/s,θ=90°)
从图20、图21可见:在其他条件保持一致的情况下,当商船撞击渔船舱段中间时,对渔船造成的损伤更严重,舱段部分船体外壳产生了破口;当商船撞击渔船舱壁处,渔船只发生了较大的形变,未产生破口。由此可见,舱壁对渔船结构强度有一定的加强作用,可承受商船对渔船的撞击力,减少碰撞过程中商船对渔船的损伤。

图20 商船撞击渔船舱段中间时渔船等效应力、应变及船体骨架等效应力云图(v=6 m/s,θ=90°)
Fig.20 Equivalent stress-strain cloud image of equivalent stress,strain,and hull skeleton effect forces of fishing vessel when a merchant ship collides at middle section of fishing vessel(v=6 m/s,θ=90°)

图21 商船撞击渔船舱壁时渔船等效应力、应变及船体骨架等效应力云图(v=6 m/s,θ=90°)
Fig.21 Equivalent stress-strain cloud image of equivalent stress,strain,and hull skeleton effect forces of fishing vessel when a merchant ship collides with bulkhead of fishing vessel(v=6 m/s,θ=90°)
3 讨论
3.1 碰撞速度对渔船损伤的影响
在商渔船碰撞事故中,碰撞速度大小是判断渔船结构损伤严重程度的关键条件。本研究中数值模拟计算结果显示,碰撞速度与渔船结构损伤严重程度成正比。这是由于商船速度增加时,动能也不断增加,碰撞力卸载次数更多,船体结构失效更多。同时,商船对渔船碰撞的时间持续得更久,碰撞力则不会很快归于零,渔船破损程度也会不断增加。该结果与赵晓博[21]的研究结果相同。因此,如果商船航行速度过快,超过安全航速,则会导致商船无法及时采取有效避碰手段,造成的渔船结构损伤也会比较严重。建议对不同质量商船制定统一的安全航速,可从源头降低碰撞事故的发生,同时也可减轻碰撞事故中渔船结构的损伤,降低人员伤亡。
3.2 碰撞角度对渔船损伤的影响
商渔船碰撞角度不同,对渔船结构造成损伤的严重程度则不同,船体的破口形状也不同,这对判定事故责任有很大的帮助。本研究中数值模拟计算结果显示,随着碰撞角度的增加,碰撞力也在不断增加,这与侯建[26]的研究结果相同,但渔船舷侧的破口在商船碰撞角度为60°时最大。这是因为碰撞时垂直于渔船方向的速度对渔船造成直接的冲击,使渔船结构发生破坏变形,而沿着渔船船长方向的速度也会使渔船因垂向速度产生的破口发生撕裂,导致破口变大。当初始碰撞角度为30°时,渔船受到的垂向碰撞力小,不足以使渔船发生破口,沿船长方向的分速度会导致渔船舷侧擦伤,也不会使渔船产生破口。当碰撞角度为90°时,渔船只受到垂直于船长方向的作用力,使渔船产生破口,并使渔船发生沿船长方向的运动。但由于渔船没有沿船长方向的速度,因此,渔船所产生的破口全部来自商船垂向速度带来的撞击,并不会因为船长方向的速度,导致破口进一步增大。当碰撞角度为60°时,渔船不仅受到垂向速度带来的撞击,同时也受到沿船长方向的速度带来的撞击,破口最大。
因此,当商船在无法避免与渔船发生碰撞时,可以通过应急操舵等操作改变相撞船舶的碰撞态势。同时,在实际场景中若发生碰撞事故且遇到肇事船舶逃逸现象,可通过鉴定渔船的受损程度,根据破口形状和位置,使其与试验结果进行对比,合理还原事故发生时逃逸船舶的航行状态,结合商船的航行记录可以推断当事船舶是否采取了有效的避让措施,为判定事故责任提供理论支持,为受害渔船索赔提供合理依据。
4 结论
1)船体骨架形式对船舶破损程度有较大影响。渔船碰撞损伤主要发生在碰撞局部区域,远离碰撞区域的部位受碰撞影响较小,且损伤后破口形状与撞击船的船艏形状有关。因此,适当增加渔船船壳厚度,对船体骨架进行合理规划,以及对船体舷侧进行局部加强,可减少碰撞过程中渔船产生的损伤。
2)碰撞发生时,商船速度越大,碰撞吸收的能量也越多,渔船受损越快且程度越严重。在本研究中设置的工况下,商船速度≤4 m/s时,撞击渔船不会对渔船造成破口。因此,应对不同质量的商船制定统一的安全航速。
3)随着碰撞角度的增加,渔船的受损程度先增加后减小。在本研究中的3个碰撞角度中,商船以60°的初始角度撞向渔船,对渔船造成的损伤最严重。
4)在商船其他条件相同时,商船质量越大,被撞渔船破损程度越大。当商船质量超过10 000 t后,商船质量增加对渔船造成损伤的影响程度变化不大。
5)商渔船发生碰撞是在极短时间内完成的,且会对渔船造成巨大的局部破坏,一旦碰撞事故发生,渔船自救的机会很小,因此,建议商船在碰撞事故无法避免时,尽量采取降低航速、变换航向等手段减小事故损伤。
[1] MINORSKY V U.An analysis of ship collision with reference to protection of nuclear power ships[J].Journal of Ship Research,1959,3(2):1-4.
[2] PETERSEN M J.Dynamics of ship collisions [J].Ocean Engineering,1982,8(4):295-329.
[3] 梁文娟.船舶碰撞的三维分析[J].上海船舶运输科学研究所学报,1986,9(1):80-93.
LIANG W J.Three-dimensional analysis of ship/ship collision[J].Journal of Shanghai Ship and Shipping Research Institute,1986,9(1):80-93.(in Chinese)
[4] MOTOR A,SEIZ O,FUJIN O,et al.10.Equivalent added mass of ships in collision[J].Selected Papers from the Journal of the Society of Naval Architects of Japan,1971,7:128-138.
[5] PEDERSEN P T,ZHANG S.Absorbed energy in ship collisions and grounding-revising Minorsky’s empirical method [J].Journal of Ship Research,2000,44(2):140-154.
[6] 刘敬喜,叶文兵,徐建勇,等.内河双壳油船舷侧结构耐撞性分析[J].中国造船,2010,51(1):219-226.
LIU J X,YE W B,XU J Y,et al.Crashworthiness analysis for inland double hull tanker side structures[J].Shipbuilding of China,2010,51(1):219-226.(in Chinese)
[7] 刘昆,洪婷婷,李江涛,等.基于全耦合分析技术的折叠式夹层板船体结构碰撞性能研究[J].船舶工程,2014,36(6):27-30,121.
LIU K,HONG T T,LI J T,et al.Research on collision performance of sandwich ship structure based on fully-coupled analysis method[J].Ship Engineering,2014,36(6):27-30,121.(in Chinese)
[8] HARIS S,AMDAHL J.Analysis of ship-ship collision damage accounting for bow and side deformation interaction[J].Marine Structures,2013,32(7):18-48.
[9] RINGSBERG J W,HOGSTRM P.A methodology for comparison and assessment of three crashworthy side-shell structures:The X-core,Y-core and corrugation panel structures[C]//Collision and grounding of ships and offshore structures-proceedings of the 6th international conference on collision and grounding of ships and offshore structures,ICCGS 2013.Trondheim,Norway:Taylor and Francis-Balkema,2013:323-330.
[10] RINGSBERG J W,AMDAHL J,CHEN B Q,et al.Marstruct benchmark study on nonlinear FE simulation of an experiment of an indenter impact with a ship side-shell structure[J].Marine Structures,2018,59:142-157.
[11] PAIK J K,PEDERSEN P T.Modelling of the internal mechanics in ship collisions[J].Ocean Engineering,1996,23(2):107-142.
[12] 王泽平.船舶斜撞场景下结构动力响应及变形机理研究[D].上海:上海交通大学,2021.
WANG Z P.Research on dynamic response and deformation mechanism of ship structures under ship oblique collisionscenario[D].Shanghai:Shanghai Jiao Tong University,2021.(in Chinese)
[13] 苏伟江.基于有限元法的渔船碰撞仿真研究[D].大连:大连海事大学,2015.
SU W J.Fishing vessel collision simulation based on finite element method[D].Dalian:Dalian Maritime University,2015.(in Chinese)
[14] 张泉乐,薛荔.非线性问题的有限元法[J].武汉理工大学学报,2010,32(15):178-180.
ZHANG Q L,XUE L.Non-linear finite element method the problem[J].Journal of Wuhan University of Technology,2010,32(15):178-180.(in Chinese)
[15] JONES N.Structural impact[M].Cambridge:Cambridge University Press,1989.
[16] 孟阿军.冲击载荷下加筋板壳结构损伤数值仿真[D].武汉:华中科技大学,2007.
MENG A J.Numerical simulation on the failure of stiffened plate and shell structure under impact of dynamic loading mechanism[D].Wuhan:Huazhong University of Science and Technology,2007.(in Chinese)
[17] ROACHE P J.Perspective:a method for uniform reporting of grid refinement studies[J].Journal of Fluids Engineering,1994,116(3):405-413.
[18] 杨冬梅.板壳结构在冲击载荷作用下的破坏机理研究[D].哈尔滨:哈尔滨工程大学,2005.
YANG D M.The destroy mechanism study of plate structure under shock load[D].Harbin:Harbin Engineering University,2005.(in Chinese)
[19] 廖其红,黄宏成,薛量.薄壁钢结构碰撞性能仿真中的材料模型研究[J].机械设计与研究,2001,17(4):64-66,9.
LIAO Q H,HUANG H C,XUE L.On material model for thin-walled sheet metal crash worthiness simulation[J].Machine Design and Research,2001,17(4):64-66,9.(in Chinese)
[20] 陶亮.船舶舷侧结构碰撞性能研究[D].大连:大连理工大学,2006.
TAO L.Research on characteristics of ship side structure in collision[D].Dalian:Dalian University of Technology,2006.(in Chinese)
[21] 赵晓博.船舶碰撞的有限元仿真研究[D].武汉:武汉理工大学,2016.
ZHAO X B.Research on finite element simulation of ship-ship collision[D].Wuhan:Wuhan University of Technology,2016.(in Chinese)
[22] 黄毅铭.船舶舷侧新型耐撞结构研究[D].镇江:江苏科技大学,2014.
HUANG Y M.Study on a new type of collision-resistant structure on the ship’s side[D].Zhenjiang:Jiangsu University of Science and Technology,2014.(in Chinese)
[23] 李磊.渔船碰撞损伤的数值仿真研究[D].舟山:浙江海洋学院,2012.
LI L.Numerical simulation of the collision damages of fishing vessels[D].Zhoushan:Zhejiang Ocean University,2012.(in Chinese)
[24] 张俊.有限元网格划分和收敛性(一)[J].CAD/CAM与制造业信息化,2010,182(4):99-103.
ZHANG J.Mesh division and convergence of finite element (I)[J].Intelligent Manufacturing,2010,182(4):99-103.(in Chinese)
[25] 解国强.Abaqus/Explicit在船舶碰撞载荷作用下结构优化中的应用[J].舰船科学技术,2021,43(12):19-21.
XIE G Q.Application of Abaqus/Explicit in ship structure optimization under collision load[J].Ship Science and Technology,2021,43(12):19-21.(in Chinese)
[26] 侯健.全船有限元强度分析及船舶碰撞仿真[D].大连:大连理工大学,2012.
HOU J.Strength analysis of overall ship FEM model and simulation of ship collision[D].Dalian:Dalian University of Technology,2012.(in Chinese)