在自然界中,大多数河道通常是由主槽和滩地等单元构成,其横断面呈复式形态。在枯水期间主要在河道主槽内泄流,洪水期间,水流溢出河道主槽漫溢至滩地,形成淹没过流。在这些滩地上,一般都生长不同层次或不同类型的植被,如矮小的草、低矮的灌木及高大的乔木等。传统的观点认为,河滩上生长的植物不仅可以减缓水流速度,减少水土流失,稳固河岸,还可起到净化水体、美化环境的生态作用,河道滩地植被是一种既经济又有效的生态治河措施[1]。然而,在洪水期,这些生长在滩地的植被在一定程度上会改变滩槽内部原有的水流流动结构,而植物和水流间的相互作用会使河道中部分水流的能量转换成了在植物附近产生的湍流动能,从而降低河道的行洪能力。因此,了解河道滩地植被对水流的扰动特性,进而分析滩地植被作用的利弊关系,其结果对于水利防洪、护堤工程及河道生态保护与修复等工作都有着重要的研究意义。
目前,河道滩地植被在堤岸的固滩、护堤及防洪中的问题受到越来越多的关注,已经成为当前研究的热点,国内外诸多学者对河岸生态护坡开展了相关研究工作。随着计算机技术和数值计算理论的发展,数值模拟技术在试验水槽、湖泊、河流、海湾及海岸等工程中得到成功的应用,应用二维和三维数学模型对局部植被作用下明渠流动的模拟研究在国内外也有较多的报道。如Su等[2]应用大涡模型模拟了植被作用下明渠水流的三维流动特性,解释了刚性植物与水流相互作用规律。Wilson等[3]通过数学模型研究了不同的柔性植物对水流流动的影响。Li等[4]使用三维大涡模拟方法计算了明渠中植物与水流的相互作用。上述学者的研究中,均在模型方程中增加植物拖曳力项来表达植物对水流的阻滞作用,其拖曳力与植物的参数有关,主要包括植物类型、密度、高度、直径、刚柔性等信息。另外,Asaeda等[5]、Benjankar等[6]、Asami等[7]分别结合数值模拟技术研究了滨岸植被河岸稳定性的力学机理,以及树木、河道形态与溃堤洪水演进之间的相互作用。Ghani等[8]运用Fluent软件分析了植被明渠水流纵向和横向流速的垂向分布特征,并给出了植物区内湍流强度的变化规律。还有一些学者针对植被与水流的交互作用也做了许多研究工作,如张明亮等[9]建立了三维曲线坐标下的k-ε双方程湍流数学模型,在动量方程和湍流方程中增加拖曳力源项来考虑植被对水流和湍流动能的影响,分析了在浅水植被作用下复式明渠内的流体运动特征。刘彦东等[10]将柔性沉水植物区域概化为多孔介质区域,采用RNG k-ε双方程湍流模型对含柔性沉水植物河道的三维水动力特性进行了数值模拟。黄本胜等[11]将珠江三角洲典型的窄滩河道概化为简单复式断面河道,通过对有无植被条件下滩地的水动力进行模拟,定性分析了滩地有无种树对窄滩复式河道水动力特性的影响。Zhao等[12]基于三维数学模型对水流在不连续的间断刚性植被区进行了模拟,进一步分析了不同密度斑块植被分布对水流流动结构的影响。对于复式河道来说,由于自身的断面特点,导致其内部流体运动比较复杂,再加上滩地植物与水流间的相互作用,使其水动力特性变得更加复杂。此外,滩地上植物的排列形式、植物密度及生长高度也是扰动复式河道水体流动的重要因素。就目前而言,滩地植被对河道行洪会产生怎样的影响,以及不同高度滩地植物对河道水动力特性的影响机制等尚不明晰,而且国内外涉及此类问题的研究主要是通过植物拖曳力将植被阻力进行简单量化,对水动力与植被交互作用的精细化模拟研究尚不多见,因此,相关研究工作亟须开展。
本研究中,基于计算流体动力学仿真软件Fluent,对含有刚性植被的复式断面明渠水流进行了数值模拟。首先通过有无植被作用下的物理模型试验数据验证了模型的准确性,进而分析了不同高度植被作用下复式河道的流场分布规律,重点研究了滩地植被对滩槽水体能量交换特性的影响机制,并对变化入流流量条件下主流流速和紊动强度沿垂线的分布规律进行了探讨,以期能精细化模拟滩地植被对复式河道水动力特性的影响,为河流防洪工程、河道浅滩整治及生态护岸等工程的实施提供科学依据。
1 数学模型
1.1 基本方程
连续方程:
(1)
动量方程:
(2)
湍流动能方程:
Gk-ρε;
(3)
耗散率方程:
(4)
其中: u、v、w为水体在x、y、z3个方向的流速;p是流体的动水压强;ρ为水体的密度;k为流体湍流动能;ε为湍流动能耗散率;Γφ为有效黏性系数;Cε1、Cε2、σk、σε为湍流常数,Cε1=1.44,Cε2=1.92,σk=1.0,σε=1.3;Gk为平均速度梯度引起的湍动能k的产生项[9]。
1.2 数值求解方法
Fluent软件具有先进的数值计算方法和强大的前后处理功能,是当前世界上最先进的流体力学仿真软件之一。Fluent软件采用有限体积法离散三维N-S方程,采用压力速度耦合方式(SIMPLE算法)求解离散的方程组。Fluent软件具有多个湍流流动模型,其中,标准k-ε湍流模型具有较高的计算精度和效率,已在不同工程算例中得到成功的应用,因此,本研究中采用标准k-ε湍流模型封闭N-S方程中的雷诺应力。此外,网格划分与生成是决定模型成功与否的重要因素之一。Fluent软件可以采用结构性网格或者非结构化网格剖分计算域,也可采用两者相融合的方式,使网格更加灵活简便。在计算过程中,当某一变量残差小于1×10-6,且所有模拟变量随时间的变化基本保持不变时,认为计算收敛,计算任务结束。
1.3 边界条件设置
本次计算模拟为带有复式断面河槽的均匀水流,其边界条件设置如下:
进口边界:上游进口给定流速、湍流动能及湍流动能耗散率。入口速度(v0)是利用平均流速来控制河道入流流量大小,其值设置为v0=0.365 m/s,湍流动能k=4.805 608×10-3 m2/s2,湍流动能耗散率ε =9.481 236×10-5 m2/s3。下游出口边界为压力出口。
固体壁面边界:计算域底边界和两侧壁边界,采用无滑移的固壁条件,并由壁面函数法处理。
水面边界:假设水面无剪切和滑移速度,当自由界面处理,压力值为标准大气压。
2 模型验证
2.1 物理模型描述
采用杨克君[13]水槽试验中的工况1和工况2作为验证算例,其中水槽长16 m、宽0.3 m、高0.4 m,坡度s=0.125%。此试验的工况1不存在植物,工况2中用弹性模量较小的塑料管来模拟滩地植被,以交错的方式种植在距槽首8.2 m~11.2 m的范围内,如图1(a)所示,B为滩槽总宽度,B1为滩地宽度,B2为主槽总宽度,L为植被区域总长度。该试验的测量断面位于距离槽首9.6 m处,在断面上选取4条垂线沿深度方向进行速度测量,每条垂线分别距滩地的壁面8、13、22、26 cm,分别位于滩地中心、滩槽交界处、主槽边坡起点及主槽中心位置[13],如图1(b)所示。本研究中主要应用Fluent软件对植被作用下流体运动的物理模型试验进行精细化模拟,进而探究滩地植被对滩槽水流的动量交换和水流阻滞的影响机制。在工况1和工况2的基础上,本研究中改变了植物高度,分别为14、4.8 cm,即增加了工况3和工况4,具体的特征参数如表1所示。


图1 复式河道示意图
Fig.1 Schematic diagram of the compound channel
表1 复式河道的特征参数与计算域网格信息
Tab.1 Parameters in the compound channel and grid information for the computed domain

工况condition床面底坡/%bottom slope of the bed流量/(L·s-1)flow rate水深(H)/mwater depth种植方式planting pattern网格信息grid information主槽main channel滩地floodplain行距/cmline spacing株距/cmrow spacing高度/cmheight直径/cmdiameter节点数node单元数element工况1 case 10.12517.720.1980.1383 001 2492 822 400工况2 case 20.12517.720.2000.140329.60.68 236 4637 486 965工况3 case 30.12517.720.2000.140324.80.65 506 01450 111 463工况4 case 40.12517.720.2000.1403214.00.610 117 4309 187 906
在数值模拟中,由于计算域的大小会直接影响模型的计算效率,为减少数值模拟的计算耗时和确保计算的准确性,本研究中的计算区域为9 m,植被区前后分别选取3 m,以及整个植被区域。应用Fluent前处理软件Meshing对4个工况的计算域进行非结构化网格划分,刚性植物被当作固体不透水边界来处理(图2)。考虑到植物区内植被分布比较复杂,其流态变化剧烈,因此,必须对植被区域进行网格加密处理,以保证获取高精度的计算结果。针对不同的计算工况划分网格,计算域的网格信息如表1所示,水平方向最小网格单元约为0.001 2 m,垂直方向最小网格单元约为0.000 46 m。

图2 计算域植被区附近的网格示意图
Fig.2 Mesh sketch near vegetation domain
2.2 水动力模型的数值结果验证
首先对工况1进行模拟分析,主要是验证Fluent软件中模型参数设置的正确性。在该算例中,其计算结果的横纵坐标分别被无量纲化,Hr=z/H为相对高度,其中z为测点距水面的距离,H为水深,则河床底部相对高度为0,水面相对高度为1;u/v0为相对速度,其中u为水流速度,v0为入口流速。图3给出了工况1的不同测点主流速度计算值和实测值的对比结果,由图3可知,数值模拟结果与测量值符合较好,4个测点主流速度的垂向分布基本呈现对数分布。由于水槽底部存在摩擦阻力,使水槽底部的主流速度较小,随着相对高度的增大,主流速度在垂向上也逐渐增大。图4为工况2各测点主流速度沿水深方向的计算值和实测值的对比结果,当滩地有植物作用时,测点1主流速度的垂向分布不再服从对数分布,在植被区的流速变化幅度很小,在植物和水流的过渡层区域,存在较大的速度梯度,主要原因是植被冠层的阻力影响,在植被冠层以上区域的速度呈现出对数分布规律。测点2(d=13 cm)位于滩槽交界处,速度计算值和实测值略有差距,主要原因是模型未考虑植物在水流作用下的变形,同时滩槽交界区的流态复杂,其二次流对植物的横向变形也产生了一定影响[9]。由于测点3和4(d=22、26 cm)远离植物区,其主流速度沿深度方向符合对数分布规律。
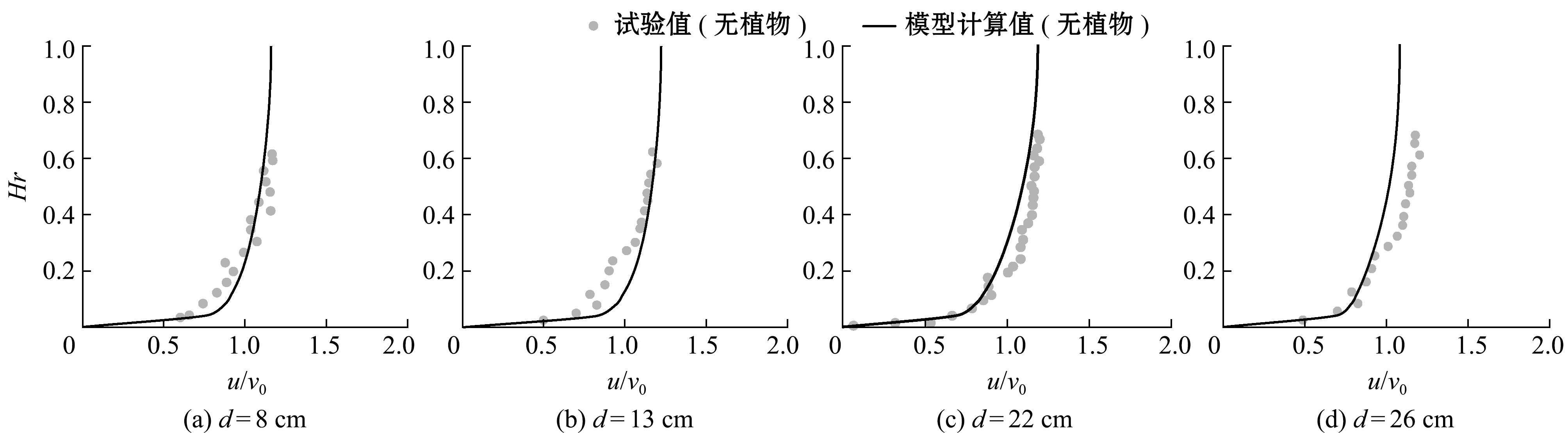
图3 工况1条件下主流速度模型计算值和实测值的对比验证
Fig.3 Comparison and validation of the calculated and measured velocities of main stream in case 1 condition
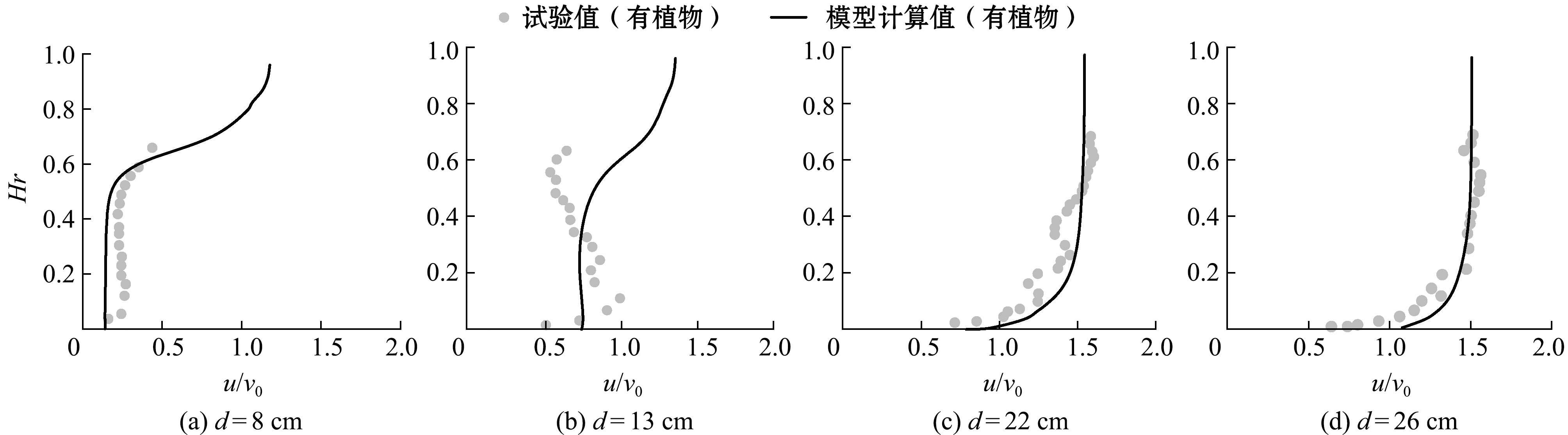
图4 工况2条件下主流速度模型计算值和实测值的对比验证
Fig.4 Comparison and validation of the calculated and measured velocities of main stream in case 2 condition
图5为有无植被工况(工况1、工况2)模拟的主流流速等值线图,当河道滩地内无植物存在时,断面速度的分布比较均匀,说明在此水深条件下,滩地流量分配比较大,能够承担复式断面河道的过流流量;当滩地种植植物后,由于植物的阻碍作用其水体流速明显减小,在植物域内存在明显的低流速区,主流转移到河道主槽内。由此可见,滩地存在植物将导致其过流能力减弱,这种作用将直接影响洪峰期河道的行洪效果。
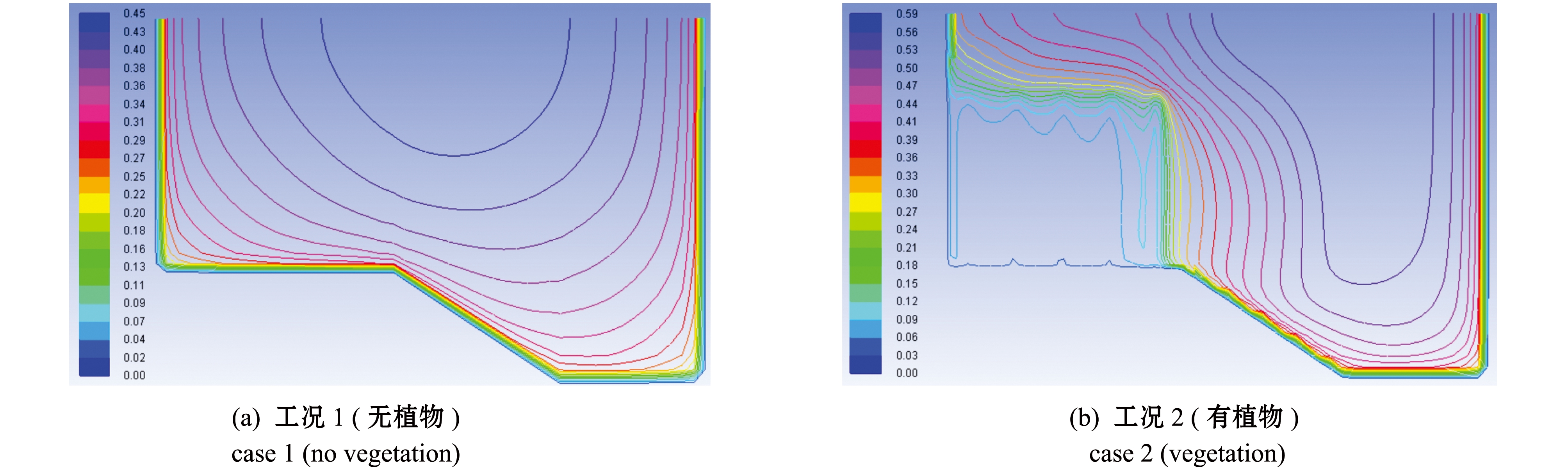
图5 有无植被条件下模拟的横断面流速等值线图
Fig.5 Simulated velocity contour plots in the absence and presence of vegetation
2.3 植物高度变化对水动力特性的影响
为了研究滩地植物高度对复式断面明渠水动力特性的影响,在水深恒定条件下,构建了滩地长有不同高度植物的模拟场景(表1中工况2、工况3、工况4),其相对应的植物高度分别为9.6、4.8、14.0 cm。由于滩地上的水深为14 cm,因此,植物高度4.8、9.6 cm工况为淹没状态,而植物高度14.0 cm工况为非淹没状态。图6给出了不同植物高度条件下各测点主流速度的对比结果,针对淹没工况,植物高度的变化对滩地中心位置的主流速度影响较大,尤其是在植物顶部处速度的变化最为显著(图6(a));在非淹没工况,水体主流速度沿水深方向几乎无变化。在滩槽交界处,受滩地植被高度的影响,其主流速度变化较大(图6(b))。在主槽区,尽管滩地植物的高度不同,但其主流速度垂向分布大体一致,由于主槽底部存在摩擦力,水体靠近主槽底部的流速较小,随着相对高度增加,主流速度逐渐增大,到达水面时的速度为最大(图6(c)、(d))。此外,由图6还可以看出,滩地植物的存在对滩地区和主槽区的主流速度影响较大,滩地植物越高,滩地植物区流速越小,而主槽区的主流速度则越大。

图6 不同测量位置主流速度的对比验证(滩地种植不同高度植物)
Fig.6 Comparison of main stream velocity in different positions (under the conditions of different height floodplain plant)
图7为工况1条件下不同测量位置的湍流动能计算值对比结果,4个测点的湍流动能最大值均出现在近水槽底部的边界层内,其最大值在0.000 9~0.001 2 m2/s2。随着相对高度的增大,湍流动能逐渐减弱,接近水面湍流动能趋于平缓,这与杨纪伟等[14]的相关研究结果一致。

图7 不同测量位置模拟湍流动能的对比(工况1)
Fig.7 Comparison of the simulated turbulent kinetic energy in different positions(case 1)
图8为不同植物高度条件下计算的湍流动能垂向分布曲线,由图8(a)、(b)可知,在滩地中心和滩槽交界处,淹没状态(4.8、9.6 cm)的植被工况计算的湍流动能曲线呈“>”型,并在植物冠层顶部位置附近湍流动能出现峰值,随着相对高度增大,植被冠层对水流的干扰逐渐减弱;非淹没状态(14.0 cm)植被工况计算的湍流动能幅值变化不大。由图8(c)、(d)分析可知,在主槽区与主槽边坡起点位置的测点,在不同高度植被作用下其湍流动能的峰值出现在水槽底部附近,相对高度大致相同,且发展趋势基本一致。
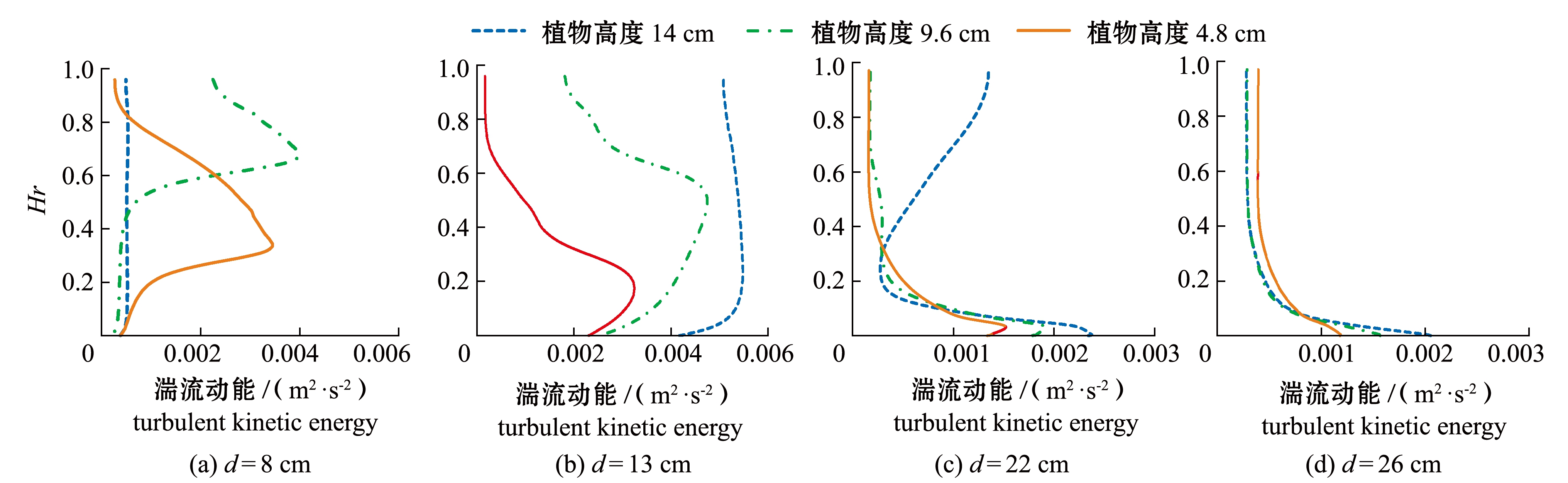
图8 不同测量位置湍流动能的对比(滩地种植不同高度植物)
Fig.8 Comparison of turbulent kinetic energy in different positions(under the conditions of different height floodplain plant)
图9为工况2条件下计算的断面二次流场矢量图,通过分析发现,由于刚性植被的阻力作用,在植被区附近形成较大的横向速度,此为形成断面二次流态强烈的扰动源,并向周围扩散,二次流会向主槽方向移动,形成顺时针方向的二次流环流。

图9 滩地植物作用下的断面二次流场矢量图(工况2)
Fig.9 Secondary flow vector diagram in the presence of floodplain plant(case 2)
图10为工况2条件下计算的水平速度矢量图(相对高度Hr=0.3),由图10可知,植株前流场变化相对平缓,在两个单株植物带间,流速变大,在植株后存在流速低速区。

图10 植物带的水平速度矢量图(工况2,Hr=0.3)
Fig.10 Velocity vector diagram near plant belt in horizontal direction(case 2,Hr=0.3)
2.4 入流流量变化对水动力特性的影响
为了研究入流流量变化对植被区及主槽区的主流流速及湍流动能的影响,本研究中针对工况2设计了3种入流流量边界条件,流量分别为10.95、17.72、22.21 L/s。从图11可见,在水深一定的情况下,入流流量越大,4个测点相应的主流速度也越大。
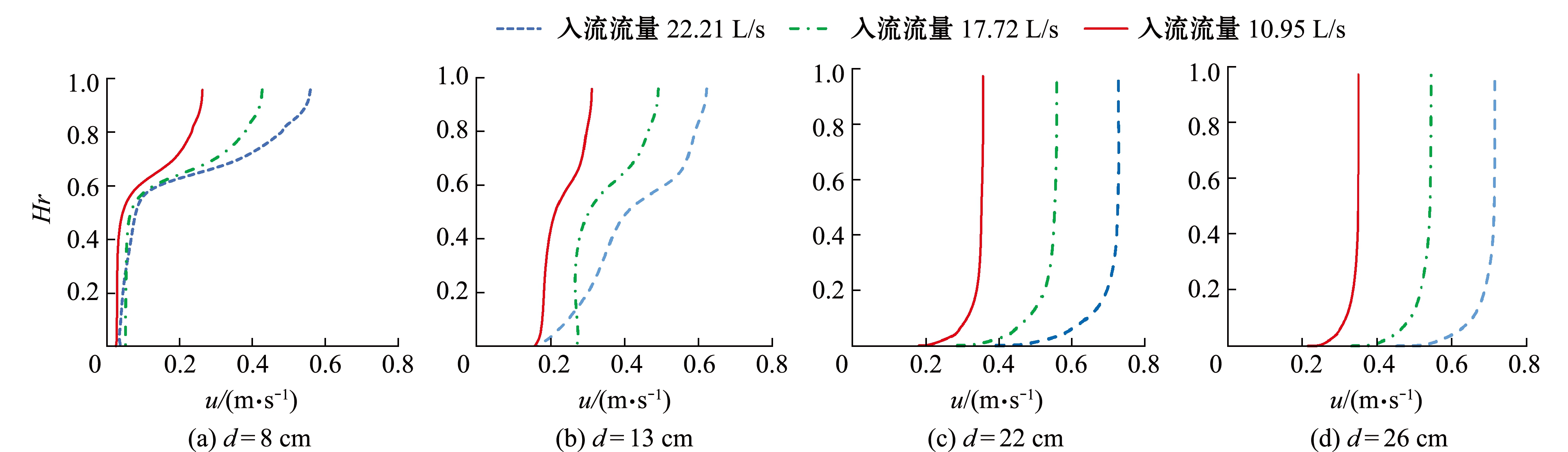
图11 不同入流流量条件下主流速度的对比(工况2)
Fig.11 Comparison of the simulated main stream velocity with varied inflow conditions (case 2)
从图12(a)可见,植物冠层顶部是分界点,冠层顶部以下区域计算的湍流动能随入流流量变化不明显,在植被冠层以上区域,随着入流流量的增加,计算的湍流动能幅值增大,变化趋势呈先增大后减小。从图12(b)可见,位于滩槽交界处区域,随着入流流量增加,计算的湍流动能值相应增加,总体变化趋势一致。从图12(c)、(d)可见,位于主槽内区域,入流流量和湍流动能呈现明显的正相关,变化趋势达到最大值后,随着相对高度的增大逐渐减小并趋于平稳。
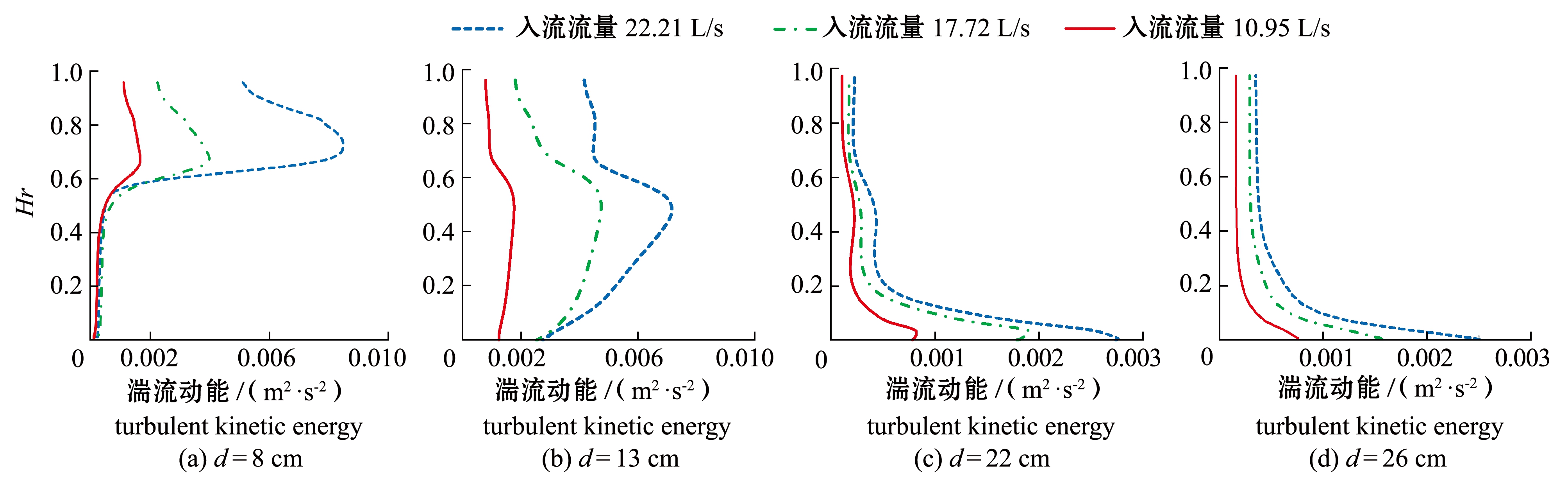
图12 不同入流流量条件下模拟湍流动能的对比(工况2)
Fig.12 Comparison of the simulated turbulence energy with varied inflow conditions (case 2)
3 结论
本研究中基于Fluent流体力学仿真软件对存在刚性植物复式断面水槽的三维流场进行了精细化的数值模拟,重点讨论了滩地植被对复式断面水槽水动力特性的影响。通过对比结果可以看出,计算值和试验测量值符合较好,说明Fluent模型能够准确地复演复式水槽的流动特征。通过对模拟结果的分析得出如下结论:
1)复式断面河道的滩地植物会改变流场的分布,使主流转向主槽,随着滩地植被高度的增加,滩地植物区主流流速相应降低,而主槽内主流流速增大趋势明显,滩地植物区的湍流动能也随植物高度增加而发生明显变化。
2)由于滩地植物的存在,使滩地植物区内产生较大的横向速度,促使复式断面产生较强的顺时针二次流。
3)当水深保持不变时,随着入流流量的增大,断面主流流速相应增大,植物区内部的湍流动能变化不大,但在植物冠层顶端的湍流动能明显变大,冠层顶端其他测量位置湍流动能趋势相同,幅值随流量增加而变大。
实际情况中,针对具有复式断面结构的天然河道,滩地植被的存在使其紊流存在明显的各向异性特征,因此,针对存在浅水植物的复式河道流动特性的各向异性数值模拟研究是今后需要开展的工作。
[1] 张明亮.近海及河流环境水动力数值模拟方法与应用[M].北京:科学出版社,2015.
[2] SU X H,LI C W.Large eddy simulation of free surface turbulent flow in partly vegetated open channels[J].International Journal for Numerical Methods in Fluids,2002,39(10):919-937.
[3] WILSON C A M E.Flow resistance models for flexible submerged vegetation[J].Journal of Hydrology,2007,342(3/4):213-222.
[4] LI C W,ZHANG M L.Numerical modeling of shallow water flow around arrays of emerged cylinders[J].Journal of Hydro-environment Research,2010,4(2):115-121.
[5] ASAEDA T,RASHID M H.The impacts of sediment released from dams on downstream sediment bar vegetation[J].Journal of Hydrology,2012,430-431:25-38.
[6] BENJANKAR R,EGGER G,JORDE K,et al.Dynamic floodplain vegetation model development for the Kootenai River,USA[J].Journal of Environmental Management,2011,92(12):3058-3070.
[7] ASAMI K,AKAMATSU H,FUKUI S,et al.Morphological characteristics of flood refugia of cobble-bed vegetation[J].Journal of Hydro-environment Research,2012,6(2):127-136.
[8] GHANI U,ANJUM N,PASHA G A,et al.Numerical investigation of the flow characteristics through discontinuous and layered vegetation patches of finite width in an open channel[J].Environmental Fluid Mechanics,2019,19(6):1469-1495.
[9] 张明亮,沈永明.植被作用下复式渠道的三维湍流数值模拟[J].应用基础与工程科学学报,2009,17(3):402-411.
[10] 刘彦东,徐国宾,张雅卓.含柔性沉水植物河道水力特性三维数值模拟研究[J].水资源与水工程学报,2014,25(6):44-49.
[11] 黄本胜,谭超,陈晖,等.滩地种树对窄滩复式河道水动力特性的影响研究[J].水动力学研究与进展,2018,33A(3):329-336.
[12] ZHAO F,HUAI W X.Hydrodynamics of discontinuous rigid submerged vegetation patches in open-channel flow[J].Journal of Hydro-environment Research,2016,12:148-160.
[13] 杨克君.复式河槽水流阻力及泥沙输移特性研究[D].成都:四川大学,2006:82-89.
[14] 杨纪伟,胥战海,李书芳,等.基于FLUENT的明渠紊流边界层数值模拟[J].人民黄河,2009,31(1):30-31.