目前,海水养殖已由粗放型趋向于集约化发展,工厂化养殖具有不受气象灾害影响、高产量、高质量等特点,是海水养殖产业中一种经济效益较好、产品附加值较高的养殖模式,发展前景良好。工厂化养殖的目的是达到无污染、零排放、高密度、可持续发展的生态养殖,然而目前工厂化养殖生产成本依然很高,相关调研报告显示,工厂化海水养殖中煤电等传统能源成本占总成本的比例最高,已经达到30%以上[1],这说明目前能源成本已成为制约工厂化海水养殖发展的一个重要因素,为了更好地实现工厂化海水养殖的可持续发展,开发利用新能源和节能技术是必由之路。太阳能作为目前世界上应用前景最好的新能源之一,其研究热度不断攀升。太阳能具有总量巨大、分布广泛、清洁无污染的优点,而且开发利用太阳能不会过多占用宝贵的土地资源。但长期以来,制约太阳能产业发展的主要问题是其具有不连续、不稳定、利用效率低的缺点,而蓄热调峰技术则是解决这一问题的关键[2]。对于海水养殖行业来说,利用太阳能实现养殖池的精准控温可以有效降低设备的能耗成本,因此,开发用于海水养殖的蓄热技术尤为重要。
相变蓄热具有蓄热密度大、相变温区窄、可显著降低蓄热装置尺寸等优点,是极具应用潜力的一种蓄热方式[3]。Tamme等[4]在1991年提出了太阳能蓄热系统的开发,对蓄放热过程进行了适用的系统设计;然而,由于常用相变蓄热材料(phase change materials,PCM) 的导热系数比较低,导致相变蓄热装置的换热性能较差。有效提高相变蓄热装置的充、放热速率是其大规模应用所要解决的首要问题[5],而作为相变蓄热技术研究热点之一的梯级相变蓄热(Cascaded Thermal Energy Storage with phase change materials,CTES)能有效强化传热。CTES是按照“温度对口、梯级利用”的原则,在放热流体的流动方向上布置熔点依次降低的不同相变蓄热材料[6]。研究显示,在单一PCM传热模型中,PCM完全液化后在轴向方向有温度梯度,梯级相变蓄热放热流体与相变蓄热材料之间的传热温差尽可能保持不变,从而缩短相变蓄热材料蓄热时间。CTES装置的研究开始于1989年,Farid等[7]对相变材料的梯级组合与单一PCM进行了传热效率的理论计算比较,结果表明,PCM的梯级组合较单一PCM传热效率提高15%。近些年的研究则以基于CFD的数值模拟研究为主,Michels等[8]应用CFD数值模拟对梯级和单级蓄热装置进行了比较,结果表明,梯级蓄热较单级蓄热PCM熔化速度和储热量都增大;Adine等[9]对LTES中的导热流体(HTF)参数进行研究后认为,HTF的温度和质量流率都对CTES的优化起重要作用;Fang等[10]在忽略蓄热装置形式的前提下,对PCM质量组分进行数值模拟研究后认为,PCM质量组分的优化对提高CTES蓄热性有一定作用。随着研究的深入,研究者们开始注意到PCM熔化过程中自然对流对传热的影响,王艺斐[11]在考虑自然对流情况下对CTES与单级相变蓄热装置进行了比较,结果表明,梯级较单级储热量增加58%;Longeon等[12]对装有石蜡RT35的环形潜热储存单元进行了实验和数值研究,建立了一个可视化的测试回路,用于分析系统中传热流体(HTF)注入侧的流动情况,并对充放热结果进行了解释,结果表明,注入侧与自然对流换热机制的耦合影响了相变材料熔化前沿的演变;Pahamli等[13]研究了在管壳式换热器中纳米材料的分散度和倾角对相变材料熔化的影响后认为,合理选择纳米材料的分散度和倾角对提高换热效率有积极作用。
以上研究表明,CTES内部传热效率受到多方面因素影响,而传热效率的提高依赖于对内部传热特性的细致分析,但是目前研究中大多是对蓄热装置总体指标如总储热量和总液相率等的研究[14],缺乏对内部传热的细致研究和讨论。另一方面,由于水产养殖生物的生存环境一般需要保持恒定的水温,为减小养殖水体温度的波动,要求太阳能相变蓄热系统在一天内尽可能多地进行蓄放热过程。简单的单级相变蓄热单元因其蓄放热时间长,并不能满足实际生产要求,而梯级相变蓄放热结构,在保持一定蓄热量的同时可减少蓄放热时间,非常适用于海水养殖等相关领域。然而,对CTES的研究目前仍集中于基础研究或面向传统工业领域,并未涉及海水养殖或其他海洋相关产业领域,而后者本身也有着较高的能量需求,甚至海洋本身也蕴含着巨量的能源。因此,结合海水养殖等海洋产业应用需求,设计高效梯级相变蓄热装置,并探究装置中每级PCM的内部传热机理,对了解梯级相变蓄热过程中PCM的动态变化和指导海洋产业节能减排的工程实践有重要意义。
本研究中,根据工厂化海水养殖中能量需求的实际特点,应用梯级相变蓄热的能源管理理念,参考目前应用最为广泛的管壳式换热器,设计可用于海水养殖行业的高效梯级相变蓄热装置模型,并基于焓法模型,运用有限容积法[15]数值模拟了梯级相变蓄热装置的充热过程,分析自然对流情况下三级PCM的平均液相率变化,以及PCM内部监测点温度、流速随时间的变化,旨在揭示梯级相变蓄放热装置内部的传热特性,推动其在海水养殖生产中的大规模应用。
1 模型及控制方程
1.1 材料选择
太阳能集热器内部温度往往高于100 ℃,为提高集热与传热效率,生产实践中常选择具有更高沸点的导热油作为传热流体。本研究中所选HTF沸点为310 ℃,密度为953 kg/m3,比热容为2084.6 J/(kg·K),导热系数为0.316 2 W/(m·K),黏度为0.001 86 kg/(m·s)。
选择目前研究较为成熟的石蜡作为相变材料,其过冷度较小的特点便于数值模拟分析。由于冬季是海水养殖中加热控温的主要时间段,在此期间,蓄热系统管道中HTF入口温度常位于100 ℃左右,因此,为提高HTF与PCMs之间的热流密度,并结合养殖池的实际控温需求(20 ℃)左右,本研究中以相变温度为50 ℃左右的3种石蜡材料(C20、C24、C28)作为PCMs,从左至右按熔点降低的顺序依次填充到各级PCM(PCM1、PCM2、PCM3)内,相变温度呈梯度变化,PCM相关物性如表1所示。
表1 相变材料热物性参数
Tab.1 Thermophysical parameters of phase change materials

石蜡材料paraffin material密度ρ/(kg·m-3)density比热Cp/(kJ·kg-1·K-1)specific heat capacity导热系数λ/(W·m-1·K-1)coefficient of thermal conductivity运动黏度μ/(kg·m-1·s-1)kinematic viscosity热膨胀系数β/K-1coefficient of thermal expansion比内能γ/(kJ·kg-1)specific internal energy熔点Ts/Kmelting pointC207782.000.1510.780.00076247309.85C247802.120.1510.780.00076253324.65C287802.120.1510.780.00076253334.25
1.2 物理模型
本研究中的物理模型如图1所示,模型为多级管壳式蓄热装置,HTF在外管流动。
由于海水养殖业对蓄放热速率要求较高,通常蓄放热半周期应在2~5 h,为提高材料利用率,尽可能保证热能以潜热形式存储与释放,利于恒定控温,换热器管径不宜过大,长度不宜过长。本研究中设计的换热器模型,内径r为175 mm,外径R为225 mm,3组装置长度(L1、L2、L3)均为1380 mm,模型总长(L)为4340 mm。HTF由左上进口处进入装置,由右下出口处流出。并对计算模型提出如下假设:
(1)忽略空穴和辐射的影响;
(2)忽略管壳的管壁厚度,内壁传热,外壁和侧壁绝热;
(3)PCM物性保持恒定且有各向同性和均质。
根据研究内容,在模型中设置了27个监测点,每级PCM均为9个,并均布于PCM内部,具体位置如图1所示。
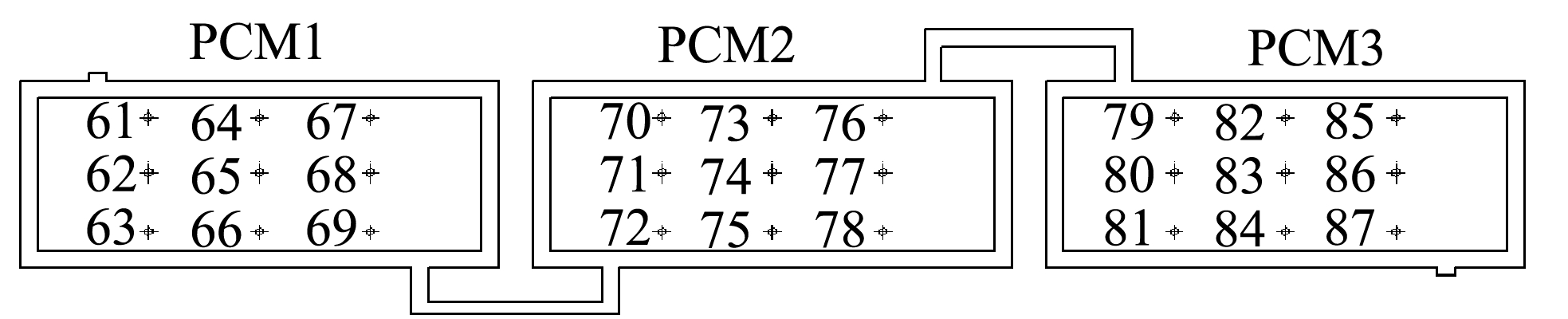
图1 物理模型及监测点位置分布
Fig.1 Physical model and location of monitoring points
1.3 数学模型
建立数学模型时,PCM1、PCM2、PCM3内部传热方式为热传导和自然对流。
1.3.1 HTF域 HTF的控制方程如下:
连续性方程:![]()
动量方程:![]()
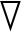 ·[μf(
·[μf(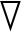 V+(
V+(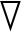 V)T)];
V)T)];
能量方程:![]()
其中:V、ρf、μf、Cpf、kf、p、T分别为HTF的流动速度、密度、动力粘度、比热、导热系数、压力、温度。
1.3.2 PCM域 PCM的控制方程如下:
连续性方程: 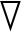 ·V=0;
·V=0;
动量方程:![]()
其中,达西动量源项定义如下:
当PCM凝固时,PCM流速强制为0[16]。目前的研究中,Amush和λ一般分别取为105和10-3[17]。f代表液相率,其定义与取值范围如下:
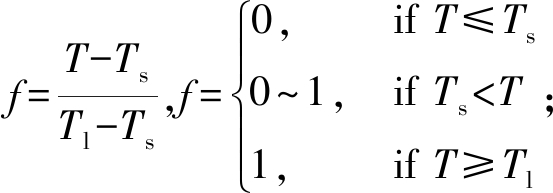
能量方程:![]()
1.4 边界条件
PCM在进口和出口的边界条件:
![]()
内表面的边界条件:
外表面的边界条件:![]()
2 网格无关性验证及fluent设置
2.1 网格无关性验证
为验证网格无关性,进行了网格数分别为38 030、68 881、86 544、153 170、219 653的模型在相同条件下的数值模拟,并在PCM3的上中下三部分各提取了一个监测点(point80、point82、point84)数据进行对比分析(图2-A、B、C),结果显示,除网格数最少(38 030)的模型外,其余网格数模型的模拟误差均在5%以内,均满足网格无关性要求。考虑精度和简便计算要求,选择网格数为86 544的模型进行模拟。

图2 网格无关性验证
Fig.2 Grid independence verification
2.2 Fluent设置
根据本文研究对象,选择单精度求解器进行fluent计算,为获得充热效率等数据,选择瞬态模型求解计算,并考虑了重力影响。由于实际生产中HTF多为湍流状态,因此,本文研究了HTF湍流状态下PCM与HTF的换热情况,而充热过程PCM内部的自然对流对传热有重大影响[18],故本研究中也考虑了PCM熔化时的自然对流现象。
根据传感器测量数据,冬季太阳能的热辐射可使管道中HTF温度达到100 ℃左右,故模型入口温度设置为373.15 K。此外,根据模型数据,水力直径为50 mm,根据下式计算湍流强度:
其中:I为湍流强度;Re为雷诺数。
根据当地企业太阳能集热器系统中实测的循环泵功率,设置模拟的入口流速为4 m/s,湍流强度为3.6 %。PCM和HTF之间壁面设置为流固耦合,求解方法选择二阶迎风格式。残差均在0.001以下,计算结果收敛,结果可信度好。
3 结果及分析
3.1 PCM液相率随时间的变化
根据太阳能系统的通用运行工况区间[19],选择HTF入口流速4 m/s、入口温度为100 ℃工况为例进行分析。
对于梯级相变蓄热的物理模型,由于各PCM的初始温度相同,其熔化速率会随着HTF沿流动方向的温度变化而产生明显的差异,如图3所示,PCM平均熔化时间沿HTF流动方向依次减少,PCM1完全熔化所需时间近18 000 s,PCM2约为12 000 s,PCM3只需约6000 s就能达到完全熔化,而PCM的熔化起始时间也呈现梯级规律,各级PCM熔化起始时间依次为PCM1 图3 液相率-时间曲线 图4为各级PCM内部温度-时间曲线,从图中可以看出,各级PCM(PCM1、PCM2、PCM3)上、中、下部各自3个监测点的温度比较接近,总体上差异不大,因此,在后续不同PCM之间的性能比较中,可选择各级蓄热器沿HTF流动方向中段位置的监测点进行分析。对于PCM上部温度,上升过程均较中下部稳定,在达到相变点之前,温度上升速度较快;相变点以后直至达到温度上限(365 K)期间,温度曲线渐趋平缓,其上升速度逐渐下降(图4-A)。对于PCM中部温度,起初有一个时间不太长的“准备期”,期间温度一直维持在初始温度,随后温度稳定快速上升,直至在相变点上方区域形成一个长达数千秒的温度平台,温度曲线在整个平台区间有较大波动,随着温度再度开始上升,温度波动的幅度也有所减弱(图4-B)。而对于PCM下部温度,起初均有一个5000 s左右的较长“准备期”,随后温度稳定快速上升,上升速率与上部相近,当温度达到中部平台温度后,两者曲线重合,并以相近的波动幅度继续平缓上升(图4-C)。 图5为PCM内部速度-时间曲线,在传热初始阶段,PCM各部分流动速度接近为零,经过一段时间后,速度开始增加,并产生明显的波动,各部分速度均会在达到相应峰值后减小到相对稳定的状态,并以一个相对稳定的幅度波动。PCM各部分达到相变的时间随HTF流动方向逐渐降低,其中上部间隔500 s左右,平均时间间隔的顺序为PCM上部 图5 各级PCM内部速度-时间曲线 图4 各级PCM内部温度-时间曲线 液相率变化表征了换热器内部相变与热传递过程的整体平均情况,但无法描述局部及不同位置之间的变化差异,故不足以提取足够的装置优化所需的信息。本文中将围绕换热器内部不同监测点传热特征之间的差异进行比较分析,寻找梯级相变换热器优化设计的依据。 图6为各PCM内部纵向中线监测点温度-时间曲线,不同PCM中线监测点的温度变化拐点与速率均保持着与液相率变化一致的趋势。通过横向对比,PCM上部和中部相同位置监测点的温度曲线呈现出明显的梯级规律(图6-A、B),而底部监测点的梯级规律并不明显(图6-C),可能的原因是底部由于自然对流作用,其温度并不能平缓的升高,而在自然对流发生阶段,底部热量向上传递,导致其温度曲线出现波动。 图6 各级PCM纵向中线监测点温度-时间曲线 图7为各PCM内部纵向中线监测点速度-时间曲线,PCM上中下各部分的中线监测点速度峰值时间点均为PCM3 图7 各级PCM纵向中线监测点速度-时间曲线 图8为换热器不同传热时间温度云图,随着传热时间的增加,PCM温度从四周向内部不断增加,并出现非四周向中心方向的温度梯度和不均匀性(图8-B、C、D、E),当PCM中部温度达到相变点后,温度出现大范围不均匀性(图8-F、G、H),随后温度进一步上升并逐步达到均一(图8-I、J)。 从整个过程来看,温度分布云图清晰地显示了PCM熔化过程中的温度演化过程,进一步证明自然对流现象伴随着整个PCM熔化过程。当HTF刚进入换热器时,还来不及向PCM传热,因而没有熔化及自然对流现象(图8-A)。随后,各PCM的边缘温度均开始快速上升,产生较大的温度梯度,其中PCM3的温度上升明显快于PCM1及PCM2。很快在被加热区域内出现了局部温度不均匀性及非重力方向的温度梯度,同时,一些熔化的高温PCM微团开始向上漂移,形成了下部与中部之间的对流通道。由于自然对流的强化传热作用,换热器中部温度会较中部与上部之间的温度上升更快,而此时双向的快速传热导致下部各点温度暂时达到平衡,也就进入了平台阶段。当换热器内部相变整体刚完成时,大面积的温度不均匀性仍然存在,但由于相变吸热已经结束,不均匀性在对流中被迅速消除,这解释了温度平台终点处,波动明显加剧,甚至下部温度出现大幅下降的现象。 图8 梯级相变蓄热装置不同时刻温度分布云图 梯级相变蓄热特点是HTF与PCM之间的温差在流动方向上保持一致,以使得各PCM传热速率尽可能相近,但本模型所获得的各PCM传热平均温差并不一致,因而导致了PCM中部的平台温度与相应相变点的温差不一致,随HTF/PCM传热温差的增大而增大(图4)。 目前海水养殖产业中太阳能的蓄能设施较少,本文中设计的梯级相变蓄热模型,经模拟计算其蓄热时间能够达到海水养殖产业应用的要求,具备进一步研究应用的潜力。在目前梯级相变蓄热的数值模拟和试验研究中已有对自然对流现象的讨论,王艺斐[11]在考虑自然对流影响情况下发现梯级相变蓄热较单级更优,Longeon等[12]通过试验验证了自然对流对熔化过程具有重要影响。本文中通过数值模拟,验证了自然对流状态的形成与发展对梯级相变换热器的性能起着主导作用,大大加速了换热器中的传热过程,并促使各部分能量快速达到均衡一致。由于各PCM相变温度及位置差异,熔化起始时间由PCM3到PCM1逐级增加,但自然对流的作用使各级PCM之间在充热过程中相变能力的差距显著缩小,使其更接近于理想的运行条件,突出了梯级相变蓄热“温度对口、梯级利用”的本质优势。 本文中通过在每级PCM(PCM1、PCM2、PCM3)中分别按上中下3个部分设置3个监测点,共设27个监测点,更为细致和全面地分析了梯级相变蓄热装置每级PCM内部的传热特性差异。各监测点温度和速度曲线的波动均显示,在管壳式梯级相变蓄热装置传热前期,其内部以热传导为主要的传热方式,中后期自然对流现象明显,这一点在Prasad等[18]所建立的梯级相变复合对流-传导模型中也得到了证明。在此基础上,通过对内部多个监测点数据的分析发现:梯级相变蓄热装置每级PCM内部的传热过程有一定差异,每级PCM上中下不同位置的升温速度也存在差异;此外,结合对监测点温度和流速曲线的分析,推测换热器内部石蜡在熔化过程中存在漂移现象,使得PCM下部与中部之间形成了双相毛细结构,显著促进了HTF与PCM及PCM中部与下部之间的换热,这一点在文献中相关研究较少,对于该现象的细节及其与HTF入口流速、入口温度等条件的关系,在后续的模拟计算中会进行相关的讨论。从模型的实际应用来看,虽然自然对流现象可有效削弱各PCM显热阶段热存储量及历时差异所造成的不利影响,但距离梯级相变蓄热的理想效果仍有差距,因此,有必要通过增加肋片等方式[20],改善高温PCM换热器的导热能力,缩小系统换热时间区间。根据模拟结果,建议在CTES设计过程中,适当改变HTF的流道分配等因素,使热量更多地从换热器下方传入,有利用增强自然对流,缩减系统相变时间。 (1)管壳式梯级相变蓄热装置在充热前期内部传热以热传导为主导,中后期自然以对流为主导。 (2)每个部分的PCM上中下三部分都有较显著的传热差异,PCM3熔化速度较PCM2和PCM1快,PCM下部与中部之间的对流传热是影响换热器整体相变速率的关键。 (3)通过分别研究每个PCM内部传热特性,梯级相变蓄热装置的传热特性得到更深入的阐述,其结果可为高效梯级相变蓄热装置结构优化设计提供参考,为高效梯级相变蓄热技术在海水养殖行业的推广应用提供助力。 本研究结果可为高效梯级相变蓄热装置结构优化设计提供参考,为高效梯级相变蓄热技术在海水养殖行业的推广应用提供助力。 [1] 赵鹏,李贤,周兴,等.海水工厂化养殖能耗及新能源应用调研分析[J].渔业现代化,2011,38(2):21-26. [2] 侯宏娟,郑天帅.含蓄热的太阳能辅助供热机组供暖期调峰性能分析[J].太阳能学报,2018,39(7):1807-1814. [3] 李亚奇,何雅玲.单级相变蓄热装置的火用效率分析与优化[C].北京:中国工程热物理学会-工程热力学与能源利用,2013. [4] Tamme R,Taut U,Streuber C,et al.Energy storage development for solar thermal processes[J].Solar Energy Materials,1991,24(1-4):386-396. [5] 夏立荣,岳希明,刘敏珊.换热器夹套式变截面导流筒数值模拟与结构优化[C]//第三届全国换热器学术会议论文集.长沙:中国机械工程学会,2007. [6] 胡芃,卢大杰,赵盼盼,等.组合式相变材料最佳相变温度的热力学分析[J].化工学报,2013,64(7):2322-2327. [7] Farid M M,Kanzawa A.Thermal performance of a heat storage module using PCM’s with different melting temperatures:mathematical modeling[J].Journal of Solar Energy Engineering,1989,111(2):152-157. [8] Michels H,Pitz-Paal R.Cascaded latent heat storage for parabolic trough solar power plants[J].Solar Energy,2007,81(6):829-837. [9] Adine H A,Qarnia H E.Numerical analysis of the thermal behaviour of a shell-and-tube heat storage unit using phase change materials[J].Applied Mathematical Modelling,2009,33(4):2132-2144. [10] Fang Ming,Chen Guangming.Effects of different multiple PCMs on the performance of a latent thermal energy storage system[J].Applied Thermal Engineering,2007,27(5-6):994-1000. [11] 王艺斐.串联式多相变储热实验与数值模拟研究[D].北京:中国科学院研究生院(工程热物理研究所),2016. [12] Longeon M,Soupart A,Fourmigué J F,et al.Experimental and numerical study of annular PCM storage in the presence of natural convection[J].Applied Energy,2013,112:175-184. [13] Pahamli R,Hosseini M J,Ranjbar A A,et al.Effect of Nanoparticle dispersion and inclination angle on melting of PCM in a shell and tube heat exchanger[J].Journal of the Taiwan Institute of Chemical Engineers,2017,81:316-334. [14] 于丹,曹勇,曾范梅.组合式相变材料换热器储热速率的实验研究[J].暖通空调,2008,38(5):65-67. [15] 张磊成,果晓东,赵恩铎,等.计算流体力学(CFD)发展简述[C]//北京力学会第二十三届学术年会会议论文集.北京:北京力学会,2017. [16] Voller V R,Prakash C.A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems[J].International Journal of Heat and Mass Transfer,1987,30(8):1709-1719. [17] Tiari S,Qiu Songgang.Three-dimensional simulation of high temperature latent heat thermal energy storage system assisted by finned heat pipes[J].Energy Conversion and Management,2015,105:260-271. [18] Prasad J S,Muthukumar P,Anandalakshmi R,et al.Comparative study of phase change phenomenon in high temperature cascade latent heat energy storage system using conduction and conduction-convection models[J].Solar Energy,2018,176:627-637. [19] 张喜明,卞彩侠.太阳能直接供暖运行工况分析[J].能源与环境,2014(1):69-70. [20] 李革,于功志,程木军,等.提高翅片管式换热器热力性能的方法[J].大连水产学院学报,2006,21(1):68-71.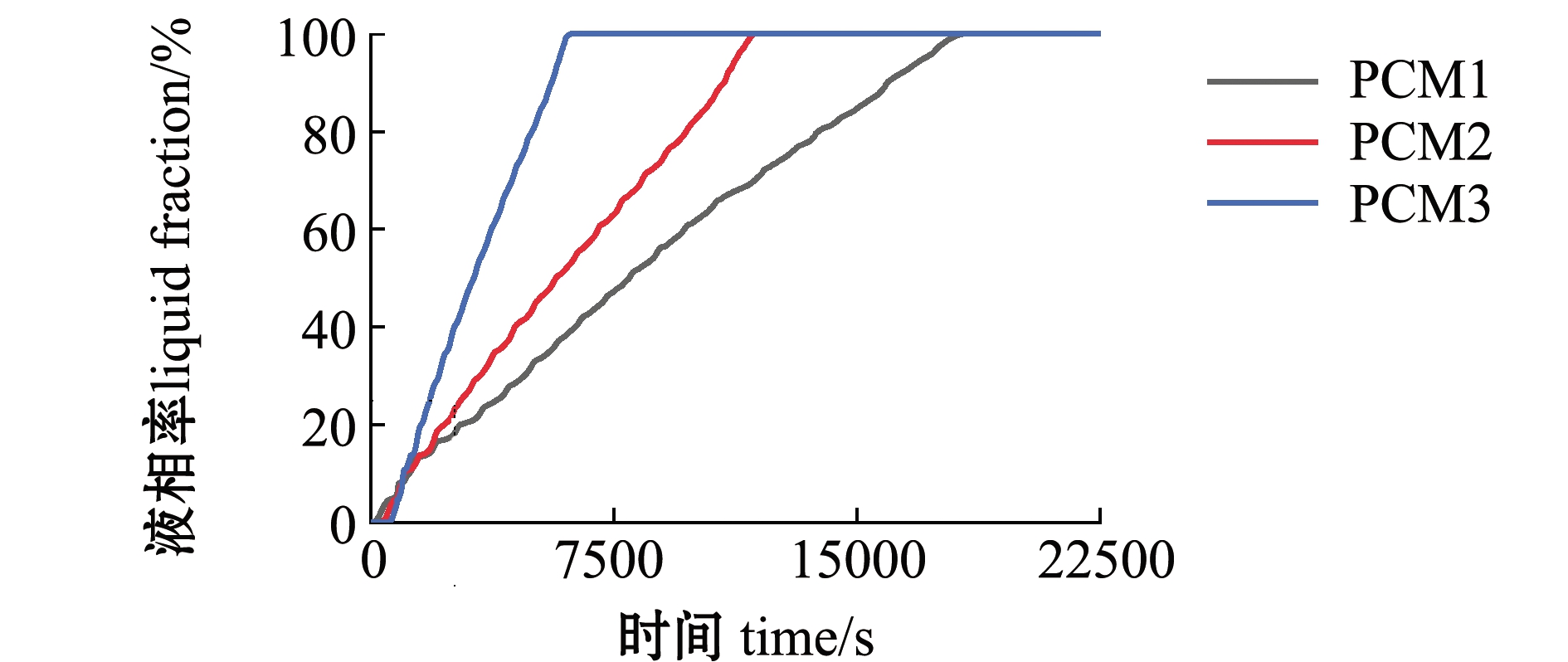
Fig.3 Liquid fraction-time curve3.2 充热过程中各级PCM内部监测点温度与流速的变化
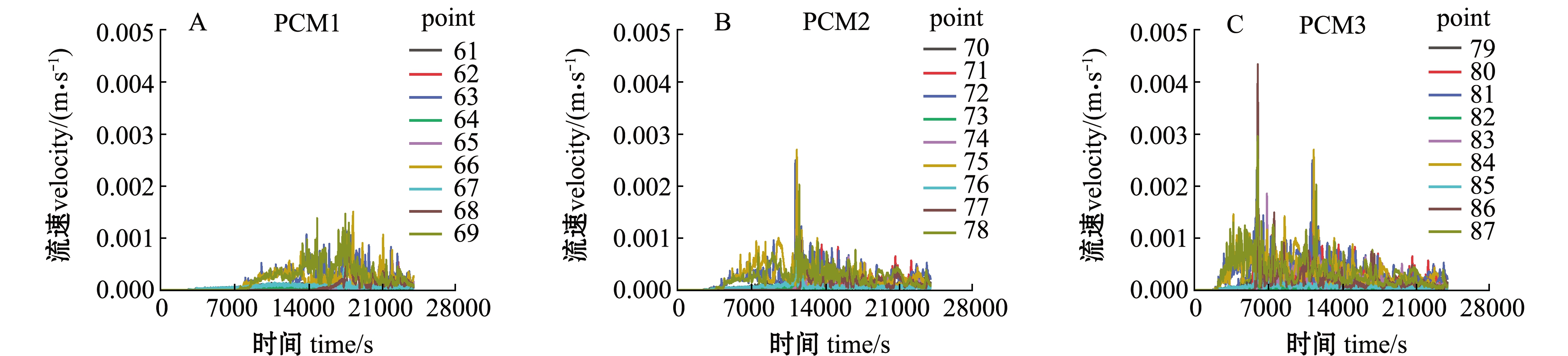
Fig.5 Internal velocity-time curves of each PCM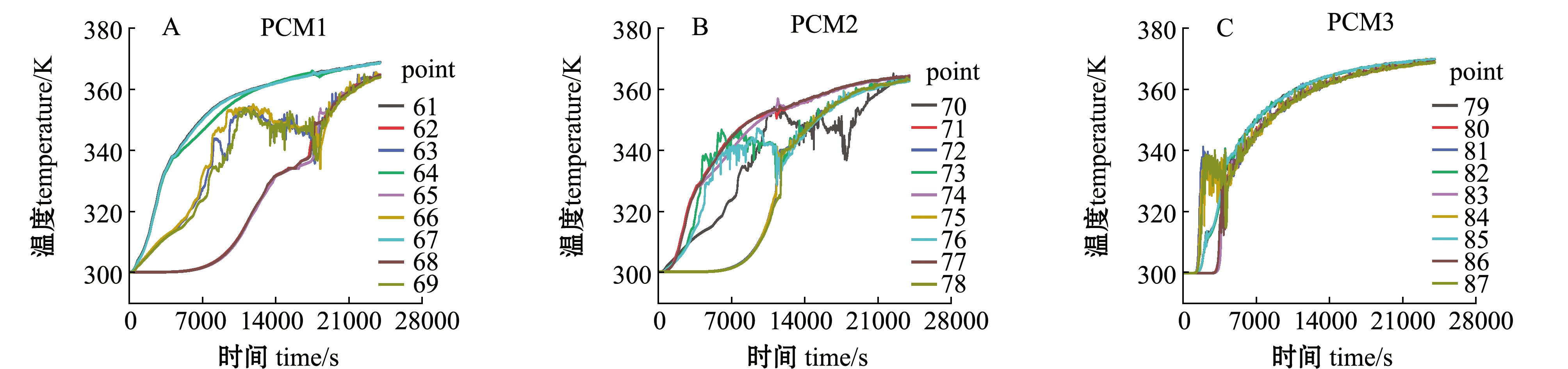
Fig.4 Internal temperature-time curves of each PCM3.3 充热过程中PCM内部及各级PCM之间传热比较

Fig.6 Temperature-time curves of longitudinal center line monitoring point of each PCM
Fig.7 Velocity-time curves of longitudinal center line monitoring point of each PCM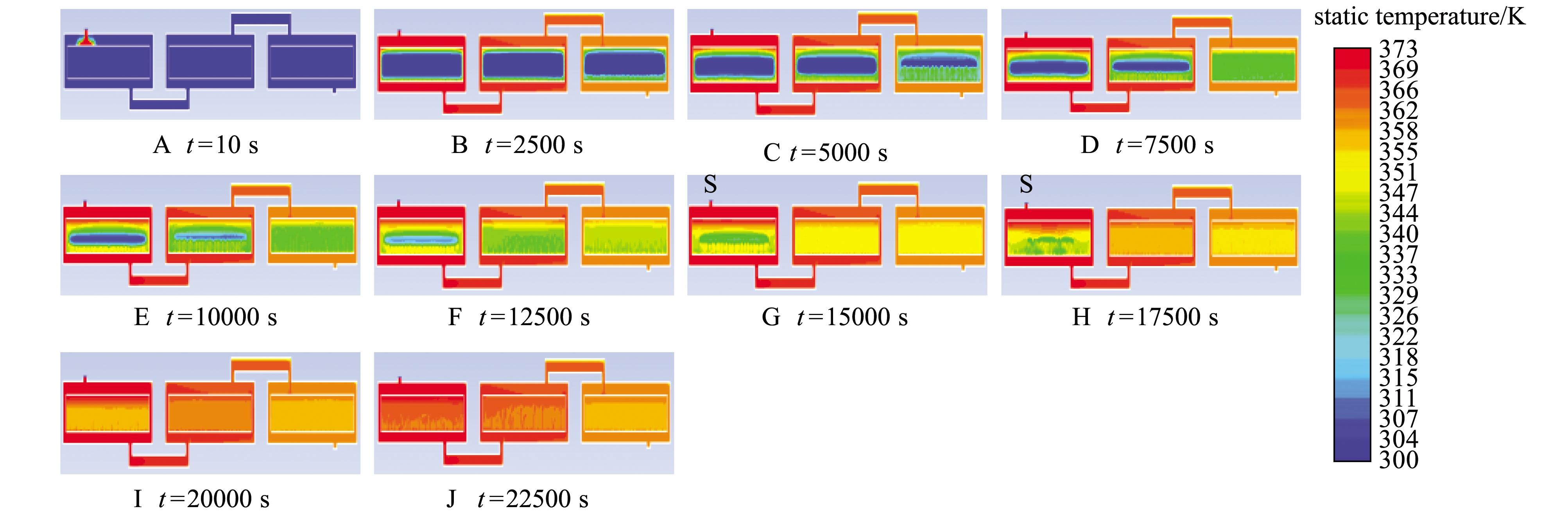
Fig.8 Temperature distribution nephogram of cascade phase change thermal storage device at different times4 讨论
4.1 用于海水养殖的管壳式梯级相变蓄热模型
4.2 PCM内部多监测点的设置与分析
5 结论