渔船是一种重要的海洋渔业生产工具,渔船的运行轨迹中包含了渔船的时空分布信息[1],通过分析渔船轨迹数据可以发现渔船的运动规律、行为模式、作业方式等[2],对精准掌握渔船作业行为[3]、保障渔船作业安全[4]、发现渔船异常行为、规范渔业执法等具有重要意义[5]。
船舶自动识别系统(Automatic Identification System,AIS)是强制在客船、货船、自航船舶和港作拖船上配备的一种船载装置[6],目的在于识别和跟踪船舶,避免船舶碰撞,保障航行安全[7]。AIS系统借助GPS和传感器向岸基站和其他船舶发送船名、呼号等静态信息和船位、航向、航速等动态信息[8],其中船位信息能够较好地描述船舶的轨迹,是船舶轨迹数据的主要来源之一[9],因此,通过挖掘AIS数据进行船舶轨迹分析成为船舶轨迹分析的重要方法之一[10]。由于AIS数据的发布频率很高,通常为几秒到几分钟发布一条[11],系统中产生了海量的AIS数据,大大增加了数据存储和分析的工作量,因此,需要有效的AIS轨迹数据压缩算法对海量AIS轨迹数据进行处理[12]。
轨迹数据压缩是指利用压缩算法将轨迹简化,去掉冗余的点,在确保不丢失轨迹特征信息的基础上尽可能降低存储代价[13]。Douglas等[14]提出Douglas-Peucker算法(简称为D-P),算法核心是连接初始轨迹的起点和终点,计算所有的点到直线的距离,再与固定阈值做比对,通过迭代用若干个线段代替原始轨迹,但该算法无法压缩动态信息。为此,李名等[15]提出动态D-P算法,在D-P算法基础上加入时间维,将原始轨迹按停泊点分段后在三维空间进行压缩,保留了更多轨迹特征,但是分段后的每段轨迹仍使用经典D-P算法,算法效率上没有突破。张树凯等[16]对比了不同阈值下经典D-P算法的压缩率,得出不同的阈值可得到不同的压缩效果,不同的海域条件可以选择不同的阈值压缩。徐凯等[17]在动态D-P算法基础上提出快速D-P算法,将算法对应到向量空间中,利用向量的几何性质对算法做出改善。由于D-P算法需要明确轨迹的起点和终点,不适用于实时数据,且复杂度较高[18]。Keogh等[19]提出Sliding Window算法(简称为SW),主要思想就是从轨迹起点开始,初始化一个大小固定的窗口,以数据流的形式逐步输入轨迹点,应用逐步压缩的思想实现在线压缩。高邈等[20]对SW算法进行改进,加入风流压差角来降低误差,但局部处理考虑不到部分特征点对轨迹形态的重要性。宋鑫等[21]提出动态阈值结合全局优化的压缩算法,通过停留点将轨迹分为若干个轨迹段后获取特征点,再利用改进SPM算法进行全局优化。
上述轨迹压缩算法多数在利用船位信息的基础上使用了AIS数据中提供的航速、航向和航行状态等信息,对于压缩AIS数据质量较高的商船轨迹数据能够取得较好的效果。但在对渔船AIS数据进行分析过程中发现存在属性数据丢失问题,如渔船在两个相邻时间点上的位置信息发生了较大变化,理论上讲该渔船的速度和航向大于0,但是获取的AIS数据中速度和航向数值却为0,这样利用航速、航向等属性信息的轨迹压缩算法不能实现对渔船轨迹的有效压缩。此外,渔船在捕捞作业过程中会以较慢的速度航行,特别是可能在某个区域来回慢速航行,所以渔船轨迹的压缩需要保留更多的特征点,这些特征点可能是后续进行轨迹分析的重要指标。因此,需要针对渔船轨迹的特点研究有效的渔船轨迹数据压缩算法。
本研究中针对渔船轨迹数据的特点,提出一种改进滑动窗口的渔船AIS轨迹压缩算法,利用相邻轨迹点之间的经纬度变化状态信息提取特征点,在算法中加入时间维,选择属性中的时间、经度、纬度属性,舍弃存在不确定性的属性,在保留特征点的同时,对密度较高的轨迹点进一步压缩,以实现停滞点直接压缩、运动点按比例压缩、作业点尽量保留的压缩目标。
1 数据特点与相关定义
1.1 渔船AIS轨迹数据特点分析
渔船AIS轨迹数据中主要包括静态信息和动态信息,静态信息包括船的信息识别码(MMSI)等,动态信息包括对地航速、船首向、航行状态、实时船位(经度、纬度)等[22],对船舶轨迹的信息属性解析如表1所示。
相对于在海上有固定航道的商船,渔船的轨迹数据有以下几个特点:
(1)数据点密度高。渔船捕捞作业过程中会在作业区域内以很慢的速度航行,在作业区停留时间较长,这将导致在作业区内渔船的AIS轨迹点分布密集,产生大量的轨迹数据,这将浪费存储资源和计算资源,每个轨迹点对应了一条数据。
表1 AIS轨迹信息表
Tab.1 Information on automatic identification system(AIS) trajectory
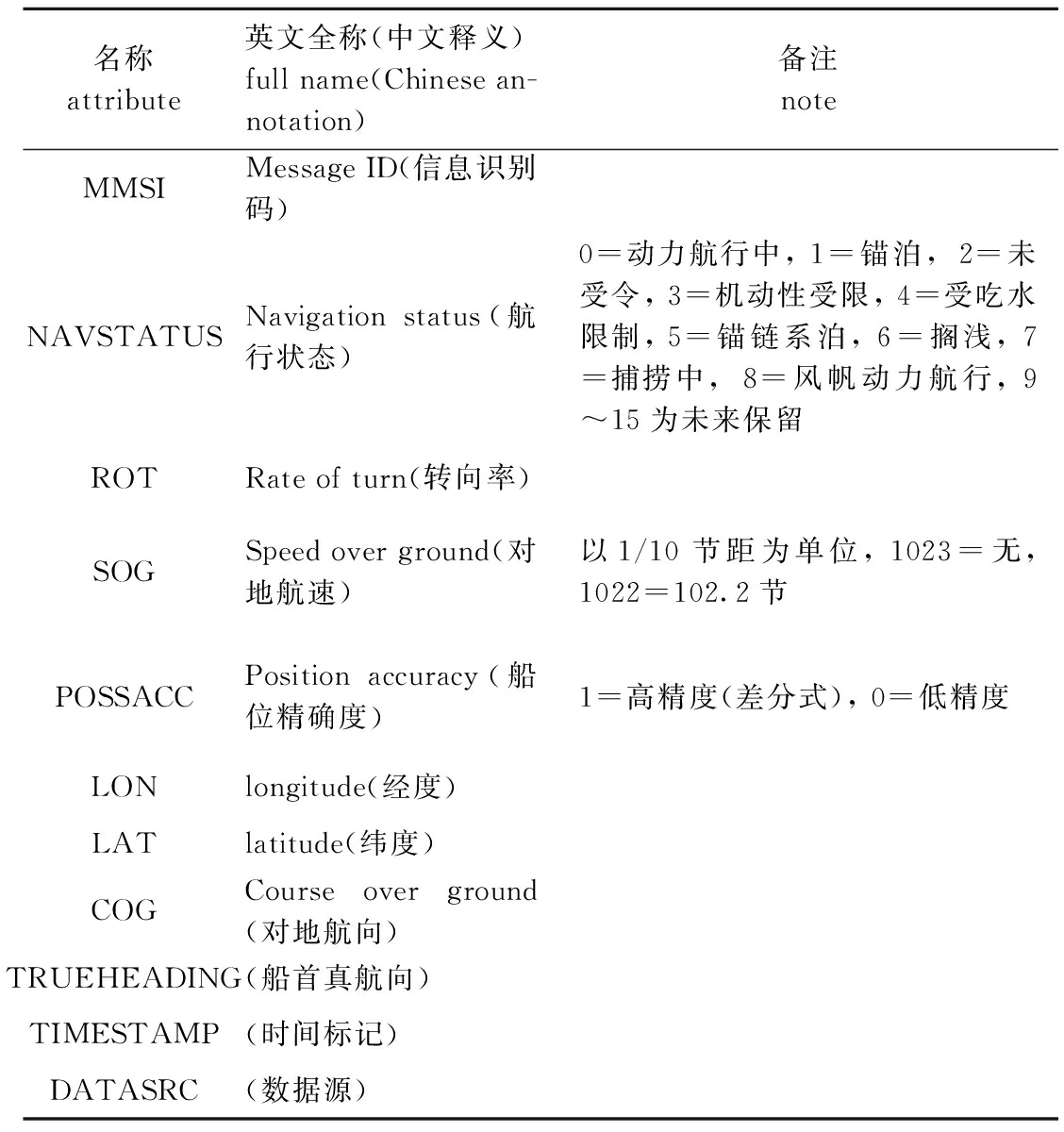
名称attribute英文全称(中文释义)full name(Chinese an-notation)备注noteMMSIMessage ID(信息识别码)NAVSTATUSNavigation status(航行状态)0=动力航行中, 1=锚泊, 2=未受令, 3=机动性受限, 4=受吃水限制, 5=锚链系泊, 6=搁浅, 7=捕捞中, 8=风帆动力航行, 9~15为未来保留ROTRate of turn(转向率)SOGSpeed over ground(对地航速)以1/10节距为单位, 1023=无, 1022=102.2节POSSACCPosition accuracy(船位精确度)1=高精度(差分式), 0=低精度LONlongitude(经度)LATlatitude(纬度)COGCourse over ground(对地航向)TRUEHEADING(船首真航向)TIMESTAMP(时间标记)DATASRC(数据源)
(2)部分AIS属性信息不准确。渔船的部分速度和状态信息会由于传感器故障在传送和接收的过程中发生数据缺失问题[23]。此外,经咨询渔船驾驶人员得知,AIS数据中的渔船状态信息是由人工输入的,可能存在状态数据不能完全准确描述渔船实际状态的情况。
(3)特征点数量多。如图1所示,由于渔船在捕捞作业时会多次在作业区往返航行,在航行过程中拐弯或掉头情况较多,这些点均为渔船的特征点,因此,与其他类别的船舶相比,渔船轨迹数据中特征点数量较多。
鉴于渔船AIS数据的上述特点,需要给出适合于渔船AIS轨迹分析的基本概念。
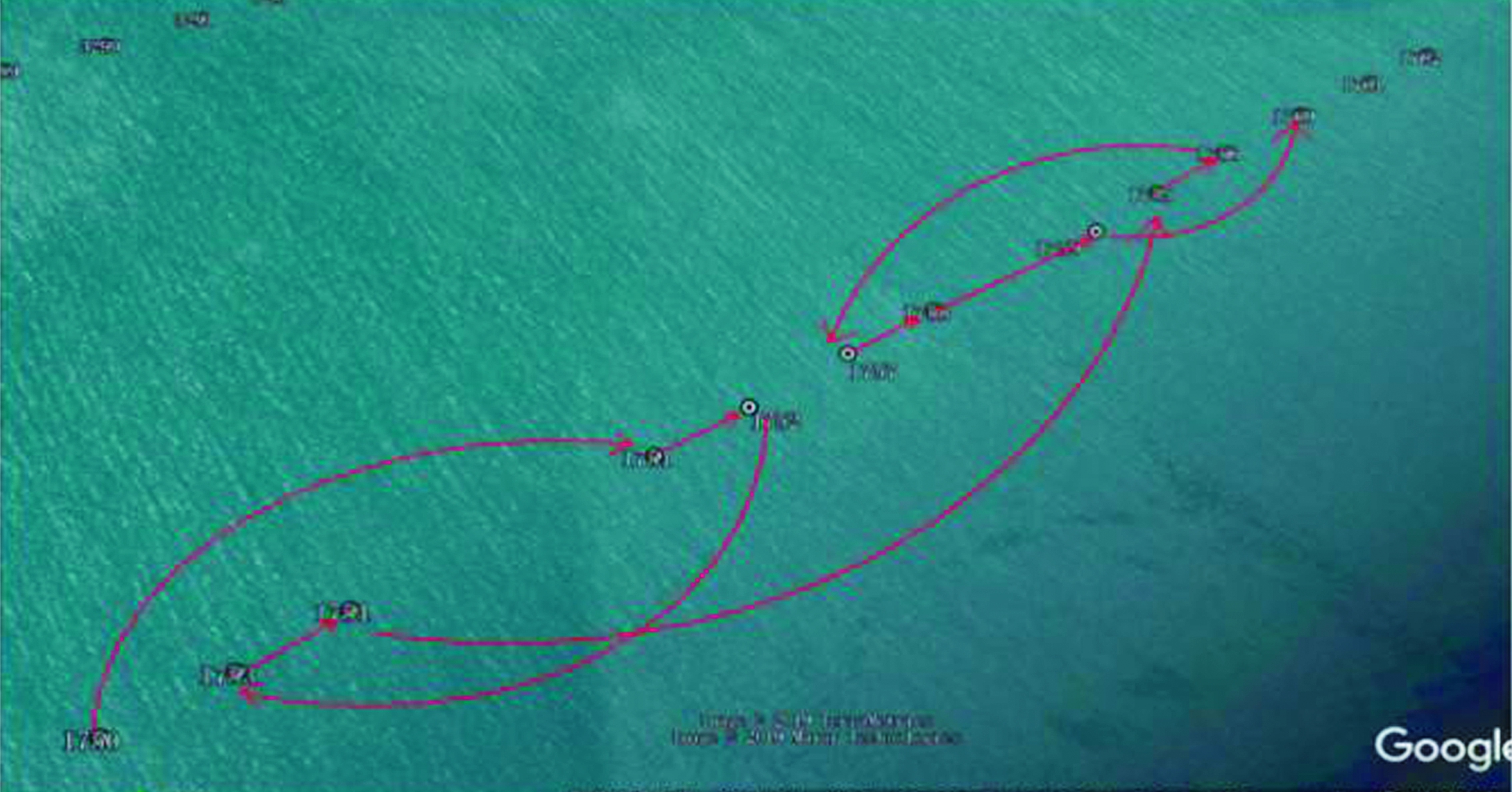
图1 渔船在捕捞时的航行特征
Fig.1 Sailing characteristics of a vessel during fishing
1.2 相关定义与公式
定义1 轨迹点:渔船的位置点用p表示,一个位置点含有3个属性信息:时间、经度、纬度,轨迹点表达式为
p=(x,y,t)。
(1)
其中:x、y分别为轨迹点的经度和纬度;t为时间。
定义2 原始轨迹:由原始轨迹点按照时间顺序排列起来的轨迹集合,用T表示,其表达式为
T={p0,p1,…,pn},i∈[0,n]。
(2)
其中:pi=(xi,yi,ti)表示原始轨迹点,对同一条船的轨迹T中的两个轨迹点存在ti<ti+1,0≤i<n。
定义3 经度差值和纬度差值:已知两个相邻的轨迹点pi(xi,yi,ti)和pi+1(xi+1,yi+1,ti+1),将两点经度或纬度坐标值作差,得出经度差值Δxi或纬度差值Δyi,即
Δxi=xi+1-xi,
(3)
Δyi=yi+1-yi。
(4)
定义4 特征点:在轨迹中令轨迹的经纬度趋势发生改变的点称为特征点,特征点集合用F表示。已知3个轨迹点pi、pi+1和pi+2,当经度趋势和纬度趋势中任意一个发生改变时,将点pi+2加入特征点集合F,表达式为
F={pi+2‖(ΔxiΔxi+1<0∪ΔyiΔyi+1<0)},
i∈[0,n]。
(5)
定义5 压缩轨迹:指对原始轨迹进行压缩处理后,去除了冗余的轨迹点,按照产生的时间顺序组成的新轨迹集合,用Tc表示,即
Tc={pc1,…,pci,…,pcn},ci∈[c1,cn],
tc1<…<tci<…<tcn。
(6)
定义6 停留点:在轨迹中,若渔船在某个位置进行长时间停留,即在某一区域有大量距离极近的轨迹点,则该位置的特征点称为停留点,用si(0<i<n)表示。
定义7 轨迹段:在原始轨迹T或者压缩轨迹Tc中,将点pi和pj连接组成的线段用pipj表示。
定义8 轨迹点距离PD:指两个相邻的轨迹点间的恒向线距离[24],计算公式为
(7)
c=Δyi/a,
(8)
(9)
由于恒向线是墨卡托投影上的直线,该线的长度就是沿恒向线两点之间的距离,其中a为等量维度,r为地球的半径。
2 渔船AIS轨迹数据压缩算法
Sliding Window算法是目前公认的经典算法,相比较于侧重轨迹全局形态的Douglas-Peucker算法等,该算法倾向于局部轨迹的优化压缩[25],渔船轨迹需要在压缩时保留更多的局部特征点,所以Sliding Window算法更加符合渔船轨迹的压缩宗旨。
2.1 Sliding Window算法
Sliding Window的算法思想是在起点初始化一个大小为1的滑动窗口,往窗口中逐步加入后续的轨迹点。将窗口内的第一个点和最后一个点连接,得到近似线段。计算近似线段与原始轨迹的垂直欧氏距离,若小于设定的距离阈值,则继续增大滑动窗口,大于阈值的点作为特征点保留,同时更新窗口直到窗口内的误差小于阈值,并重复以上步骤。
如图2所示,以p0为起点,初始化滑动窗口为{p0,p1}。以线段p0p2作为{p0,p1,p2}部分的近似轨迹,计算p1点和线段p0p2之间的垂直欧氏距离。若距离小于阈值,那么继续扩大窗口,加入新的轨迹点p3,滑动窗口为{p0,p1,p2,p3},以线段p0p3为近似轨迹,计算窗口内其他点的垂直欧氏距离。由于其距离超过设定的距离阈值,所以之前的窗口{p0,p1,p2}被选作近似轨迹的一段。接着以p3为新的滑动窗口起点,加入p3、p4,重复之前的步骤,直到轨迹终点。图中原始轨迹最终被简化为{p0,p2,p5,p8}。
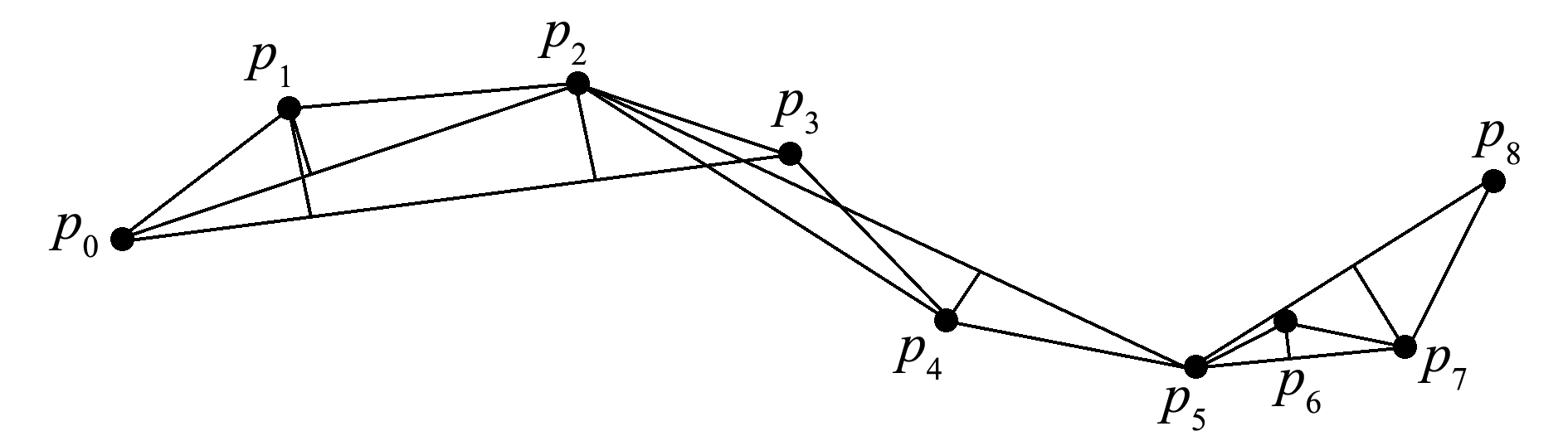
图2 Sliding Window算法
Fig.2 Algorithm of Sliding Window
2.2 基于改进滑动窗口的渔船AIS轨迹数据压缩算法
本文中针对渔船轨迹数据的特点,提出一种基于改进滑动窗口的渔船轨迹压缩算法,由于渔船轨迹数据中属性较多,且因为作业区信号丢失等问题导致渔船的航向状态、船首向等属性丢失或不准确,如表2所示,渔船的位置信息显示渔船处于运动状态,但速度和航向显示为0,说明该渔船存在属性丢失。 故本研究在算法中只使用准确的属性,既时间、经度和纬度,利用相邻轨迹点之间的经纬度变化状态信息提取特征点,解决Sliding Window算法在压缩频繁转向轨迹时出现的失真问题,并同时在算法中加入时间维,提高压缩的精准度。在初步保留特征点之后,对密度较高的轨迹点根据距离阈值进一步压缩,最终达到实现停滞点直接压缩、运动点按比例压缩、作业点尽量压缩的目的。
表2 信息丢失的轨迹样例
Tab.2 Sample of the lost-information trajectory
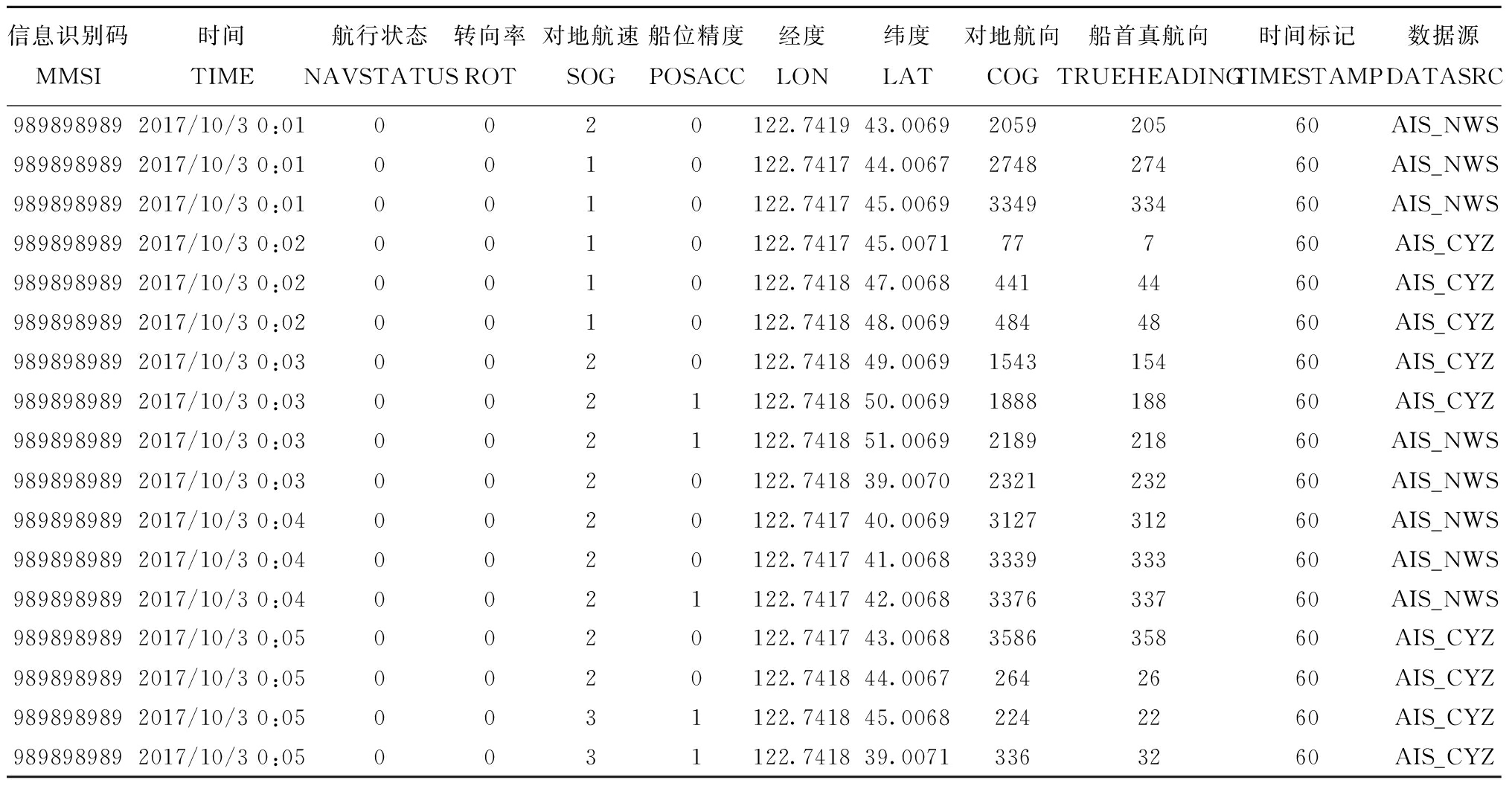
信息识别码MMSI时间TIME航行状态NAVSTATUS转向率ROT对地航速SOG船位精度POSACC经度LON纬度LAT对地航向COG船首真航向TRUEHEADING时间标记TIMESTAMP数据源DATASRC9898989892017/10/3 0:010020122.741943.0069205920560AIS_NWS9898989892017/10/3 0:010010122.741744.0067274827460AIS_NWS9898989892017/10/3 0:010010122.741745.0069334933460AIS_NWS9898989892017/10/3 0:020010122.741745.007177760AIS_CYZ9898989892017/10/3 0:020010122.741847.00684414460AIS_CYZ9898989892017/10/3 0:020010122.741848.00694844860AIS_CYZ9898989892017/10/3 0:030020122.741849.0069154315460AIS_CYZ9898989892017/10/3 0:030021122.741850.0069188818860AIS_CYZ9898989892017/10/3 0:030021122.741851.0069218921860AIS_NWS9898989892017/10/3 0:030020122.741839.0070232123260AIS_NWS9898989892017/10/3 0:040020122.741740.0069312731260AIS_NWS9898989892017/10/3 0:040020122.741741.0068333933360AIS_NWS9898989892017/10/3 0:040021122.741742.0068337633760AIS_NWS9898989892017/10/3 0:050020122.741743.0068358635860AIS_CYZ9898989892017/10/3 0:050020122.741844.00672642660AIS_CYZ9898989892017/10/3 0:050031122.741845.00682242260AIS_CYZ9898989892017/10/3 0:050031122.741839.00713363260AIS_CYZ
算法流程如图3所示。算法基本步骤如下:
(1)取一条渔船的轨迹数据。
(2)保留第一个轨迹点p0和最后一个轨迹点pn为特征点。
(3)以p0到p1的经纬度变化趋势为参照,相同方向航行的轨迹点经纬度变化呈现持续递增或递减趋势,趋势发生变化则考虑渔船在行驶中方向发生改变或者渔船的状态发生改变。分别比较相邻点之间的经度和纬度变化,只要二者有一项变化状态发生改变时,保留其为特征点。
(4)若在一定范围内的同一区域趋势频繁发生改变,考虑渔船是否处于静止或相对静止状态(停滞或捕捞状态),根据相邻轨迹点间距离判断是否处于停滞状态,相邻轨迹点之间距离小于3 m则直接压缩,直到得到一个距离大于3 m的点,重新开始判断。
3 验证试验
3.1 试验设计
为验证渔船AIS轨迹数据压缩算法的有效性,分别对单条渔船轨迹进行不同算法的压缩对比试验。算法采用Python语言编写,版本为3.6,IDE使用Spyder。
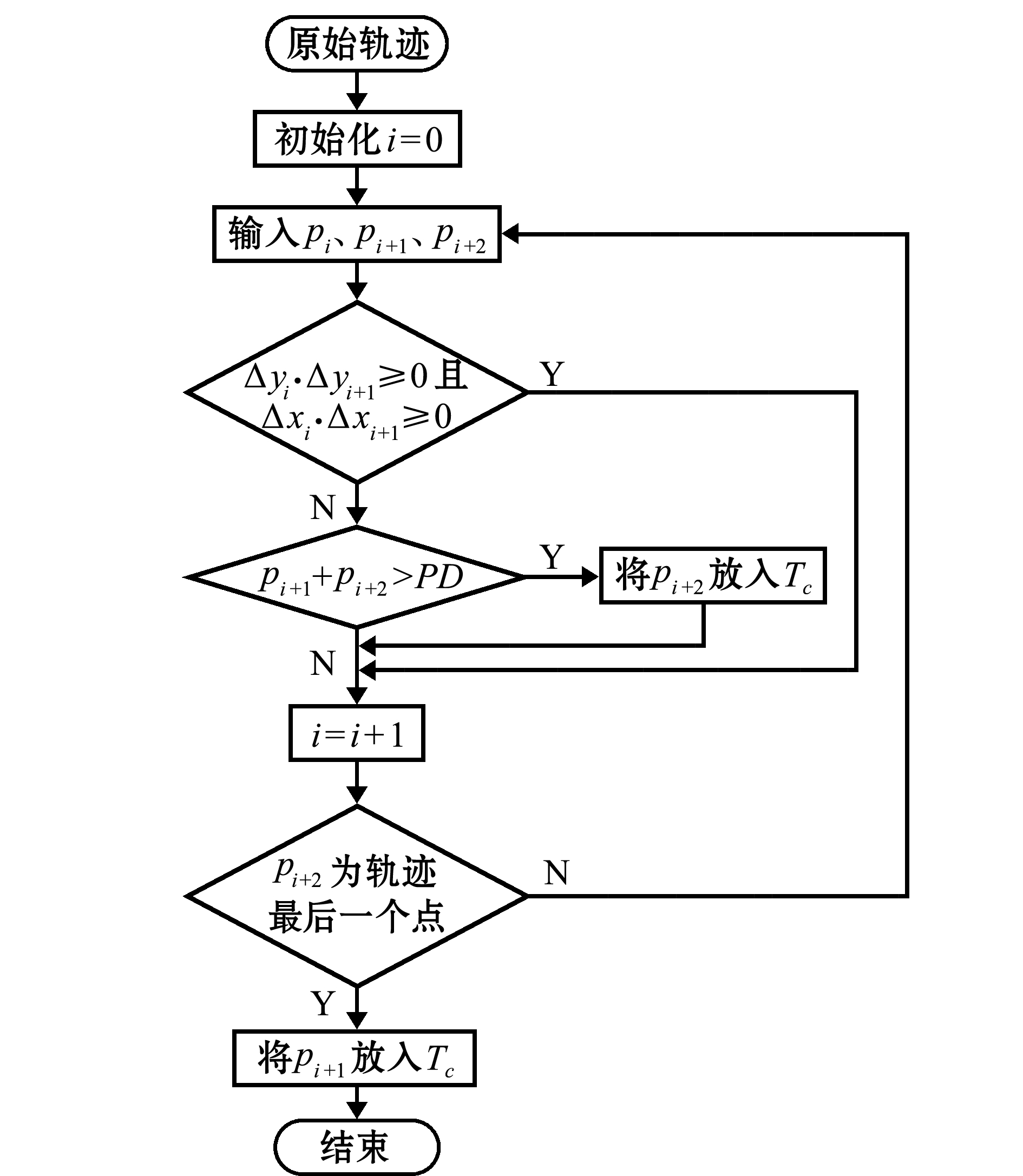
图3 基于改进滑动窗口的渔船轨迹压缩算法流程
Fig.3 Flowing chart of improved Sliding Window compression algorithm
原始试验数据集来自大连世想海洋科技有限公司,渔船轨迹数据以.csv的文件格式存储,时间跨度从2018年10月1日至2018年11月30日,大小约3.57G,原始数据样例如表3所示。
表3 原始轨迹数据样例
Tab.3 Sample of original trajectory data
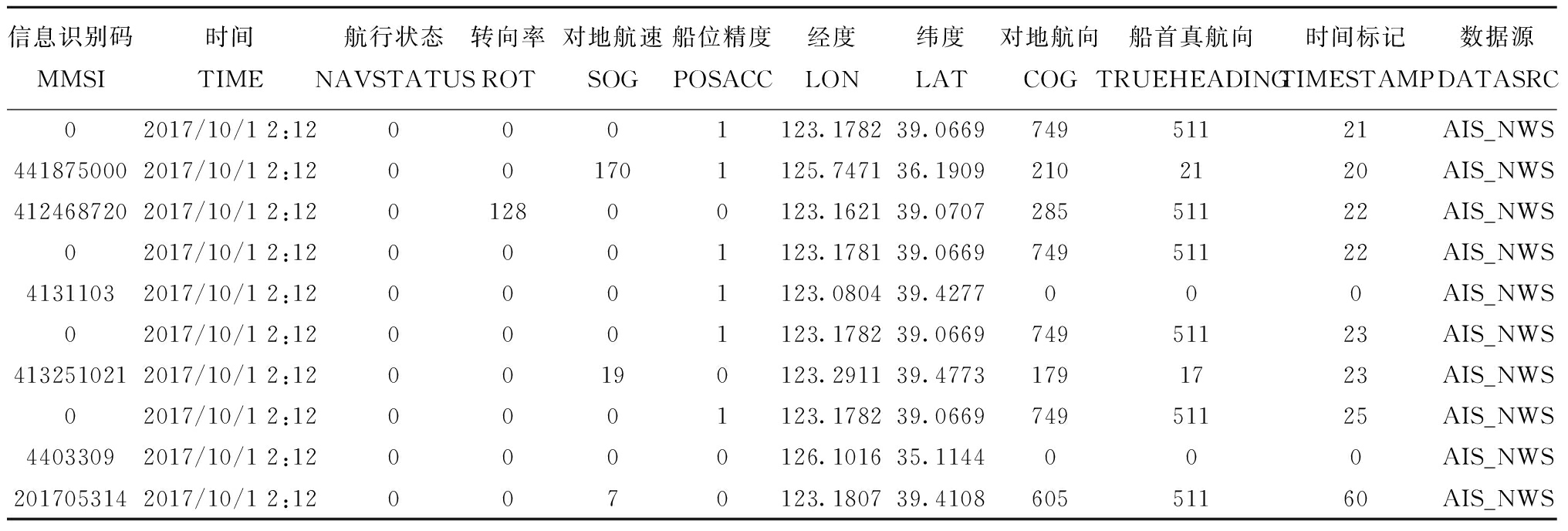
信息识别码MMSI时间TIME航行状态NAVSTATUS转向率ROT对地航速SOG船位精度POSACC经度LON纬度LAT对地航向COG船首真航向TRUEHEADING时间标记TIMESTAMP数据源DATASRC02017/10/1 2:120001123.178239.066974951121AIS_NWS4418750002017/10/1 2:12001701125.747136.19092102120AIS_NWS4124687202017/10/1 2:12012800123.162139.070728551122AIS_NWS02017/10/1 2:120001123.178139.066974951122AIS_NWS41311032017/10/1 2:120001123.080439.4277000AIS_NWS02017/10/1 2:120001123.178239.066974951123AIS_NWS4132510212017/10/1 2:1200190123.291139.47731791723AIS_NWS02017/10/1 2:120001123.178239.066974951125AIS_NWS44033092017/10/1 2:120000126.101635.1144000AIS_NWS2017053142017/10/1 2:120070123.180739.410860551160AIS_NWS
原始渔船数据未经过预处理,可能会因为AIS信号不稳等问题出现轨迹点漂移或缺失的情况,使轨迹的位置信息与实际不符,影响轨迹压缩效果,为此首先对出现以上情况的异常数据进行清洗。
若发生信号漂移的情况,若漂移点与前一点及漂移点与后一点的时间间隔小但距离间隔较大,而漂移点前后两点之间的时间间隔小距离间隔正常,则剔除该漂移点。
若发生信号丢失的情况,则通过缺失点前后两个已知的数据点对缺失部分进行线性拟合,如图4所示。
设缺失的数据点为(xi,yi,ti),前后两个已知点为(xi-1,yi-1,ti-1)和(xi+1,yi+1,ti+1),通过这两个已知的数据来拟合点(xi,yi,ti),填补缺失值。拟合公式如下:
(xi, yi)=(xi+1, yi+1)+[(xi+1,yi+1)-
(xi-1, yi-1)]/(ti+1-ti-1)×(ti-ti-1)。
(10)
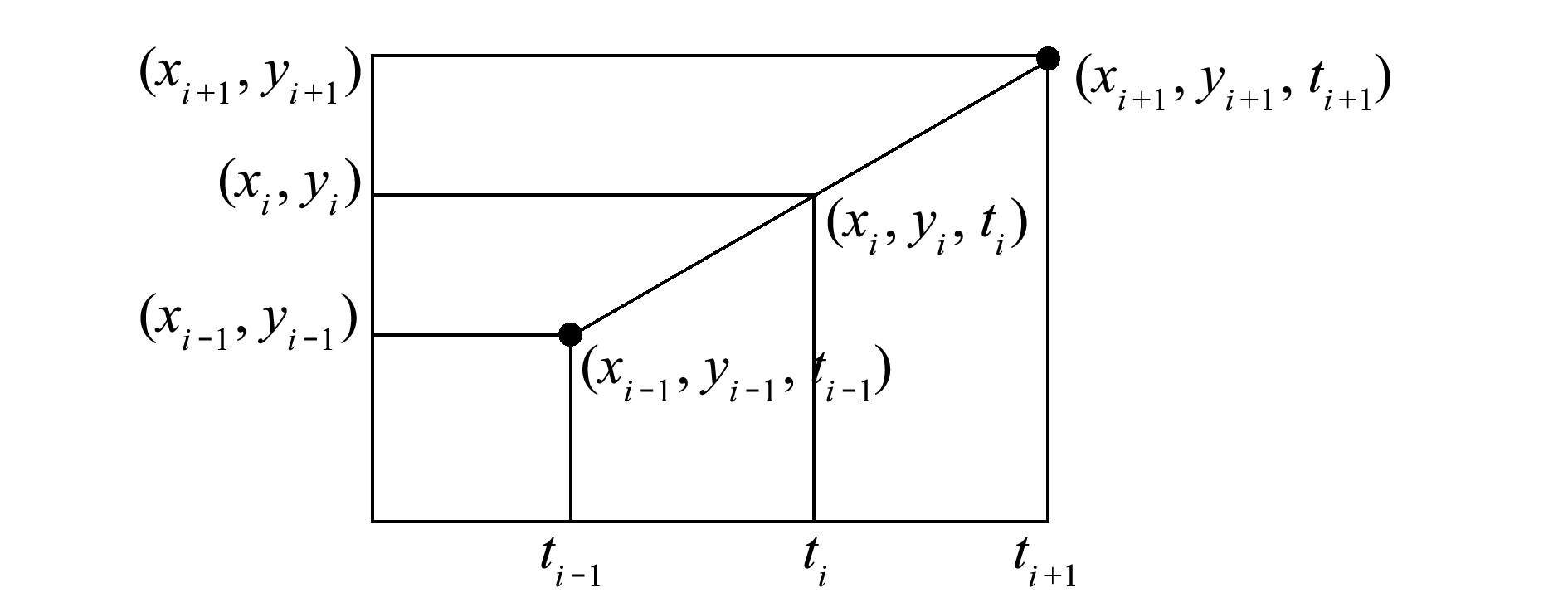
图4 线性拟合示意图
Fig.4 Schematic diagram of linear fitting
将数据进行预处理后,从库中抽取一条船连续6 d的运行轨迹,从数据库中选取的渔船唯一识别号(MMSI)为42424242,时间为10月1日至6日,按照时序整理提取渔船信息,包含航行状态、精度、对地航速、经度、纬度,如表4所示。
本文选用Sliding Window算法和D-P算法作为对比算法,以压缩效率作为试验结果参考,对3种算法进行评测,评测公式如下:
R=1-N/M×100%。
(11)
表4 整理后的轨迹数据样例
Tab.4 Samples of the processed trajectory data
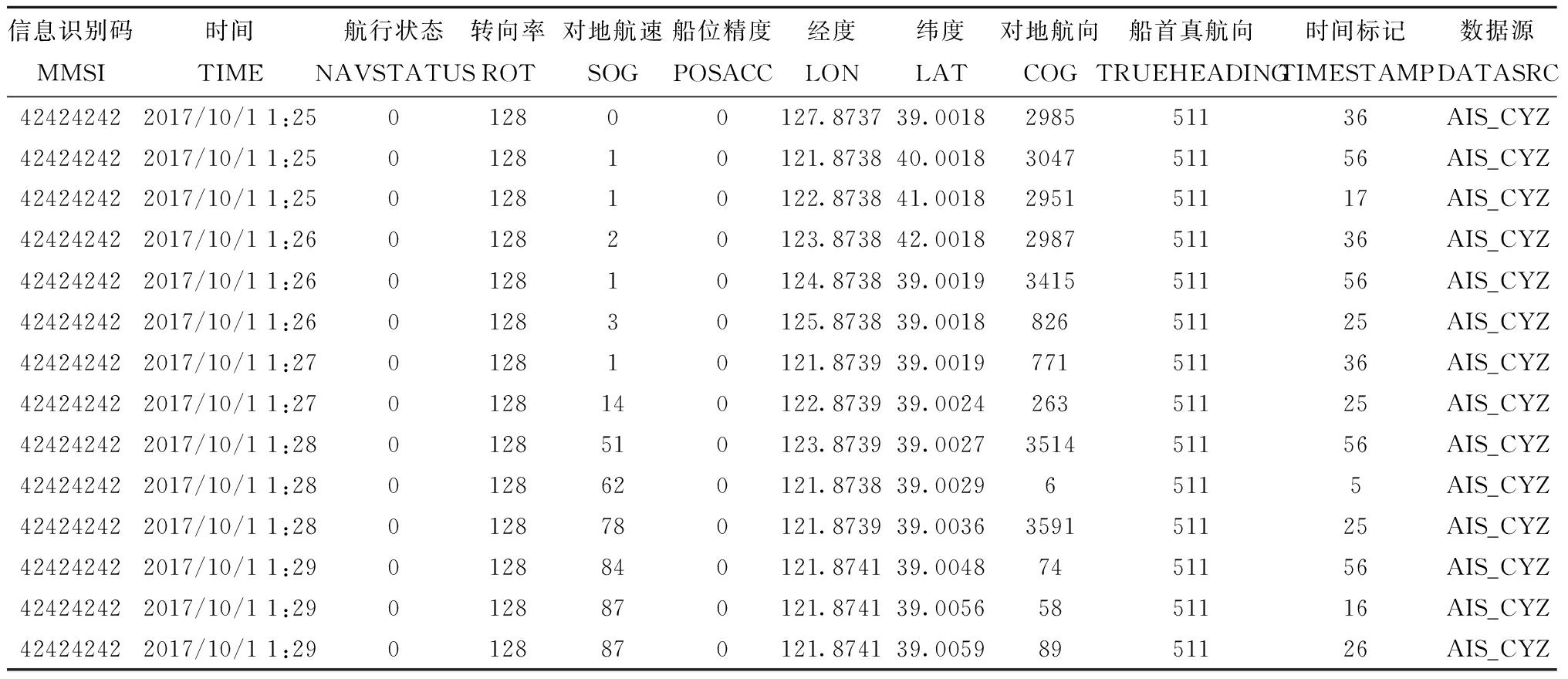
信息识别码MMSI时间TIME航行状态NAVSTATUS转向率ROT对地航速SOG船位精度POSACC经度LON纬度LAT对地航向COG船首真航向TRUEHEADING时间标记TIMESTAMP数据源DATASRC424242422017/10/1 1:25012800127.873739.0018298551136AIS_CYZ424242422017/10/1 1:25012810121.873840.0018304751156AIS_CYZ424242422017/10/1 1:25012810122.873841.0018295151117AIS_CYZ424242422017/10/1 1:26012820123.873842.0018298751136AIS_CYZ424242422017/10/1 1:26012810124.873839.0019341551156AIS_CYZ424242422017/10/1 1:26012830125.873839.001882651125AIS_CYZ424242422017/10/1 1:27012810121.873939.001977151136AIS_CYZ424242422017/10/1 1:270128140122.873939.002426351125AIS_CYZ424242422017/10/1 1:280128510123.873939.0027351451156AIS_CYZ424242422017/10/1 1:280128620121.873839.002965115AIS_CYZ424242422017/10/1 1:280128780121.873939.0036359151125AIS_CYZ424242422017/10/1 1:290128840121.874139.00487451156AIS_CYZ424242422017/10/1 1:290128870121.874139.00565851116AIS_CYZ424242422017/10/1 1:290128870121.874139.00598951126AIS_CYZ
其中:R为压缩率;M为压缩前轨迹点的个数;N为压缩后的轨迹点的个数。
3.2 试验结果
从图5可见:3种算法对渔船轨迹进行压缩后,原始轨迹点都大幅度减少,但当数据中出现折返路径,即渔船在捕捞区域作业的情况下,D-P算法虽然能够保留轨迹形态(图5-A2、B2),但压缩掉大量的有用信息;Sliding Window算法在轨迹点密集的地方出现轨迹丢失的现象(图5-A3、B3),压缩后的轨迹存在较大误差;相比D-P算法而言,基于改进滑动窗口的渔船轨迹压缩算法能够更好地保留渔船作业时的轨迹点(图5-A4、B4),能够较好地保留3轨迹的形状特征。
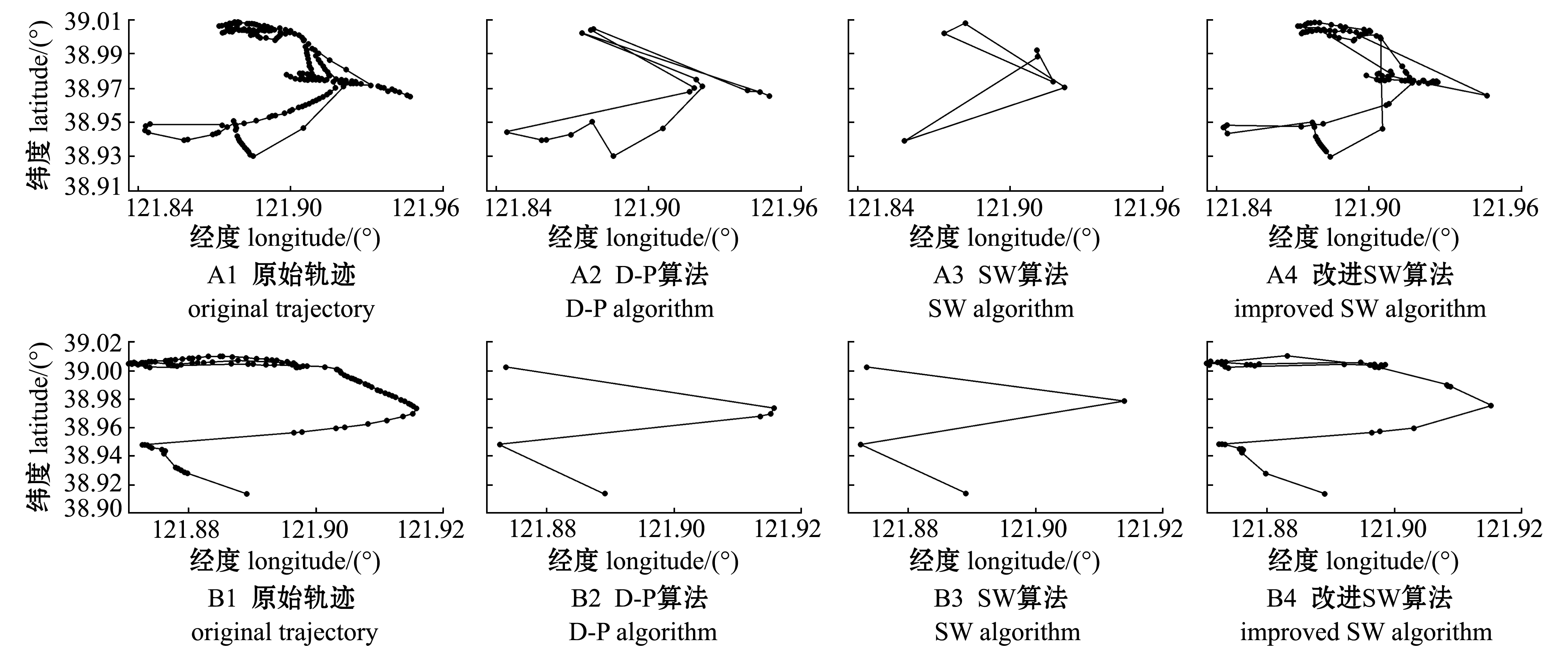
图5 渔船轨迹压缩前(A)后(B)效果对比图
Fig.5 Results of fishing vessel trajectory before(A) and after(B) compression
算法运算结果如表5所示,3种算法中SW算法的压缩率最高,6 d的数据压缩率平均在99.6%以上,其次是D-P算法,压缩率在99.3%左右,而改进的滑动窗口压缩算法的压缩率控制在94%以下,保留了更多的渔船轨迹特征点,更有利于后续的渔船作业行为分析工作。
表5 3种压缩算法的试验结果
Tab.5 Experimental results of three compression algorithms
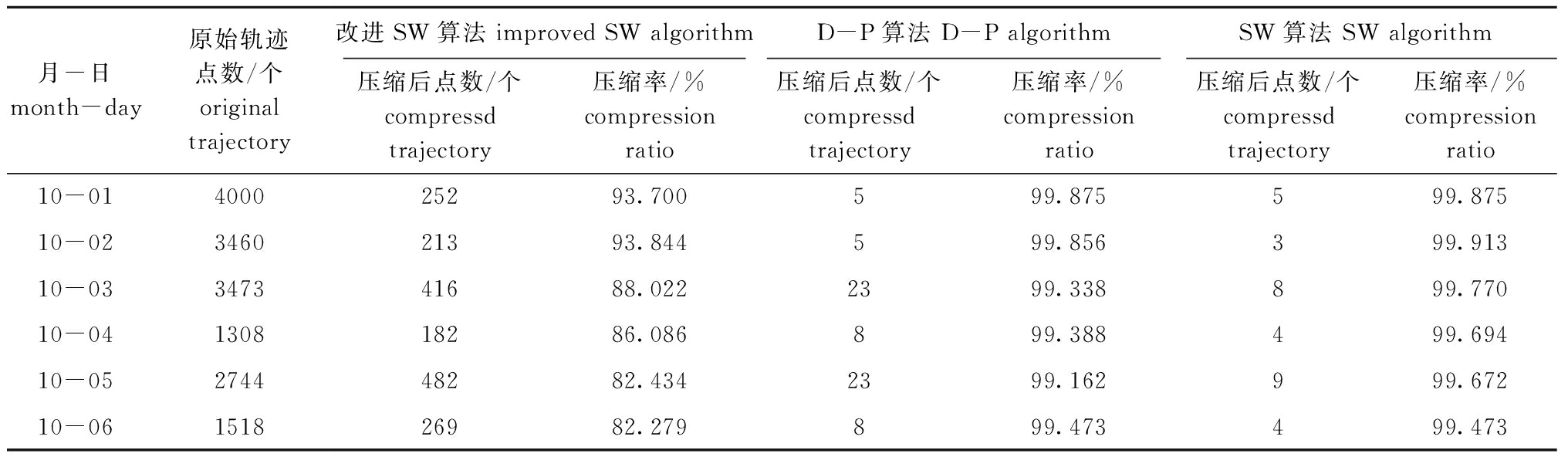
月-日month-day原始轨迹点数/个original trajectory改进SW算法 improved SW algorithmD-P算法 D-P algorithmSW算法 SW algorithm压缩后点数/个compressd trajectory压缩率/%compression ratio压缩后点数/个compressd trajectory压缩率/%compression ratio压缩后点数/个compressd trajectory压缩率/%compression ratio10-01400025293.700599.875599.87510-02346021393.844599.856399.91310-03347341688.0222399.338899.77010-04130818286.086899.388499.69410-05274448282.4342399.162999.67210-06151826982.279899.473499.473
4 结论
针对现有轨迹压缩算法在渔船轨迹数据方面存在压缩率太高导致特征点丢失等问题,提出一种改进的滑动窗口压缩算法。通过对比试验证明,D-P算法应用于渔船轨迹压缩工作时,由于压缩率高而导致特征点大量丢失,压缩误差较大,文中提出的基于改进滑动窗口的压缩算法虽然压缩率有所降低,但能够保留大量特征点,而且压缩后得到的轨迹与原始轨迹相似度更高,具有一定的研究价值,对于如何进一步减少压缩误差,将在未来继续研究。
致谢:感谢大连世想海洋科技有限公司提供数据支撑!
[1] 陶冶,奚海波,王建彬,等.近海玻璃钢拖网渔船的技术经济方程和特征分析[J].大连海洋大学学报,2015,30(3):330-333.
[2] 魏照坤,周康,魏明,等.基于AIS数据的船舶运动模式识别与应用[J].上海海事大学学报,2016,37(2):17-22.
[3] 张胜茂,程田飞,王晓璇,等.基于北斗卫星船位数据提取拖网航次方法研究[J].上海海洋大学学报,2016,25(1):138-144.
[4] 温国平,于晓利.渔业船舶事故类型的灰色关联分析[J].大连海洋大学学报,2017,32(2):237-241.
[5] 胡波华.AIS在渔船上应用有关问题的探讨[J].中国水运(下半月),2013(6):66-67,69.
[6] 齐乐,郑中义,李国平.互见中基于AIS数据的船舶领域[J].大连海事大学学报,2011,37(1):48-50.
[7] 盛凯,刘忠,周德超,等.基于运动模式的船舶轨迹分段压缩算法[J].海军工程大学学报,2018,30(6):50-57.
[8] 潘家财,姜青山,邵哲平.船舶会遇的时空数据挖掘算法及应用[J].中国航海,2010,33(4):57-60,64.
[9] 任亚磊.基于AIS数据的船舶会遇特征研究[D].武汉:武汉理工大学,2013.
[10] 刘虎,李伟峰.基于AIS数据的海上交通流区域自动识别[J].中国航海,2016,39(4):87-90,132.
[11] De Vries G K D,Van Someren M.Machine learning for vessel trajectories using compression,alignments and domain knowledge[J].Expert Systems with Applications,2012,39(18):13426-13439.
[12] 丁振国.船舶AIS数据云存储系统研究[J].浙江交通职业技术学院学报,2016,17(1):37-42.
[13] 江俊文,王晓玲.轨迹数据压缩综述[J].华东师范大学学报:自然科学版,2015(5):61-76.
[14] Douglas D H,Peucker T K.Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J].Cartographica,1973,10(2):112-122.
[15] 李名,胡勤友,孟良.基于AIS的船舶运动轨迹压缩技术研究[J].航海技术,2010(1):11-13.
[16] 张树凯,刘正江,张显库,等.基于Douglas-Peucker算法的船舶AIS航迹数据压缩[J].哈尔滨工程大学学报,2015,36(5):595-599.
[17] 徐凯,邱家瑜,李燕.一种加入时间维的船舶轨迹高效离线压缩算法研究[J].计算机科学,2017,44(11A):498-502.
[18] 张达夫,张昕明.基于时空特性的GPS轨迹数据压缩算法[J].交通信息与安全,2013,31(3):6-9.
[19] Keogh E,Chu S,Hart D,et al.An online algorithm for segmenting time series[C]//Proceedings of 2001 IEEE International Conference on Data Mining.San Jose,USA:IEEE,2001.
[20] 高邈,史国友,李伟峰.改进的Sliding Window在线船舶AIS轨迹数据压缩算法[J].交通运输工程学报,2018,18(3):218-227.
[21] 宋鑫,朱宗良,高银萍,等.动态阈值结合全局优化的船舶AIS轨迹在线压缩算法[J].计算机科学,2019,46(7):333-338.
[22] de Amorim R C,Mirkin B.Selecting the minkowski exponent for intelligent k-means with feature weighting[M]//Aleskerov F,Goldengorin B,Pardalos P M.Clusters,Orders,and Trees:Methods and Applications.New York:Springer,2014.
[23] 刘敦伟.基于AIS数据的船舶航线挖掘[D].大连:大连海事大学,2017.
[24] 胡江强,杨盐生,李铁山.恒向线航向和航程的精确计算[J].大连海事大学学报,2005,31(2):11-14.
[25] Cao Xin,Cong Gao,Jensen C S.Miningsignificant semantic locations from GPS data[J].Proceedings of the VLDB Endowment,2010,3(1-2):1009-1020.