循环水养殖系统中养殖池的合理设计是实现鱼类最佳养殖条件、水循环再利用及减少环境污染的关键环节[1-3],方形养殖池和圆形养殖池是循环水养殖系统中常用的两种养殖池几何结构型式。方形养殖池主要优点是空间利用率大、操作方便,但由于直角对养殖池内流速、水力混合均有不利影响,导致产生较大面积低流速区及死区容积,不利于积聚在池底的残饵粪便等固体废弃物的排污。而残留在池底的固体废弃物增加了生化需氧量,使溶解氧产生较大梯度,进而导致鱼类分布和鱼类质量的差异[4]。圆形养殖池的自清洁特性是基于一种被称为“茶杯效应”的现象,旋转的水体沿容器底部产生二次径向流,将沉淀的颗粒引至底部中心,若排水口位于池底中心,则固体废弃物可以快速地从养殖池底部中心排水口排出[5]。
养殖池作为循环水养殖系统的重要组成部分,对鱼类的健康高效生长发挥着重要作用,目前,试验方法与数值模拟方法已被广泛应用于研究养殖池系统的水动力及相关特性,从养殖池几何形状优化和进出水装置改进等多方面开展研究[6]以改善养殖池系统的水动力特性和集排污性能。已有学者采用试验方法进行养殖池的垂直挡板设置以改善流场及排污效果,垂直于水流安置的挡板可增加底部流速,并减少固体废弃物的堆积,但设置的垂直挡板对高密度养殖鱼类形成了干扰[7-10]。Watten等[11]对进水装置进行了改进试验,在垂向进水系统的基础上,沿养殖池底部单侧增设了进水管并沿着养殖池底部射流,改善了养殖池的自清洁性能,但增加了进水系统的复杂性和管理操作的难度。
随着数值模拟技术的不断发展和相关理论的完善,数值模拟的作用日益凸显[12],计算流体力学技术(CFD)也逐渐被应用于流场特征、集排污、生物滤器等研究[13-15]。与试验方法相比,数值模拟方法能获取更丰富的养殖池系统流场信息,易于改变养殖池模型结构参数,从而进行结构优化[16-17]。Liu等[18]对循环水八角形养殖池进行了数值模拟研究,并指出CFD数值结果对揭示循环水养殖系统内部流体动力学特征及其参数的优化具有重要意义;魏武[19]对圆形养殖池内流场进行了数值模拟,指出可借助CFD技术为圆形养殖池的优化和运行管理提供依据。为了将圆形养殖池的水动力优势与方形养殖池的空间利用率高、操作方便的优点相结合。本研究中,采用圆弧角代替直角的方式优化方形养殖池以改善养殖池的水动力及相关特性,并基于CFD技术建立三维湍流数值计算模型,对不同圆弧角尺度的单通道方形养殖池流场特性进行研究,并基于养殖池流场特性对养殖池类型进行定义,依据不同圆弧角尺度对养殖池流场特性的影响将养殖池划分为方形养殖池、近方形养殖池、方形圆弧角养殖池、近圆形养殖池和圆形养殖池,旨在为方形圆弧角养殖池的建设提供理论和设计依据。
1 数值模型
1.1 控制方程
湍流是普遍存在的流体运动,养殖池水动力研究中边界层效应不可忽略,建立湍流模型是养殖池水动力特性研究的重要基础。RNG k-ε模型和标准k-ε模型是养殖池水动力研究中常用的两种湍流模型。RNG k-ε模型是对标准k-ε模型的改进,它考虑了平均流动中的旋转和旋流流动情况,并在ε方程中反映了主流的时均应变率。与标准k-ε模型相比,RNG k-ε模型可以更好地处理高应变率及流线弯曲程度较大的流动[20]。因此,本研究中湍流模型选用RNG k-ε模型,固体壁面采用标准壁面函数,压力速度耦合方式采用SIMPLE的方法,湍流动能采用一阶迎风离散模式。
1.2 水动力学分析特征量
Tvinnreim[21]针对带有中央出口的养殖池开展研究,指出通过改变入口的冲力Fi(N),可以优化池内的速度和流场分布。Fi计算公式为
Fi=ρQ(vin-vavg)。
(1)
其中:ρ为水的密度(kg/m3);Q为进水流量(m3/s);vin为进水速度(m/s);vavg为养殖池内平均速度(m/s)。
Oca等[22]针对具有多个涡流的矩形养殖池开展研究,养殖系统在稳态运行条件下,养殖池阻力Ft消耗的功率Pt等于入口冲力Fi提供的功率Pi。因此,Oca等[22]定义了养殖池内阻力系数Ct,其计算公式为
(2)
其中:A为湿周(m2),养殖池壁面与水接触的面积。
Masaló等[23]定义了用均匀系数(DU50)分析养殖池水流速度均匀性,即50%的较低水流速度的平均值v50(m/s)和平均速度v0(m/s)的比值,即
DU50=v50/v0×100。
(3)
其中:平均速度v0(m/s)通过半径加权来获得,即
v0=∑viri/∑ri。
(4)
式中:vi为径向位置为ri(m)时的速度(m/s)。
2 模型验证
为验证数值模型建立的正确性和模拟结果的精度,本研究中与Davidson等[24]的Cornell-type双通道养殖池结构试验结果进行了比较,并依据Davidson等[24]的试验模型参数进行建模与网格划分。
验证模型设计参数:圆形养殖池直径为3.66 m,水深为0.91 m,底部出流口直径为0.05 m,溢流口直径为0.15 m,进水口直径为0.042 m。如图1所示,边壁设6个进水口,从上到下前4个进水口设向左45°弯头,第5个进水口设向下45°弯头,第6个(最下侧)进水口不设置弯头。
模型以四面体网格进行划分,对进水口、底流口、溢流口位置进行了加密处理,网格混合单元总数约为147万个。Cornell-type双通道养殖池模型和网格划分示意图如图1所示。
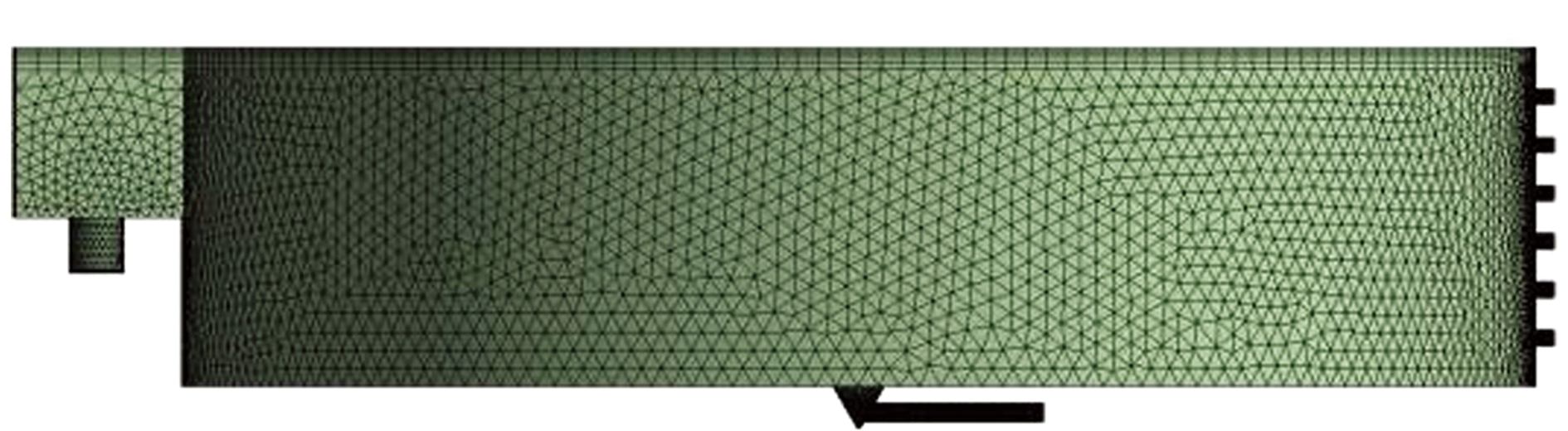
图1 Cornell-type双通道养殖池网格划分示意图
Fig.1 Schematic of meshing diagram of a Cornell-type dual-drain culture tank
数值模拟计算基于计算流体力学技术中Fluent模块,边界条件设置如下。
入口边界:速度入口,入口速度设为1 m/s,湍流强度设为4.25%,水力直径为0.042 m。
出口边界:自由出流。
固体壁面边界:养殖池池底和池壁均为固体壁面。
自由边界条件:水表面按自由面处理,压力值为大气压。
参照Davidson等[24]设置一个通过池中心的纵切面,其中一端位于进水口后380 mm处,且水流从进水口流出,先经过的点位于正半轴,在不同深度5个横截面距池底分别为0.06、0.212、0.364、0.516、0.668 m)进行速度监测,将不同深度相同位置监测值取平均值作为养殖池内相应径向位置速度的代表值。数值计算与试验结果对比见图2。
图2显示,养殖池中心速度的试验结果高于数值模拟结果,主要是因为养殖池中心存在涡流导致试验结果较大。试验结果与模拟结果对比中,绝大多数监测点的相对误差在10%以内,仅有个别点相对误差较大,总体来说,试验与模拟结果的平均相对误差在30%以内,数值模拟计算结果与试验结果吻合较好,主要监测位置数值模拟结果与试验结果比较接近。这表明本研究中建立的数值模型合理,精度基本满足要求,可用于养殖池水动力特性研究。
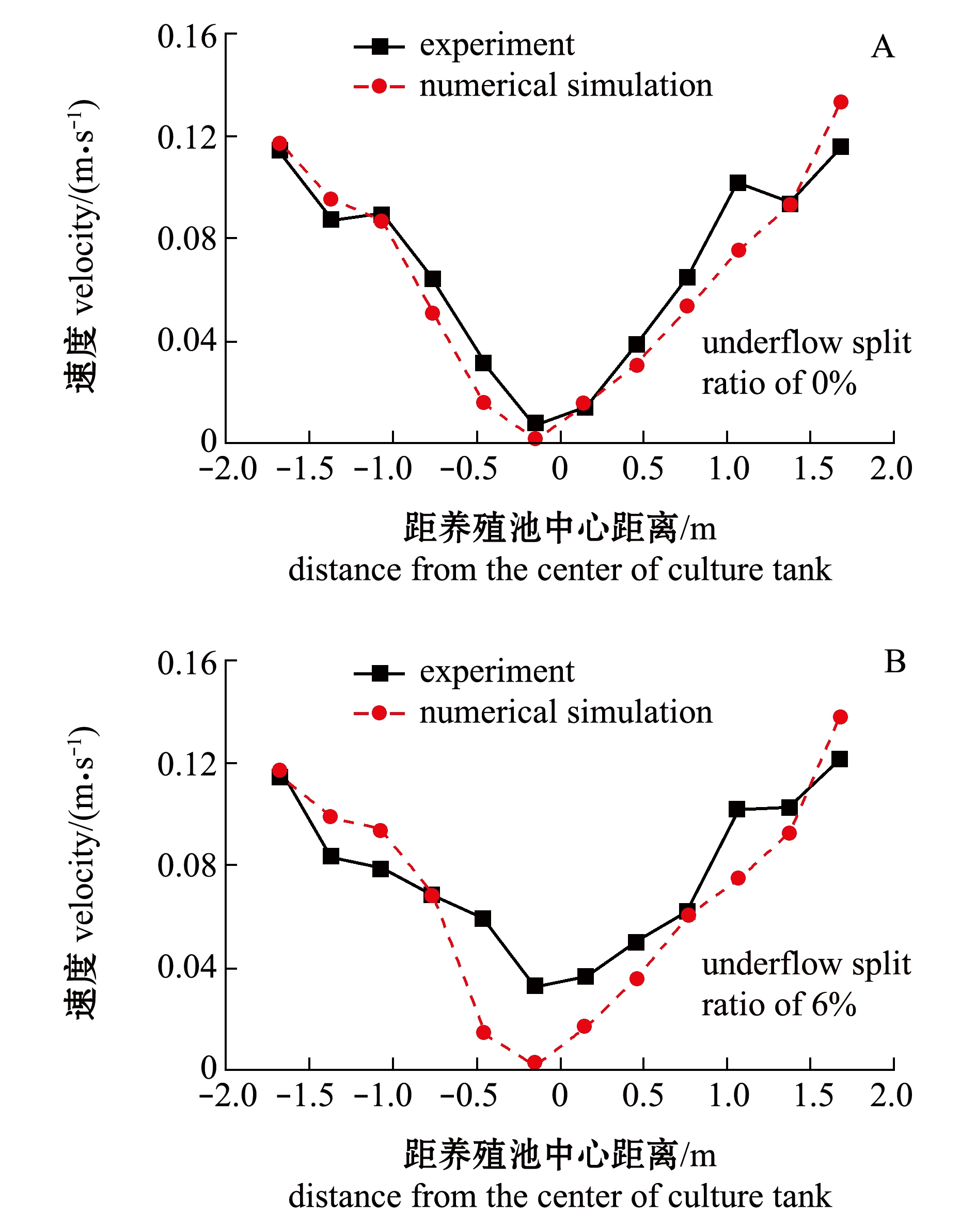
图2 不同底流分流比流速对比图
Fig.2 Velocity comparison with different underflow split ratios
3 模型建立
本研究中以单管入流、单通道出流的方形养殖池为研究对象,模型参数依据现有循环水养殖池系统进行同比例缩放并对部分参数进行优化,模型设计参数如下。
模型的长(L)×宽(B)为1 m×1 m(长宽比L/B=1∶1),水深(H)为0.2 m(径深比B/H=5∶1),池底部中心排污口内径为0.02 m,进水管直径为0.02 m。进水系统为单管射流驱动,进水管设置在养殖池直边壁的中间位置,垂直紧贴养殖池边壁(进水孔距池壁0.01 m),进水系统沿切向入流(射流方向与养殖池壁成0°夹角)。进水管自上而下均匀开18个孔,进水系统射流速度恒定为1 m/s,根据进水流量将孔径设置为3个组次(孔径记为d,进水流量记为Q):
(1)d=0.002 8 m,Q=400 L/h(循环次数约为50次/d);
(2)d=0.004 m,Q=814 L/h(循环次数约为100次/d);
(3)d=0.004 8 m,Q=1174 L/h(循环次数约为150次/d)。
本研究中以四面体网格对数值计算模型进行划分,在进水孔、排水口位置进行加密处理。以圆弧角半径与池体宽度之比(R/B)为0.25为例,模型和网格划分示意图如图3所示。

图3 单通道方形养殖池模型和网格划分示意图
Fig.3 Schematic model and meshing diagram of a single channel square culture tank
数值模拟计算基于计算流体力学技术中Fluent模块,边界条件设置如下。
入口边界:速度入口,入口速度设置为1 m/s,流速均匀分布,湍流强度和水力直径根据进水流量设置为3个组次,当Q=400 L/h时,湍流强度设置为6%,水力直径为0.002 8 m;当Q=814 L/h时,湍流强度设置为5.7%,水力直径为0.004 m;当Q=1174 L/h时,湍流强度设置为5.57%,水力直径为0.004 8 m。
出口边界:压力出口。
固体壁面边界:养殖池池底和池壁均为固体壁面。
自由边界条件:水表面按自由面处理,压力值为大气压。
4 结果与讨论
4.1 相对弧宽比对养殖池流速特征的影响
本研究中对采用不同尺度圆弧角代替直角的方形养殖池进行数值模拟计算,不同R/B工况下的养殖池内平均流速如图4所示。结果显示:3个进水流量工况下的养殖池内平均流速均随着R/B的增大而增大,而且进水流量越大平均流速上升的趋势越明显;当0.2≤R/B<0.4时,随着R/B的增大平均流速呈现平缓上升趋势,而0≤R/B<0.2和0.4≤R/B<0.5时,随着R/B增大平均流速呈现较快增长趋势。
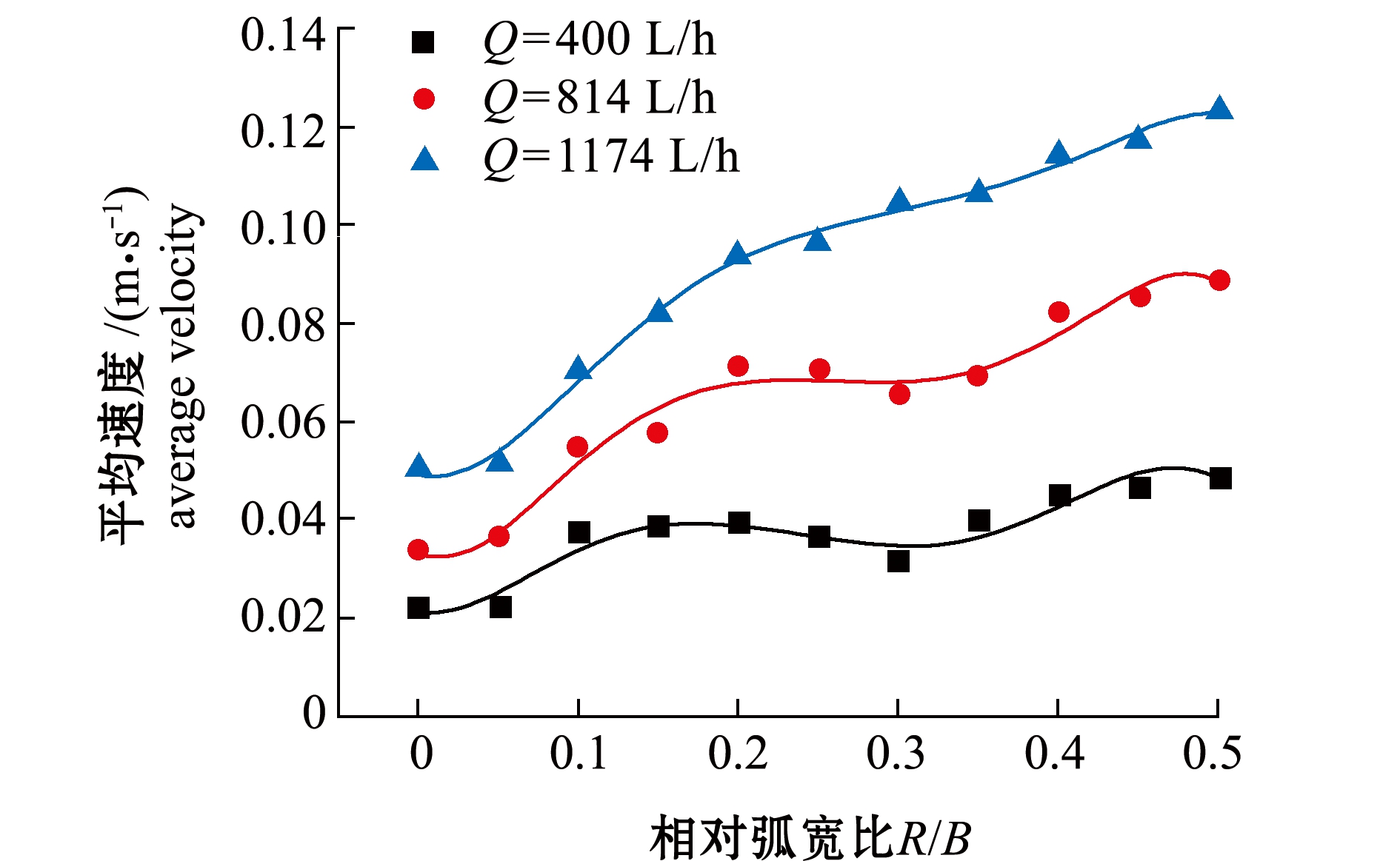
图4 不同进水流量工况下养殖池内平均流速随R/B的变化趋势
Fig.4 Variation in average velocity with relative arc to width ratio(R/B)at different inlet flow rates
当R/B为0(方形养殖池)时,相邻池壁通过直角过渡衔接,当水体流经直角处时需要急剧转向,水体与池壁产生剧烈碰撞及折射、反射,此过程伴随较大的能量损失,碰撞等水体与池壁间的剧烈相互作用产生的能量损失是主要因素,与池壁间的摩擦耗能是次要因素。随着圆弧角的增大,碰撞的程度逐渐减小,产生的能量损失也逐渐减小,致使流速呈现上升的趋势。随着R/B(0<R/B<0.2)的增大,水体与池壁产生碰撞及折射、反射的剧烈程度趋于减弱,伴随的能量损失也逐步减小,养殖池内平均流速呈现上升的趋势。当R/B增大到0.2时,圆弧角尺度起到明显改善水体与转角处的激烈相互作用,引导水流从池体一侧直壁沿圆弧角平滑过渡到另一侧直壁,水体与池壁间的能量损失主要由与池壁间的摩擦造成,碰撞等消耗起次要作用。当0.2≤R/B<0.4时,养殖池流场特性呈现相对稳定状态,平均流速呈现平缓上升趋势。当0.4≤R/B<0.5时,整个养殖池壁4个角主要由弧壁和小段直壁组成,水体沿池壁行进及转向均基本能顺畅完成,水体与池壁产生碰撞及折射、反射的剧烈程度较小,伴随的能量损耗也较少,摩擦造成的能量损失也随池壁周长的减小而逐渐减小,养殖池内流速又呈现明显上升的趋势。当R/B为0.5(圆形养殖池)时,养殖池壁均为圆弧构成,水体沿池壁稳定行进过程伴随最小的能量损耗,此时养殖池内平均速度最高。
养殖池内水体平均速度监测曲线如图5所示,随着R/B增大,平均速度监测曲线从不规则状态到有节律震荡,最终平均速度监测曲线趋于稳定。随着R/B增大,水体与池壁产生剧烈碰撞及折射、反射等不稳定因素程度减弱,能量消耗减小,因而监测的平均速度稳定性逐渐改善,平均速度增大。
养殖池中间截面(距池底0.1 m)的平均速度监测曲线如图6所示,随着进水流量增大,平均速度监测曲线更加稳定。因为输入养殖池系统的能量主要用于养殖池系统的阻力消耗和克服水体质点间相对运动的阻力消耗,进而维持养殖池系统水体运动。在进水流量较低(400 L/h)的工况下,抵抗养殖池系统阻力消耗占输入能量比率较高,进而抵抗水体质点间相对运动的阻力损耗比率较低,养殖池系统水体整体混合不充分,平均速度监测曲线稳定性较差;而进水流量较高(1174 L/h)的工况则呈现相反的趋势,抵抗水体质点间相对运动的阻力消耗比率较高,养殖池系统水体整体混合充分均匀,平均速度监测曲线稳定性较好。
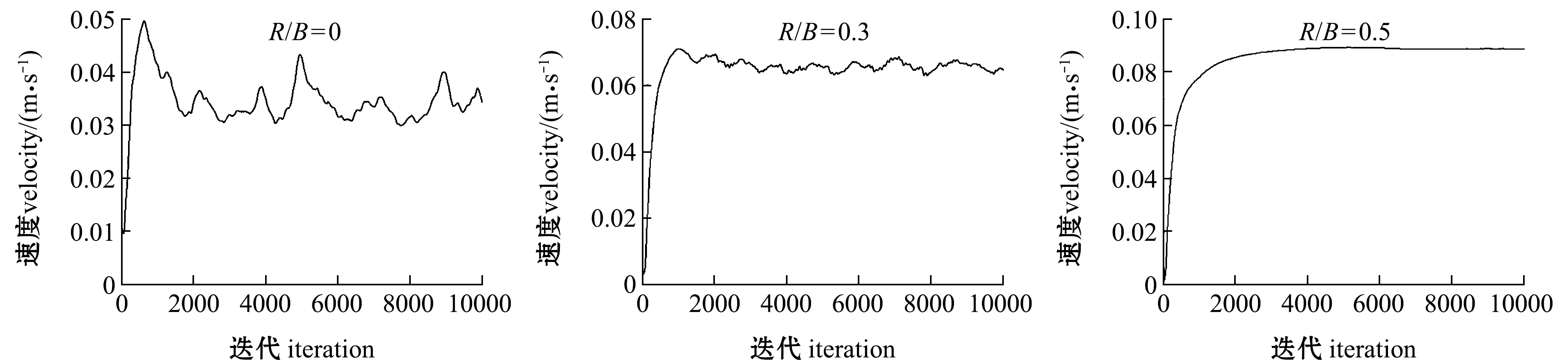
图5 不同R/B工况下池内水体平均速度监测曲线(Q=814 L/h)
Fig.5 Average velocity monitoring curve of waters in the tanks with different R/B values(Q=814 L/h)

图6 不同进水流量工况下池内中间截面平均速度监测曲线(R/B=0.25)
Fig.6 Average velocity monitoring curve of plane at different inlet flow rates(R/B=0.25)
4.2 相对弧宽比对速度均匀系数的影响
进水系统水平射流条件下,特定径向位置的切向速度基本上与其所处深度无关[25]。本研究中在养殖池中间截面(距池底0.1 m)设置72个监测点,以截面中心为圆心设9个间距为5 cm的圆周,每个圆周取的8个点分别位于养殖池的横纵轴线和两条对角线上。根据式(3)计算出的均匀系数如表1所示。
从表1可见,随着进水流量的增大养殖池流场均匀性明显改善,这是因为进水流量较高的工况提供克服水体质点间相对运动的摩擦阻力所消耗的能量比率较高,养殖池系统水体整体混合充分。随着R/B的增大,流场均匀性在不同进水流量工况下呈现不同的变化趋势,在进水流量小(400 L/h)的工况下,随着R/B的增大呈现两次递增和两次递减的双峰趋势;而在进水流量大(1174 L/h)的工况下,随着R/B的增大总体呈现先增大后减小的单个峰值趋势;中等进水流量(814 L/h)工况下,随着R/B的增大呈现双峰趋势向单峰趋势的过渡状态(表1)。这主要是因为养殖池存在环流运动和离心运动两种主要的运动状态,在这个过程中水体不断混合,当R/B较小或较大时池内水体主要呈现受池壁形状影响较大的环流运动状态,池内能量主要由克服养殖池系统阻力和水体质点间的相互碰撞等不利于水体运动所消耗的能量和克服水体质点间相对运动的摩擦阻力等有利于水体运动所消耗的能量组成,当R/B较小时,克服养殖池系统阻力消耗对池内水体运动特征影响显著,而当R/B较大时,克服水体质点间相对运动对池内水体运动起到主导作用。但R/B在中值区域的养殖池内水体呈现不同程度的离心运动状态,运动状态与克服养殖池系统阻力后的剩余能量密切相关。当有充足的能量使离心运动状态时的水体质点间相互碰撞所损耗的能量比率达到可以忽略的情况下,池内水体呈现有序运动状态,并表现出较高的混合均匀性;当能量不足以忽略此时较高的能量损耗比率时,邻近池壁的水体有强烈地向池中心运动混合趋势,这个过程伴随池内水体不同程度的无序运动与相互撞击,养殖池内的整体混合均匀性变差。
表1 不同进水流量工况下R/B对池内速度均匀系数的影响
Tab.1 Effect of R/B values on uniformity coefficient at different inlet flow rates

进水流量Q/(L·h-1)相对弧宽比relativearctowidthratio(R/B)00.050.100.150.200.250.300.350.400.450.504004058616452512650584341814415972637578626975666111746366757383818382807272
从图7可见:当R/B从0.2增大到0.3时,离心运动状态逐渐明显,邻近池壁的水体逐渐呈现明显地向池中心运动混合的趋势,水体质点间的不规则运动与相互撞击伴随着较大的能量消耗,导致养殖池中间区域出现大面积低流速区,池内水体混合均匀性逐渐变差;当R/B从0.3增大到0.4时,池内水体主要运动状态逐渐由离心运动变为受到池壁几何形状影响较大的环流运动,水体质点间的能量消耗比率减小,池内水体均匀性明显改善。此外,随着进水流量的增大,水体质点间的摩擦阻力能量消耗所占初始能量的比率增大,池内水体表现出较高的混合均匀性(图8)。
截取通过养殖池中心且不通过进水管的纵截面(y=0),其速度分布云图如图9所示,随着R/B增大,纵截面低流速区逐渐减少,高流速区逐渐增多,且当0.2≤R/B<0.4时,池内均匀性较好,这是因为水体与池壁碰撞而产生的能量损耗随着R/B增大而逐渐减小;而当0.4≤R/B<0.5时,池内水体受池壁形状影响较大,呈现较为规律的环流运动状态,能量损失较小,高流速区较多,流场均匀性并不优于0.2≤R/B<0.4时养殖池内流场均匀性。
4.3 相对弧宽比对养殖池阻力系数的影响
从图10可见:当进水流量较小时(Q=400 L/h),在R/B较小的情况下(0≤R/B<0.2),随着R/B增大,养殖池系统阻力系数呈递减趋势,原因是水体在转角位置与池壁发生强烈的碰撞进而造成较大的能量损失,碰撞程度会随着R/B的增大而明显减弱,能量损失也显著减小,水流与池壁间的运动阻力相应减小;当0.2≤R/B≤0.3时,随着R/B增大,养殖池系统阻力系数呈增大趋势,原因是在R/B增大过程中池内能量逐渐不足以忽略离心运动状态时水体质点间的相互撞击所产生的能量损耗,进而导致水体质点间的无序运动及相互撞击程度逐渐剧烈;当0.3<R/B≤0.5时,随着R/B增大,养殖池系统阻力系数又呈递减趋势,原因是养殖池水体质点间的撞击程度减弱,不规则无序运动逐步变为规则有序运动。
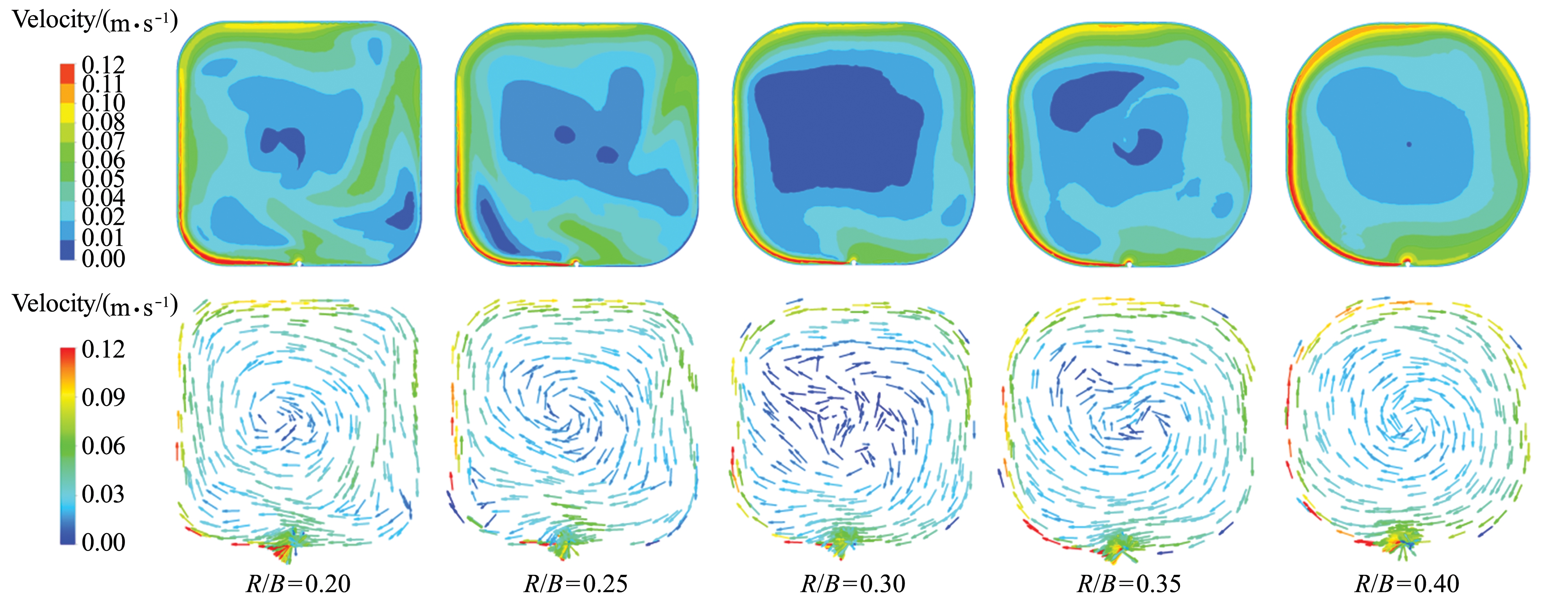
图7 不同R/B工况下池内横截面速度分布云图和速度矢量图(Q=400 L/h)
Fig.7 Contour maps and the vector maps of velocity magnitudes on the cross section at different R/B values(Q=400 L/h)
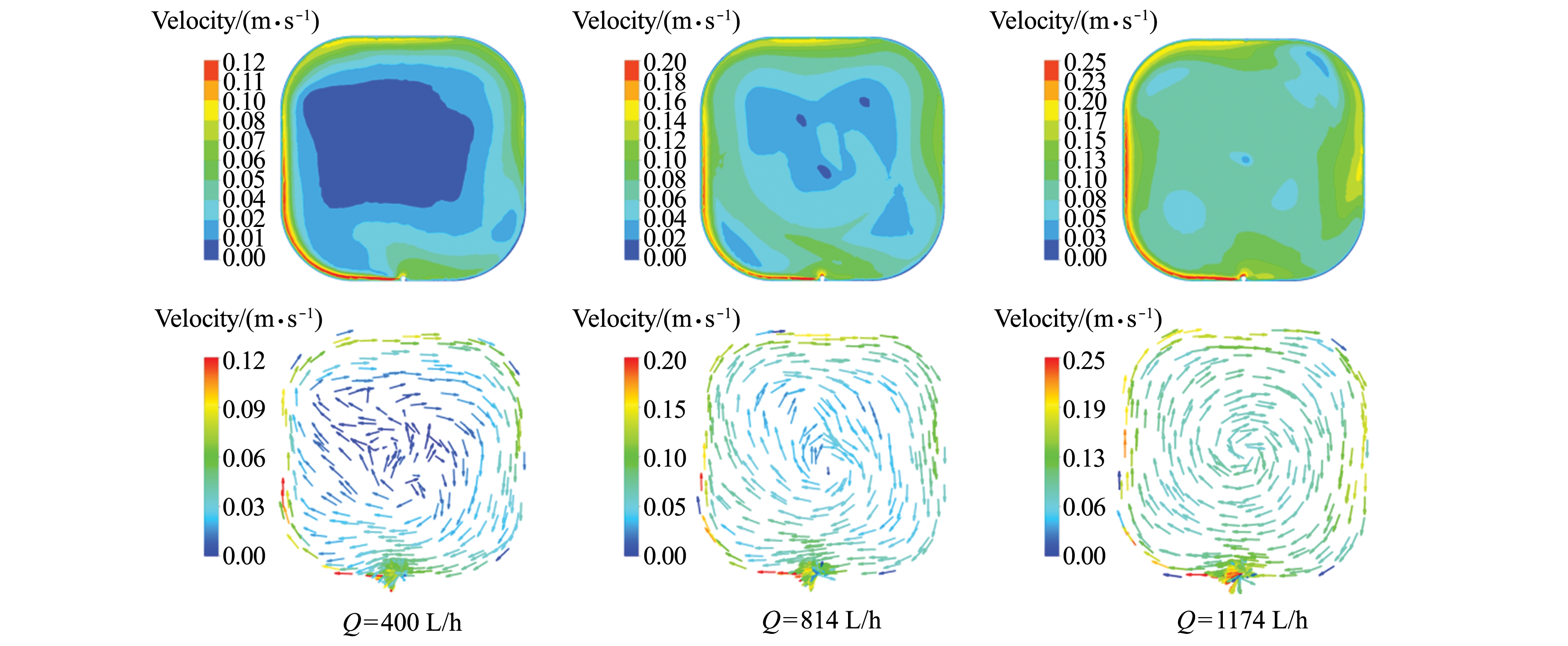
图8 不同进水流量工况下池内横截面速度分布云图和速度矢量图(R/B=0.3)
Fig.8 Contour maps and the vector maps of velocity magnitudes on the cross section at different inlet flow rates(R/B=0.3)

图9 不同纵截面速度分布云图(Q=1174 L/h)
Fig.9 Contour maps of velocity magnitudes on the longitudinal section(Q=1174 L/h)
从图10还可见:当进水流量较大时(Q=1174 L/h),随着R/B增大,养殖池系统阻力系数呈现单调递减规律,这是因为水体质点克服池壁摩擦的能量消耗比率逐渐降低,水体获得了较多的能量去维持环流运动和离心运动,池内能量足以忽略离心运动状态时水体质点间的相互撞击所产生的能量损耗,无论环流运动还是离心运动养殖池系统水体质点均呈现稳定有序状态;当进水流量处于中值区域时(Q=814 L/h),养殖池系统阻力系数变化规律呈现从低进水流量到高进水流量的过渡状态。
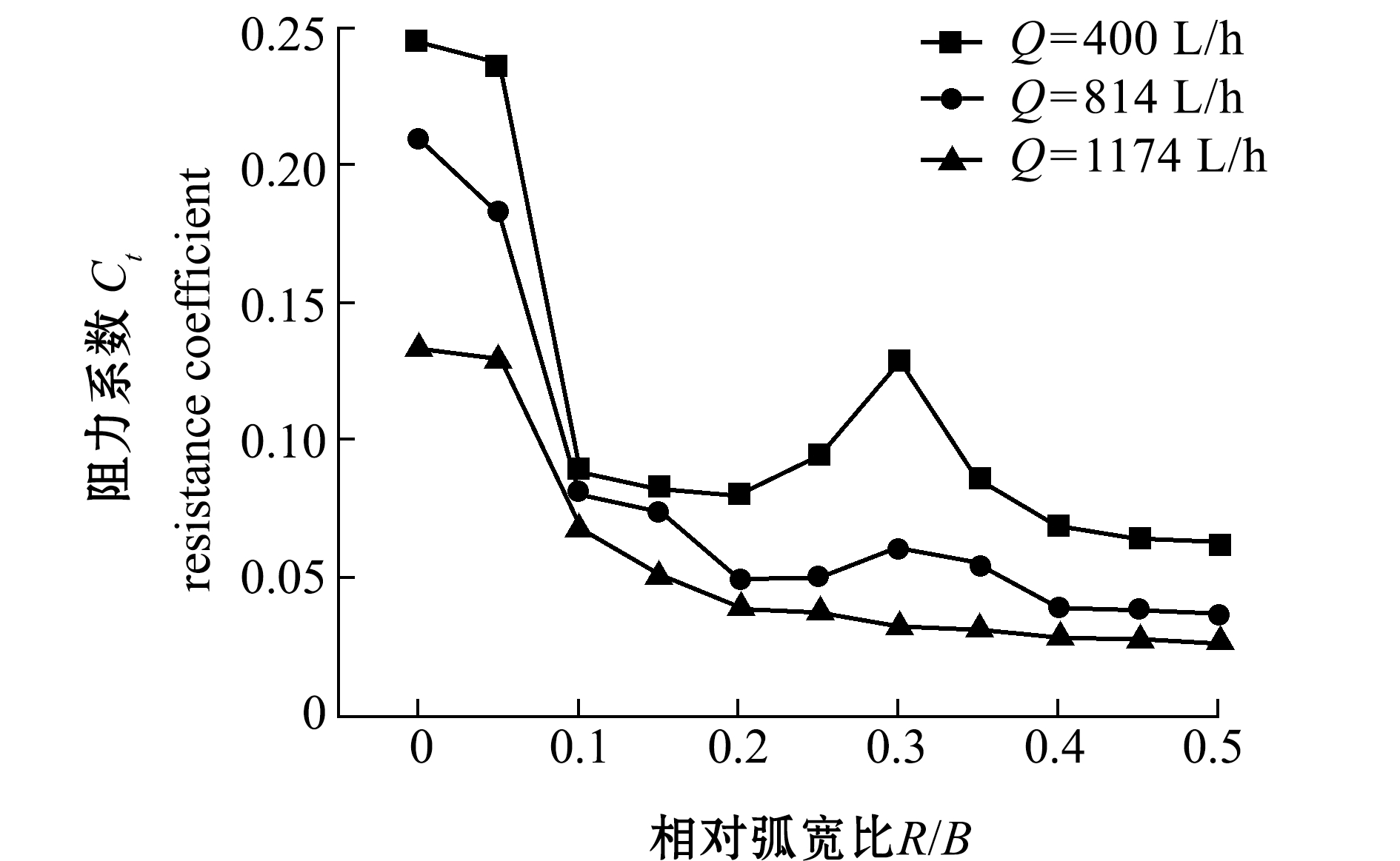
图10 不同进水流量时阻力系数随R/B的变化
Fig.10 Variation in resistance coefficient with R/B values at different inlet flow rates
4.4 养殖池池型分类
基于圆弧角优化的目的是开展不同R/B结构参数的水动力特性研究,并与相同结构尺度的方形和圆形养殖池水动力特征进行对比分析,获得显著区别于方形和圆形养殖池水动力特征的临界点结构参数,明确方形圆弧角养殖池定义。方形圆弧角养殖池可将圆形养殖池的水动力优势和方形养殖池的空间利用率高、操作方便的优点结合起来满足循环水养殖需求。养殖池空间利用率计算公式为
空间利用率=Sn/S0×100%。
(5)
其中:Sn为养殖池底面积,即有效养殖面积(m2);S0为R/B=0(方形养殖池)时的养殖面积(m2)。
本研究中依据养殖池流场特性将养殖池池型划分为方形养殖池、近方形养殖池、方形圆弧角养殖池、近圆形养殖池和圆形养殖池。其中,R/B=0为标准的方形养殖池,R/B=0.5为标准的圆形养殖池。由养殖池内平均流速、速度均匀系数、养殖池阻力系数和流场云图与矢量图综合分析得出,0<R/B<0.2的养殖池定义为近方形养殖池,0.2≤R/B<0.4的养殖池定义为方形圆弧角养殖池,0.4≤R/B<0.5的养殖池定义为近圆形养殖池。
如图11、图12所示,近方形养殖池空间利用率高达95%以上,但整体流速较低且流体质点运动是一种非平衡非规律状态,流场特征呈现随机状态,养殖池池水混合均匀性差;而方形圆弧角养殖池空间利用率相对于近方形养殖池略有减小,整体流速提高且流体质点运动趋于周期性震荡平衡的较规律状态,流场特征呈现一定规律性,其中R/B为0.20(空间利用率97%)和0.25(空间利用率95%)是兼具较好流场均匀性和高空间利用率的方形圆弧角养殖池,且池内均匀性较好;近圆形养殖池空间利用率较小,流体质点运动呈现稳定平衡的规则运动状态,整体流速较高且高低流速区分布稳定,但整体而言池水的混合均匀性并不优于方形圆弧角养殖池。

图11 养殖池空间利用率随R/B的变化
Fig.11 Variation in spatial utilization rate in the tank with R/B values
5 结论
本研究中建立了三维湍流数值计算模型并进行了验证,通过数值模拟计算研究了R/B对养殖池流场特性的影响,得到以下结论:
(1)模型验证结果显示,数值模拟计算结果与试验结果绝大多数监测点的相对误差在10%以内,吻合良好,证明了本研究中建立的数值模型的合理性,精度基本满足要求,可应用于养殖池水动力特性的研究。
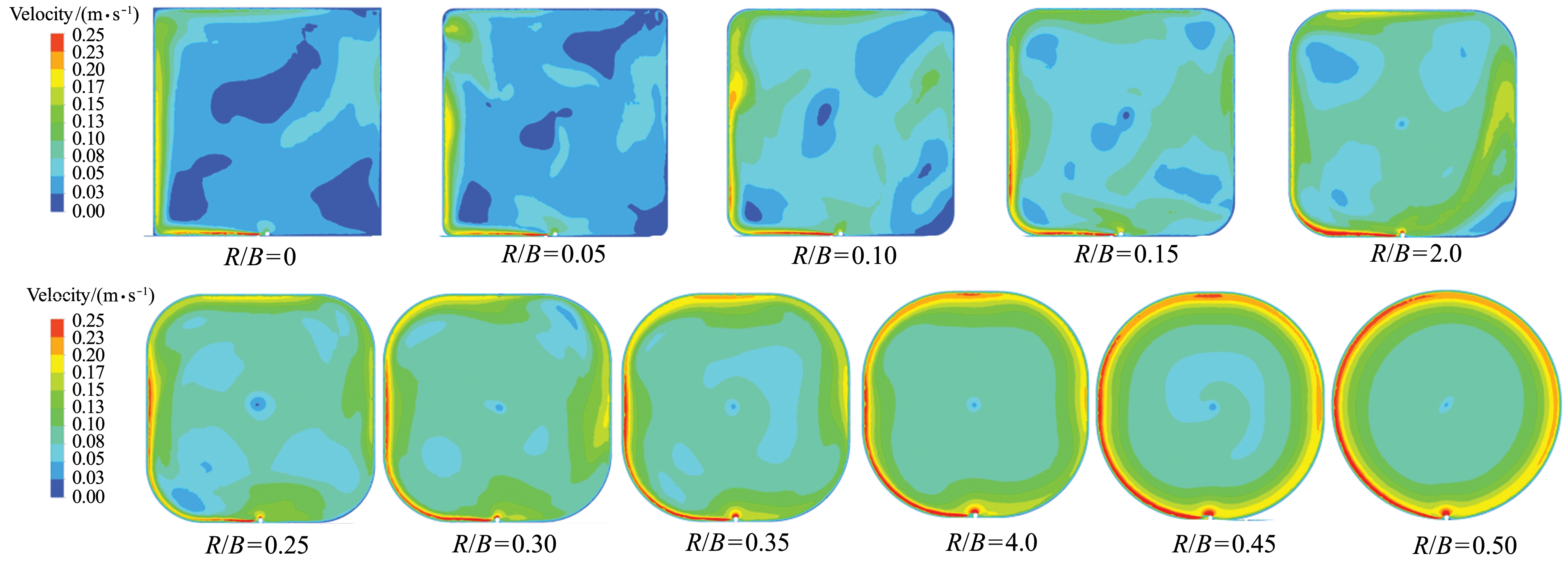
图12 不同R/B的养殖池横截面速度分布云图(Q=1174 L/h)
Fig.12 Contour maps of velocity magnitudes on the cross section in the tank with different R/B values(Q=1174 L/h)
(2)3个进水流量工况下的养殖池流场特性研究显示,养殖池内平均流速均随着R/B的增大而增大,且进水流量越大平均流速上升的趋势越明显。当0.2≤R/B<0.4时,随着R/B增大平均流速呈现平缓上升趋势;当0.0≤R/B<0.2和0.4≤R/B≤0.5时,随着R/B增大平均流速呈现较快增长趋势。随着进水流量增大养殖池流场均匀性也明显改善,养殖池系统阻力系数随R/B的变化趋势发生明显变化。
(3)由养殖池内平均流速、速度均匀系数、养殖池阻力系数和流场云图与矢量图综合分析得出,R/B=0的养殖池定义为标准方形养殖池,0<R/B<0.2的养殖池定义为近方形养殖池,0.2≤R/B<0.4的养殖池定义为方形圆弧角养殖池,0.4≤R/B<0.5的养殖池定义为近圆形养殖池,R/B=0.5的养殖池定义为标准圆形养殖池。
(4)方形圆弧角养殖池整体流速提高且流体质点运动趋于周期性震荡平衡的较规律状态,流场特征呈现一定规律性,其中R/B为0.20和0.25是兼具较好流场均匀性和高空间利用率的方形圆弧角养殖池。
[1] Ross R M,Watten B J,Krise W F,et al.Influence of tank design and hydraulic loading on the behavior,growth,and metabolism of rainbow trout(Oncorhynchus mykiss)[J].Aquacultural Engineering,1995,14(1):29-47.
[2] Timmons M B,Summerfelt S T,Vinci B J.Review of circular tank technology and management[J].Aquacultural Engineering,1998,18(1):51-69.
[3] Watten B J,Honeyfield D C,Schwartz M F.Hydraulic characteristics of a rectangular mixed-cell rearing unit[J].Aquacultural Engineering,2000,24(1):59-73.
[4] Watten B J,Beck L T.Comparative hydraulics of a rectangular cross-flow rearing unit[J].Aquacultural Engineering,1987,6(2):127-140.
[5] Behroozi L,Couturier M F.Prediction of water velocities in circular aquaculture tanks using an axisymmetric CFD model[J].Aquacultural Engineering,2019,85:114-128.
[6] 于林平,薛博茹,任效忠,等.单进水管结构对单通道矩形圆弧角养殖池水动力特性的影响研究[J].大连海洋大学学报,2020,35(1):134-140.
[7] Boersen G,Westers H.Waste solids control in hatchery raceways[J].The Progressive Fish-Culturist,1986,48(2):151-154.
[8] Wagner E J.Evaluation of a new baffle design for solid waste removal from hatchery raceways[J].The Progressive Fish-Culturist,1993,55(1):43-47.
[9] Barnes M E,Sayler W A,Cordes R J.Baffle usage in covered raceways[J].The Progressive Fish-Culturist,1996,58(4):286-288.
[10] True B,Johnson W,Chen Shulin.Reducing phosphorous discharge from flow-through aquaculture:II:hinged and moving baffles to improve waste transport[J].Aquacultural Engineering,2004,32(1):145-160.
[11] Watten B J,Johnson R P.Comparative hydraulics and rearing trial performance of a production scale cross-flow rearing unit[J].Aquacultural Engineering,1990,9(4):245-266.
[12] 张明亮.近海及河流环境水动力数值模拟方法与应用[M].北京:科学出版社,2015:3-8.
[13] Veerapen J P.Solids removal in recirculating aquaculture:the swirl separator and double-drain fish tank[D].New Brunswick:The University of New Brunswick,2003.
[14] Rasmussen M R,McLean E.Comparison of two different methods for evaluating the hydrodynamic performance of an industrial-scale fish-rearing unit[J].Aquaculture,2004,242(1-4):397-416.
[15] 刘乃硕,刘思,俞国燕.两种双通道圆形养殖池水动力特性的数值模拟与研究[J].渔业现代化,2017,44(3):1-6.
[16] Labatut R A,Ebeling J M,Bhaskaran R,et al.Exploring flow discharge strategies of a mixed-cell raceway(MCR)using 2-D computational fluid dynamics(CFD)[J].Aquacultural Engineering,2015,66:68-77.
[17] Labatut R A,Ebeling J M,Bhaskaran R,et al.Modeling hydrodynamics and path/residence time of aquaculture-like particles in a mixed-cell raceway(MCR)using 3D computational fluid dynamics(CFD)[J].Aquacultural Engineering,2015,67:39-52.
[18] Liu Yao,Liu Baoliang,Lei Jilin,et al.Numerical simulation of the hydrodynamics within octagonal tanks in recirculating aquaculture systems[J].Chinese Journal of Oceanology and Limnology,2017,35(4):912-920.
[19] 魏武.循环水圆形养殖池数值模拟及结构优化[D].湛江:广东海洋大学,2013.
[20] 俞国燕,魏武,王筱珍,等.双通道养殖池流态模拟及验证[J].渔业现代化,2012,39(6):10-14.
[21] Tvinnereim K.Design of water inlets for closed fish farms[C]//Aquaculture Engineering Technologies for the Future.The Institution of Chemical Engineers Symposium Series N°111.EFCE Publication 66,1988:241-249.
[22] Oca J,Masaló I.Design criteria for rotating flow cells in rectangular aquaculture tanks[J].Aquacultural Engineering,2006,36(1):36-44.
[23] Masaló I,Oca J.Hydrodynamics in a multivortex aquaculture tank:effect of baffles and water inlet characteristics[J].Aquacultural Engineering,2014,58:69-76.
[24] Davidson J,Summerfelt S.Solids flushing,mixing,and water velocity profiles within large(10 and 150 m3)circular ‘Cornell-type’ dual-drain tanks[J].Aquacultural Engineering,2004,32(1):245-271.
[25] Summerfelt S T,Sharrer M,Marshall C,et al.Controlling water velocity within large‘Cornell-type’ dual-drain culture tanks[C]//Proceedings of the Sixth International Conference on Recirculating Aquaculture,2006:382-393.