工厂化循环水养殖(Recirculating aquaculture system,简称RAS )是集现代化、自动化、集约化于一体的绿色健康的水产养殖模式,可做到生产过程可控,实现跨季节常年养殖,同时,该模式排放的废水废物少且方便集中处理,在稳定高产的同时对环境造成的压力较小,具有良好的社会和生态效益,已逐渐发展成为水产养殖业的主流模式之一[1-3]。然而,对于饲养密度高、饲料投喂量大的循环水养殖模式,残饵粪便等颗粒物的滞留极易在水体中产生细小颗粒物和溶解性有害物质[4]。因此,及时有效去除养殖池内的固体废弃物是RAS面临的重要问题之一。养殖池内流速的分布规律是研究池底固体废弃物运动机制的基础,养殖池内尤其是池底的流场特性直接决定了养殖池内颗粒物的运动规律及集排污性能[5]。
目前,工厂化循环水养殖中常见的养殖池池型结构主要有圆形养殖池、矩形养殖池、八角养殖池、矩形圆弧角养殖池(矩形圆切角养殖池)和跑道养殖池等。矩形圆弧角养殖池内的流场特性要明显优于矩形养殖池,且其在空间利用率、产出效率等方面要优于圆形养殖池,是循环水养殖生产中一种应用较为普遍的池形结构。由于循环水养殖池中的池形及进出水结构等涉及较多设计参数,任一参数的选择或改变都将直接影响养殖池内尤其是底部的流场特性,进而影响到养殖池系统的集排污性能。Davidson等[6]通过试验对比分析了圆形养殖池不同进水结构对水力混合性能与固体颗粒物运动规律的影响,结果表明,调整进水结构的位置和射流方向对提高养殖池内的水力混合特性产生积极的影响,适当提高池壁、池底的流速更有利于固体废弃物实现预期的去除效率。程果锋等[7]通过构建跑道式养殖池试验模型,研究了组合跑道式养殖池的工程设计参数和水力学特征,结果表明,同种射流结构条件下,增加水循环量有助于提高池水的旋转速度,增强集污效果。李琦等[8]研究了对虾高位池循环水养殖系统中不同水循环量对对虾养殖水质调控效果的影响,结果表明,提高循环水量对改善水质调控效果起到积极作用。目前,关于矩形圆弧角养殖池系统集排污的研究大多集中在对池底残饵粪便等聚集试验的图像采集和数据统计分析[9],导致养殖池池底水动力特征不明确。为此,本研究中在矩形圆弧角养殖池单进水管结构水力驱动模式下,进行了不同射流孔数(日循环次数不同)和射流管位置对养殖池系统流场特征和池底流场分布影响的数值模拟,探讨了池底水动力特性对养殖池系统集排污性能的影响,以期为工厂化循环水矩形圆弧角养殖池进水结构的参数设计和布设位置选择提供参考依据,也为探索养殖池系统的集排污性能提供理论基础。
1 数值模型
1.1 流体控制方程
水动力学的数值模拟以流体力学基本方程为基础,建立相关数学模型对养殖池系统的流体进行数值模拟分析[10]。RNG k-ε湍流模型具有广泛的适用性和合理的计算精度,且对瞬态N-S方程做时间平均处理,能更好地处理高应变率及流线弯曲程度较大的流动[11-12]。矩形圆弧角养殖池内的流动包括旋转流动和沉降[13],因而本研究中采用RNG k-ε湍流模型。本研究数值模型中假设水产养殖池系统保持恒温(不考虑温度的影响),不考虑外部环境和内部养殖对象的干扰,且流体是黏性、不可压缩的。
1.2 数值求解方法
数值模拟计算的稳定运行及其模拟结果的可信度、精度与网格质量直接相关,在兼顾高质量网格与模拟精度的同时,采用适量网格提高数值计算效率[14]。进行模拟计算前需要对网格数进行无关性验证,即随着网格数量的增加计算结果不发生显著变化[15]。本研究中,采用Fluent前处理软件Mesh进行非结构化网格划分,并对进水管、射流口、排污口等位置进行了网格加密处理。采用有限体积法求解三维N-S方程,有限差分法求解RNG k-ε湍流模型方程,求解方法采用压力隐式求解,压力速度耦合方式采用SIMPLE算法,湍流动能采用一阶迎风离散格式。
数值计算边界条件设置:入口边界为速度入口(velocity-inlet),射流速度为1 m/s,湍流强度为5.7%,水力直径为0.004 m,出口采用压力出口边界(pressure-outlet),池底边界和池壁均采用固体壁面边界,假设水面无剪切力和滑移速度,按自由界面处理,压力值为标准大气压。
1.3 水动力学特征量
流场特性对养殖系统内的生物有特定影响[16],水动力学特征量用以描述流场特性。入口冲击力(Fi)[17]、养殖池阻力系数(Ct)[18]、速度分布均匀系数(DU50)[19]和养殖池底部平均速度(v1)[20]等为常见的水动力学特征量,计算公式如下:
Fi=ρQ (vin-vavg),
(1)
(2)
DU50=v50/v1×100,
(3)
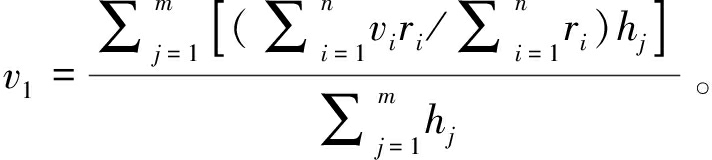
(4)
其中:ρ为水的密度(kg/m3);Q为入口流量(L/h);vin为射流入口速度(m/s);vavg为养殖池系统的平均流速(m/s);A为湿周(m2)(池底和侧壁的表面积之和);DU50接近100说明养殖池内的水流速度分布均匀且没有小涡流区域;v50为循环速度较低的50%面积的平均值(m/s);vi为所测点i的速度(m/s);ri为所测点i距离池心的水平距离(m);hj为所测点j距离水池底部的高度(m);v1为养殖池底部区域的平均速度(m/s)(设置监测点测定养殖池底部速度分布均匀性时考虑监测点相对于养殖池中心出水口的距离和距底面高度);n为同一水平面内所测点的数目(n=33);m为同一竖直面内所测点的数目(m=5)。
本研究中,对养殖池系统水体分层和流速区间做如下定义:
(1) 养殖池水深为h(m),距离池底高度为hz(m),0.00≤hz/h≤0.25为养殖池底层,0.25<hz/h<0.75为中间层,0.75≤hz/h≤1为表层。
(2) 定义0.00≤v/vavg≤0.50为低流速区间,0.50<v/vavg<1.50为中流速区间,v/vavg≥1.50为高流速区间,其中v(m/s)为所监测速度。
本研究中对v50处理时考虑了Oca等[18]提出的方程并对其略做修改,考虑到测量点所在平面相对于水池底部高度的距离,将v50值计算为每个采样点的速度加权值,其计算公式为
(5)
其中:v50j为距离池底高度为j所在截面的循环速度较低的50%面积的平均值。
2 数值模型验证
为验证数值模型建立的正确性和模拟结果的精度,将数值模型计算结果与 Oca等[21]的试验模型进行了比较。
模型参数:圆形养殖池直径为0.49 m,水深为0.06 m,底部排污口直径为0.01 m,射流口直径为0.007 m,射流速度为0.47 m/s。模型以四面体网格进行划分,对进水管、射流口、排污口等位置进行网格加密处理,网格和节点数分别为568 477和129 796,最小网格尺寸为0.000 481 m。
按照Oca等[21]方法设置一个通过圆形池中心的纵切面,在距离养殖池底面高度hz=0.03 m所在截面进行速度监测,将数值模拟结果与试验监测平均值结果进行对比(图1)。从图1可见,无论是受到出水口影响的临近养殖池中心位置、中间区域,还是接近养殖池壁的较高流速区,误差均在7%以内,且数值结果与试验结果呈现相同变化规律,二者整体吻合良好,这表明本研究中建立的数值模型合理,精度满足要求,该数值模型可以用于养殖池流场特性研究。
3 矩形圆弧角养殖池数值模型建立
本研究中数值计算选用的养殖池结构参数主要是参照现有工厂化循环水养殖池常用结构尺度,数值计算对主体结构尺度进行模型比尺缩放并对部分结构参数进行优化。
矩形圆弧角养殖池结构参数为:长L×宽B=1 m×1 m,圆弧角半径R=0.25 m,水深H=0.2 m (相对弧宽比R/B=0.25,径深比B/H=5∶1,长宽比 L/B=1∶1);进水管直径为0.02 m,进水管贴近池壁沿水深方向垂直布置,自上而下均匀设置直径为D=0.004 m的射流孔,射流孔位置与池壁间的水平距离C=0.01 m(进径比C/B=0.01),进水管的射流孔射流速度恒定为1 m/s,进水管射流孔射流方向与池壁相切(射流角度与池壁切向夹角为0°);出水口大小Dout=0.02 m,设置于池底中心位置,池底无底坡。
所建养殖池模型如图2所示(A,单根进水管布设于养殖池直壁中间位置,简称直壁单管;B,单根进水管布设于养殖池弧壁中间位置,简称弧壁单管),数值计算模型网格划分采用四面体网格,在进水管、射流口、排污口位置进行网格加密,数值计算模型网格和节点数分别为1 255 312和258 854。同时进行了网格无关性验证,与更精细的网格(网格数和节点数分别为1 502 199和317 023)进行比较,网格细化后(图3),数值计算结果无明显变化。
4 数值模拟结果与讨论
4.1 射流孔数(日循环次数)对养殖池流场特性的影响
直壁单管养殖池系统在不同射流孔数(日循环次数不同)工况下特征量统计见表1、表2,距池底高度hz=0.03、0.10、0.17 m时的速度分布云图如图4所示。调整射流孔数对养殖池内(尤其是底部)流场分布特性影响明显,随着射流孔数的增加(日循环次数增大)养殖池内平均流速明显增大(表1、图4)。射流孔数N=4的养殖池内不同水平截面水体的速度变化率为43.8%~56.3%,而日射流孔数N=21的养殖池内不同水平截面水体的速度变化率为5.1%(表2)。不同水平截面间的平均速度变化小于10%,说明养殖池系统功率损失率相对较小[22]。养殖池内的平均流速随射流孔数的增加而增大,而阻力系数Ct与池内平均速度变化呈现一定的负相关性(表1)。这是因为射流孔数增加(日循环次数增加),养殖池内水体的水力停留时间较短,单位时间输入养殖池系统的总能量增加的同时,射流水体与池壁、池底等摩擦撞击引起的能量损失消耗所占比率减小,维持水体质点间相对运动的能量消耗比率上升,进而养殖池内水体的整体流速增加,故养殖池系统的阻力系数降低。出水口处速度则随射流孔数的增多呈现增大趋势(表2),出水口处的速度增大有利于对污物的驱动进而提高集排污效率。
4.2 进水管布设位置对养殖池流场特性的影响
对矩形圆弧角养殖池中直壁单管和弧壁单管两种进水管布设位置不同的工况开展数值计算,射流方向均与养殖池侧壁相切(图2)。弧壁单管养殖池系统水动力特征量统计结果(表1)显示,当射流孔数一定时(日循环次数恒定),与直壁单管的进水结构布设位置相比,弧壁单管养殖池内平均流速较高,而养殖池系统的阻力系数Ct较低,故弧壁单管的布设有利于提高养殖池内的平均流速,同时降低养殖池系统的阻力系数Ct。
距离池底高度分别为hz=0.01、0.02、0.03、0.04、0.05 m 5个截面设置监测点(每个截面监测点取横竖和交叉4条交叉线,中心点取1个点,除中心点外每条交叉线取8个点,每个监测面共33个监测点),取5个截面监测结果的平均值计算两种进水管布设位置的养殖池底部的速度分布均匀系数DU50。
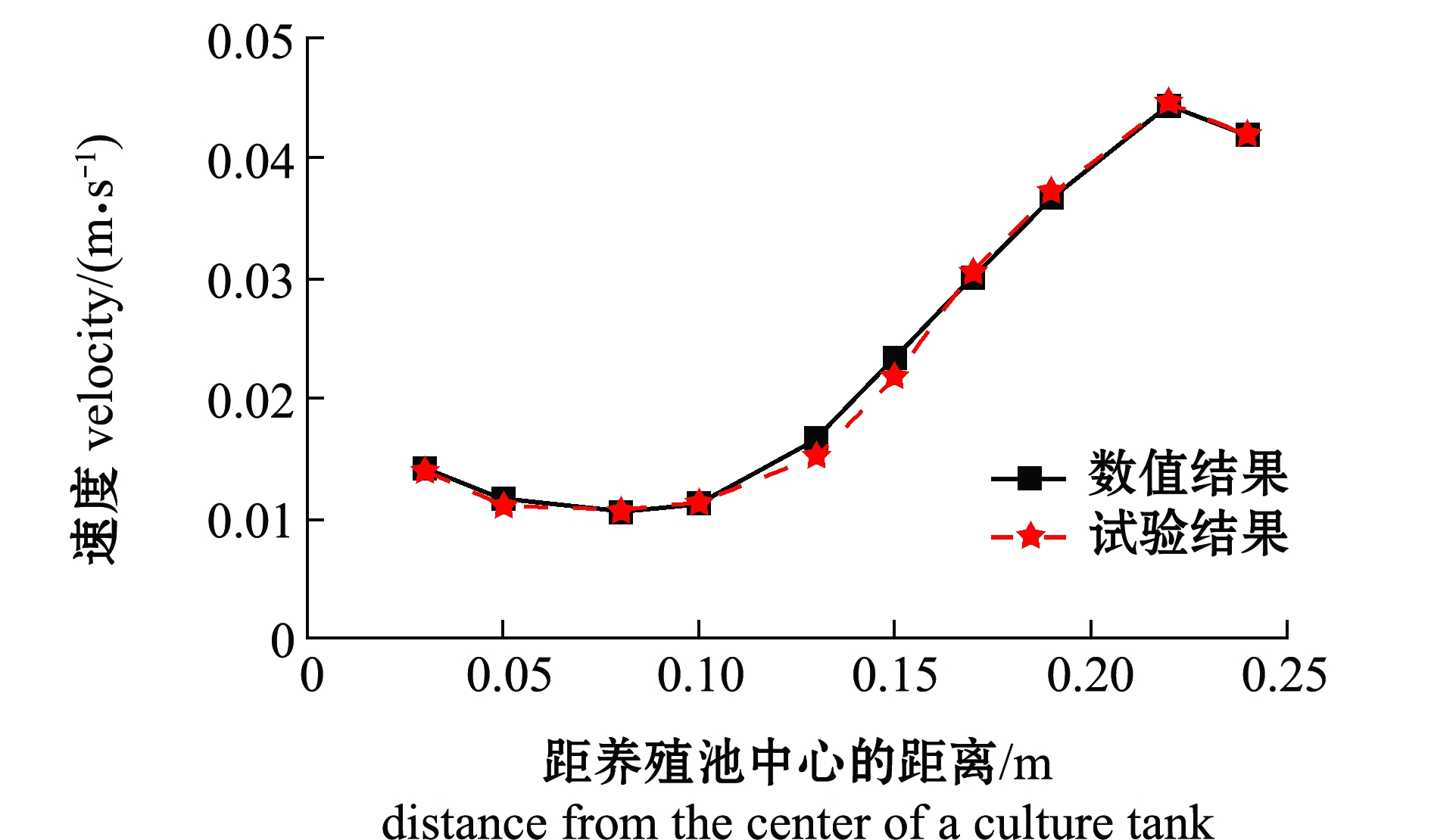
图1 圆形养殖池数值模拟结果与试验结果比较图
Fig.1 Velocity comparison of the numerical results and the experimental data in a circular tank
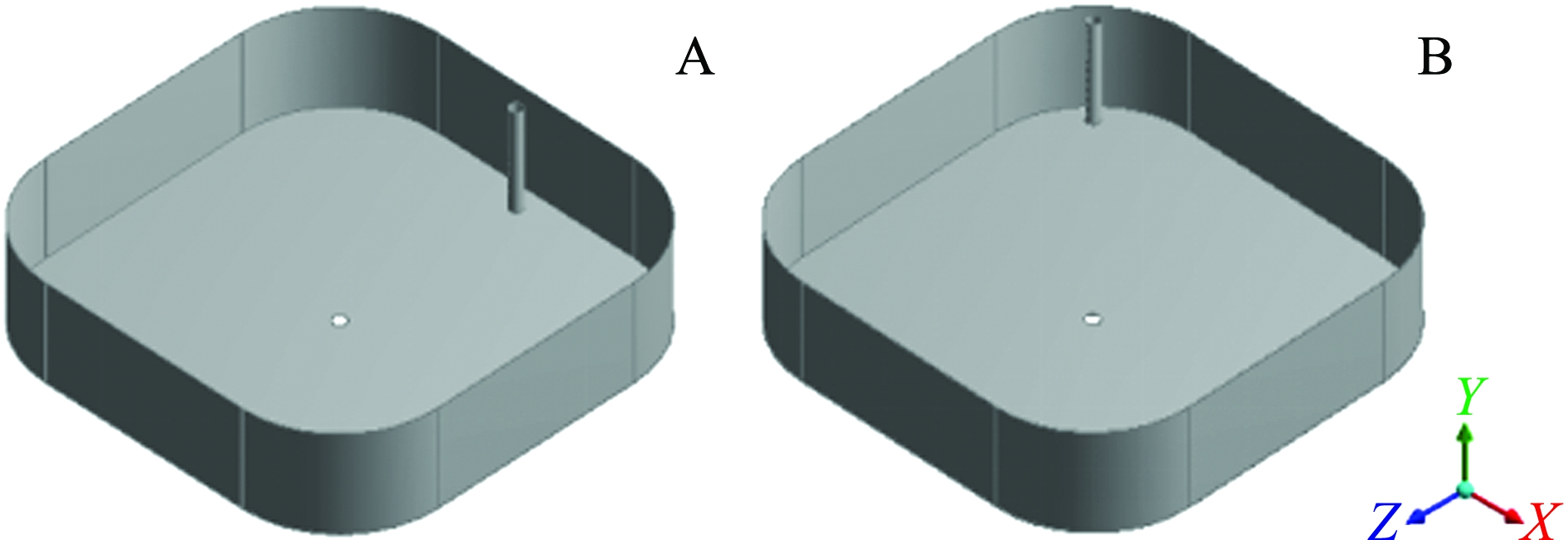
图2 直壁单管(A)和弧壁单管(B)矩形圆弧角养殖池模型图
Fig.2 Schematic diagram of a rectangular tank with arc angle model of single inlet pipe in straight edge(A) and single inlet pipe in arc edge(B)
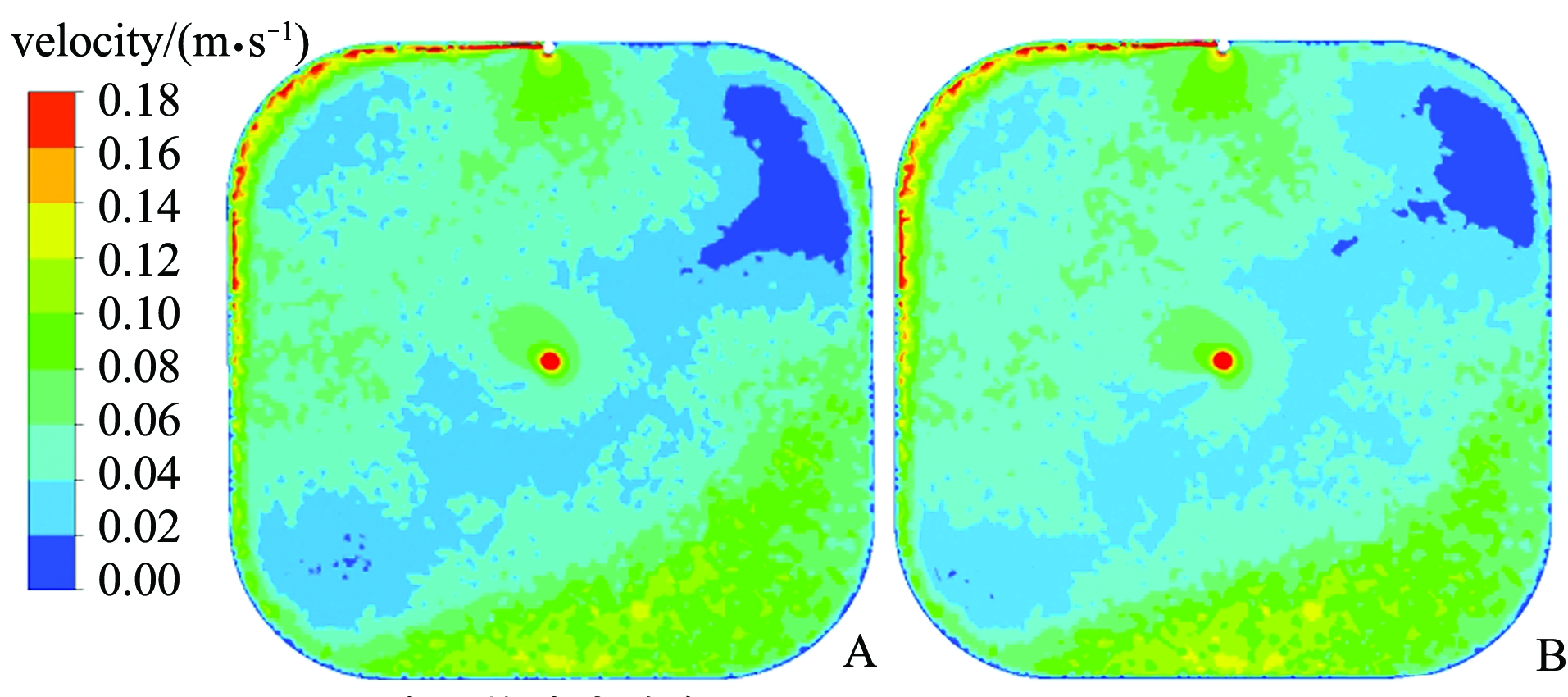
图3 网格数分别为1 255 312(A)和1 502 199(B)的速度分布云图(N=18, hz=0.10 m)
Fig.3 Contour of velocity magnitude with 1 255 312(A) and 1 502 199(B) grids(N=18, hz=0.10 m)
从表1可见,随射流孔数的增加养殖池底部速度分布均匀系数增大,而当射流孔数一定时,弧壁单管养殖池系统内平均流速、养殖池阻力系数Ct和池底速度分布均匀性均优于直壁单管养殖池系统。由于输入养殖池系统的能量主要是抵消养殖池系统阻力消耗和克服水体质点间相对运动的摩擦阻力能量损耗,从而维持养殖池系统水体运动,因此,在射流孔数较少的工况(日循环次数较低)下,抵抗养殖池系统阻力消耗占输入能量比例高,进而抵抗水体质点间相对运动的摩擦阻力能量损耗占比低,养殖池系统水体整体混合均匀性差,而在射流孔数较多(日循环次数较高)的工况下则呈现相反趋势。此外,直壁单管与弧壁单管的速度分布均匀系数差异随射流孔数的增加而减小,可见提高日循环次数(增加射流孔数)有利于提高两种进水结构布设工况的养殖池内速度分布的均匀性,此趋势也说明弧壁单管与直壁单管相比克服养殖池系统阻力消耗能量更小,进而养殖池系统水体整体呈现混合更加均匀的状态。


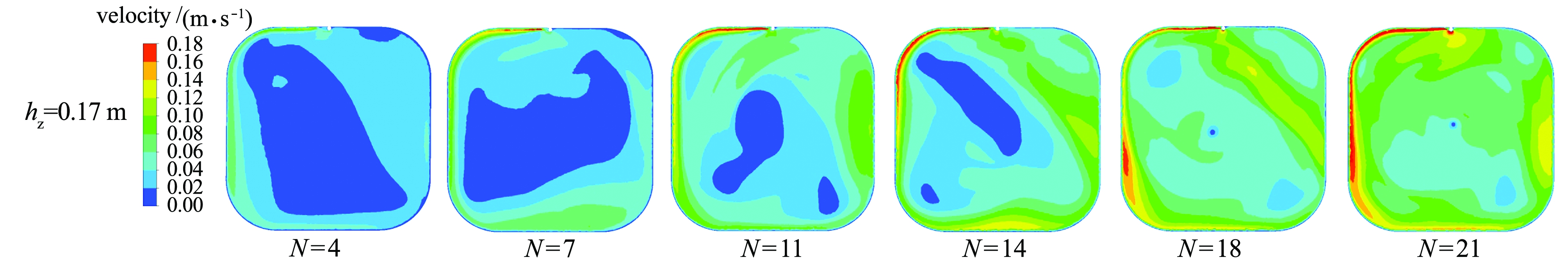
图4 直壁单管在不同射流孔数工况下3个截面的速度分布云图
Fig.4 Contour of velocity magnitudes at the 3 horizontal cross-sections in a single inlet pipe tank
表1 直壁单管和弧壁单管养殖池系统的水动力特征量统计
Tab.1 Hydrodynamic variables of single inlet pipe in straight edge and arc edg in an aquaculture tank
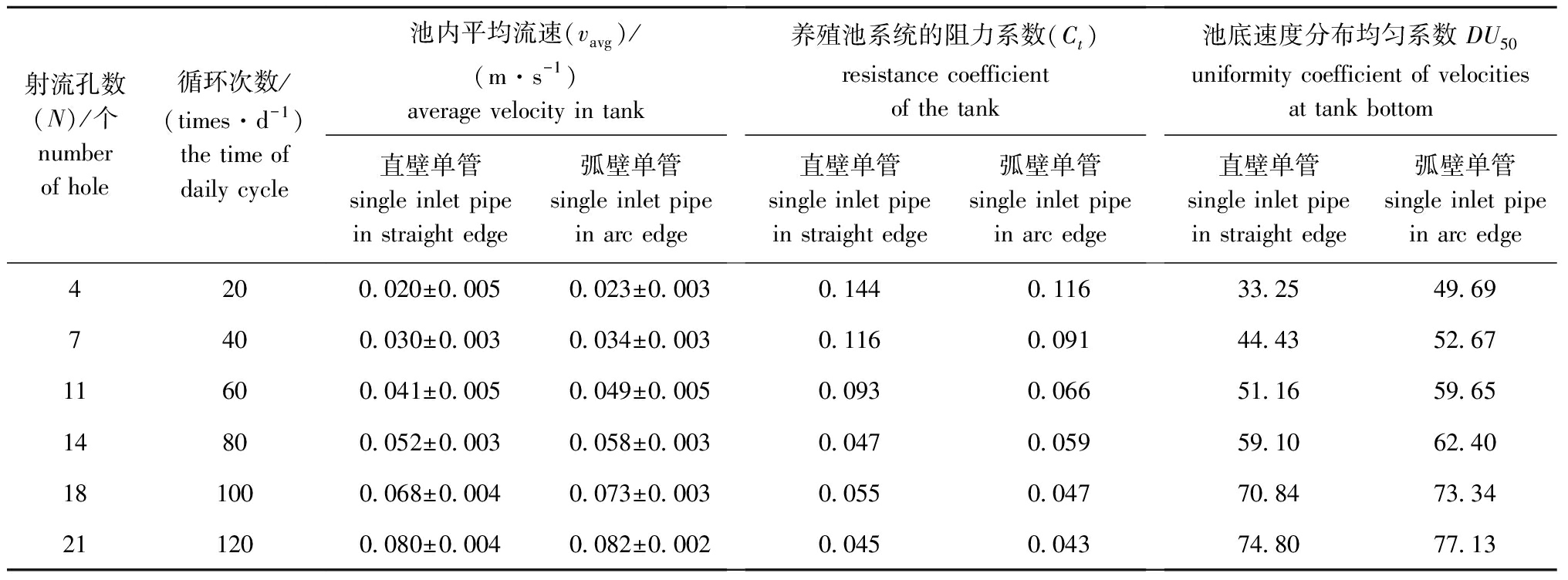
射流孔数(N)/个number of hole循环次数/(times·d-1)the time of daily cycle池内平均流速(vavg)/(m·s-1)average velocity in tank直壁单管 single inlet pipe in straight edge 弧壁单管 single inlet pipe in arc edge养殖池系统的阻力系数(Ct)resistance coefficient of the tank直壁单管 single inlet pipe in straight edge弧壁单管 single inlet pipe in arc edge池底速度分布均匀系数 DU50uniformity coefficient of velocities at tank bottom 直壁单管single inlet pipe in straight edge弧壁单管 single inlet pipe in arc edge4200.020±0.005 0.023±0.0030.1440.11633.2549.697400.030±0.0030.034±0.0030.1160.09144.4352.6711600.041±0.0050.049±0.0050.0930.06651.1659.6514800.052±0.0030.058±0.0030.0470.05959.1062.40181000.068±0.0040.073±0.0030.0550.04770.8473.34211200.080±0.0040.082±0.0020.0450.04374.8077.13
表2 直壁单管养殖池系统不同射流孔数的流速分布统计
Tab.2 Velocity distribution characteristic statistics of different jet holes in the single inlet pipe in an aquaculture tank
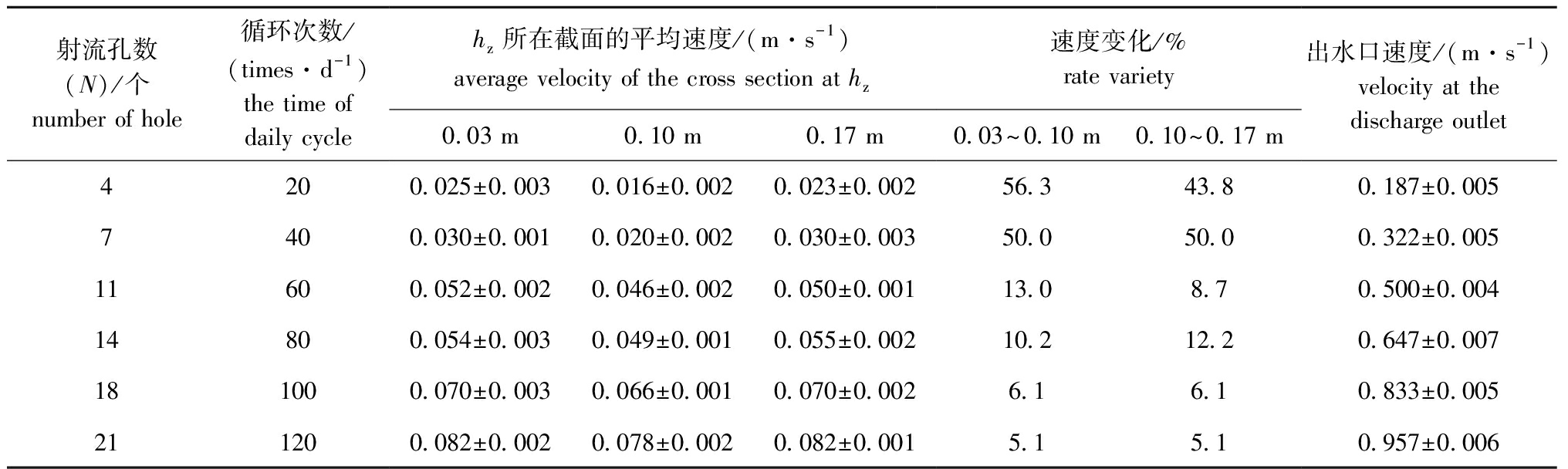
射流孔数(N)/个number of hole循环次数/(times·d-1)the time of daily cyclehz所在截面的平均速度/(m·s-1)average velocity of the cross section at hz0.03 m0.10 m0.17 m速度变化/%rate variety0.03~0.10 m0.10~0.17 m出水口速度/(m·s-1)velocity at the discharge outlet4200.025±0.0030.016±0.0020.023±0.00256.343.80.187±0.0057400.030±0.0010.020±0.0020.030±0.00350.050.00.322±0.00511600.052±0.0020.046±0.0020.050±0.00113.08.70.500±0.00414800.054±0.0030.049±0.0010.055±0.00210.212.20.647±0.007181000.070±0.0030.066±0.0010.070±0.0026.16.10.833±0.005211200.082±0.0020.078±0.0020.082±0.0015.15.10.957±0.006
图5给出了距池底高度hz=0.01、0.03、0.10 m时,直壁单管和弧壁单管两个工况的速度分布云图和速度矢量图。养殖池底部流场分布的特征将直接影响养殖池内(尤其池底)固体颗粒物如残饵粪便的分布与“迁移”。从图5可见,直壁单管在与射流方向相反的相邻圆弧角附近易出现低流速区及小漩涡区域,固体颗粒物如残饵粪便沉降后易在池底此区域沉积,对养殖池底部的残饵粪便驱动及集排污产生不利影响。与直壁单管布设位置速度矢量图相比,弧壁单管速度矢量图(图5)显示,其底部流场更加均匀,低流速区向排污中心聚集,流体质点运动轨迹更加规则,排污口附近的流动模式接近活塞流流动条件,利于固体颗粒物如残饵粪便在此处沉降,且池底四周与排污口周围形成较大的速度梯度,利于残饵粪便向排污口汇聚迁移。此外,两种进水管布设位置对养殖池底部流场分布规律的影响较明显,而对养殖池中上部空间(hz/h≥0.25)影响较小,这既有利于池底固体颗粒物如残饵粪便等向排污口汇聚迁移,又有利于养殖池上部空间溶解氧等营养物质及硝酸盐、亚硝酸盐等有害物质的均匀分布,利于养殖水体空间的功能发挥与充分利用。
湛含辉[23]在二次流现象中提出了水流推力接近理论的牛顿公式(F=ma=mRω2)。质量较小的固体颗粒物受到二次流的“搬移”作用时,由于所受离心力较小,因而与离心力方向相反的水流推力起主要作用,固体颗粒物克服了离心力的作用而汇聚到底部中心。本研究中,养殖池底部流场速度矢量图(图5)显示,弧壁单管布设工况水体在圆弧角处的运行半径总体小于直壁单管布设工况,在相同入水水流推力下,弧壁单管布设工况相比直壁单管布设工况的角速度(ω)大,因而弧壁单管布设工况二次流的现象更加明显。二次流现象存在于一切黏性流体做曲线运动过程中,并以旋转面存在于“边壁”,尤其是底部平面,因而弧壁单管布设工况在养殖池底部出现了更为明显的二次流现象,但对中上层流场的影响不大。

图5 直壁单管与弧壁单管工况下3个截面的速度矢量图与速度分布云图(N=18)
Fig.5 Vector and contour of velocity magnitudes of the 3 horizontal cross-sections at straight edge and arc edge (N=18)
5 结论
本研究中基于有限体积法和有限差分法建立三维数值计算模型,在验证的基础上对矩形圆弧角养殖池在不同日循环次数(射流孔数)、单进水管结构不同布设位置等工况下流场(尤其是池底)水动力特性进行了影响研究,得出以下结论:
(1)在计算养殖池内速度分布均匀系数DU50时考虑了其所在位置相对于养殖池底面高度,改进后的v50计算公式为
(2) 提高日循环次数(增加射流孔数)对养殖池(尤其是池底)流场特性有明显影响。随日循环次数的增加(射流孔数增加),养殖池内平均流速增加且养殖池系统的阻力系数Ct降低,其中日循环次数为100~120次/d (本研究对应射流孔数为18~21个)时,养殖池内尤其是底部能达到较优流场状态。
(3) 同一日循环次数(射流孔数恒定)工况下,弧壁单管布设位置的养殖池底部速度分布均匀性明显优于直壁单管布设位置,弧壁单管布设位置是单通道矩形圆弧角养殖池进水系统的优选布设。
[1] 唐茹霞,史策,刘鹰.循环水养殖系统管理运行存在主要问题调查分析[J].广东海洋大学学报,2018,38(1):100-106.
[2] 张振东,肖友红,范玉华,等.池塘工程化循环水养殖模式发展现状简析[J].中国水产,2019(6):34-37.
[3] 杨菁,倪琦,张宇雷,等.对虾工程化循环水养殖系统构建技术[J].农业工程学报,2010,26(8):136-140.
[4] TimmonsM B,Summerfelt S T,Vinci B J.Review of circular tank technology and management[J].Aquacultural Engineering, 1998,18(1):51-69
[5] 刘威.矩形流水对虾养殖池集污特性及对虾耐流性研究[D].舟山:浙江海洋大学,2018.
[6] Davidson J,Summerfelt S.Solids flushing, mixing, and water velocity profiles within large (10 and 150 m3) circular‘Cornell-type’dual-drain tanks[J].Aquacultural Engineering,2004,32(1):245-271.
[7] 程果锋,吴宗凡,顾兆俊,等.组合跑道式养殖池系统设计及水力学特征[J].渔业现代化,2015,42(1):6-10.
[8] 李琦,李纯厚,颉晓勇,等.对虾高位池循环水养殖系统对水质调控效果研究[J].农业环境科学学报,2011,30(12):2579-2585.
[9] 赵乐,张清靖,李宏伟,等.循环水养殖系统管式射流集排污特性试验研究[J].渔业现代化, 2016,43(4):16-21.
[10] 张明亮.近海及河流环境水动力数值模拟方法与应用[M].北京:科学出版社,2015:3-8.
[11] 王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004:121-125.
[12] 丁欣硕,刘斌.Fluent17.0流体仿真从入门到精通[M].北京:清华大学出版社,2018:14-16.
[13] Liu Yao,Liu Baoling,Lei Jilin,et al.Numerical simulation of the hydrodynamics within octagonal tanks in recirculating aquaculture systems[J].Chinese Journal of Oceanology and Limnology,2017,35(4):912-920.
[14] 孙赟,林亚玲,刘兴静,等.涡轮反应器气固两相流动反应CFD模型数值模拟[J].农业机械学报,2013,44(8):195-201,212.
[15] 喻黎明,徐洲,杨具瑞,等.基于CFD-DEM耦合的网式过滤器水沙运动数值模拟[J].农业机械学报,2018,49(3):303-308.
[16] 杨宇,严忠民,乔晔.河流鱼类栖息地水力学条件表征与评述[J].河海大学学报:自然科学版,2007,35(2):125-130.
[17] Benoit D.Hydrodynamic characteristics of muti-drain circular tanks[D].Fredericton: The University of New Brunswick,2007.
[18] Oca J,Masaló I.Flow pattern in aquaculture circular tanks:influence of flow rate, water depth, and water inlet & outlet features[J].Aquacultural Engineering,2013,52:65-72.
[19] Masaló I,Oca J.Influence of fish swimming on the flow pattern of circular tanks[J].Aquacultural Engineering,2016,74:84-95.
[20] Venegas P A,Narv es A L,Arriagada A E, et al.Hydro-dynamic effects of use of eductors (jet-mixing eductor) for water inlet on circular tank fish culture[J].Aquacultural Engineering,2014,59:13-22.
es A L,Arriagada A E, et al.Hydro-dynamic effects of use of eductors (jet-mixing eductor) for water inlet on circular tank fish culture[J].Aquacultural Engineering,2014,59:13-22.
[21] Oca J,Masaló I,Reig L.Comparative analysis of flow patterns in aquaculture rectangular tanks with different water inlet characteristics[J].Aquacultural Engineering,2004,31(3-4):221-236.
[22] Burley R,Klapsis A.Flow distribution studies in fish rearing tanks. Part 2-Analysis of hydraulic performance of 1m square tanks[J].Aquacultural Engineering,1985(2):113-134.
[23] 湛含辉.二次流现象及其初步研究[J].株洲工学院学报,2001,15(3):27-29.