港口货物吞吐量变动受世界贸易波动、短期区域经济发展状况、海运市场运力供需平衡和自然环境等多重因素共同影响。实现精准预测对于港口的正常运营、规划建设和发展期望,具有重大现实意义。目前,用于预测研究的方法较多[1],其中,人工神经网络法[2-3]优势为特有的非线性适应性信息处理能力,但存在陷于局部最优等问题。时间序列模型法[4]优点是可对已有的历史数据进行较好预测,不足之处在于对信息波动反馈的滞后性。支持向量机(SVM)法[5-13]在非线性小样本预测领域具有先进性,但在港口多品种货物吞吐量预测尚未见报道。
目前对于货物吞吐量的研究方法主要有移动平均法、人工神经网络方法等,大多基于以年为单位的数值预测[14-15],而应用支持向量机模型对数据预测以月为单位的研究更为微观,精度更好。本研究中,以大连港典型货种煤炭、油品、集装箱作为研究对象,结合直接和迭代预测模型的优点,构建了基于支持向量机的多步混合预测模型,根据以往单步预测和迭代预测的优势,结合支持向量机这一机器学习模型在预测领域的最新应用,通过对大连港2012年1月—2017年6月共66个月吞吐量样本数据进行实证分析,确定其预测准确性,旨在为港口多货种吞吐量预测提供技术支持。
1 支持向量机模型预测原理
支持向量机(Support vector machine,SVM)模型的基本预测原理是将已知样本数据映射到高维特征空间,将原问题转化为最优回归超平面的二次规划的求解问题,实现在特征空间中利用简单的线性回归方法求解复杂的非线性问题的目的。适合于小样本情况下的预测分析。
给定一组关系未知的样本(x1,y1),(x2,y2),…,(xi,yi)(xi∈X⊆Rn,yi∈Y⊆Rn),SVM可以利用非线性映射φ将xi映射到高维特征空间H,并在这个空间进行线性逼近,用公式描述为
f(x)=ω·φ(x)+b。
(1)
其中:ω是超平面的权值向量;b为偏置项。
求解回归系数ω和b,利用统计学习理论,可以将问题转化为求解一定约束条件下的最小化规则化风险泛函:
(2)
s.t.:yi-ω·φ(xi)-b≤ε+ξi,
(3)
(4)
其中,约束条件C>0调节超出误差ε的惩罚水平,其表达的含义如图1所示。
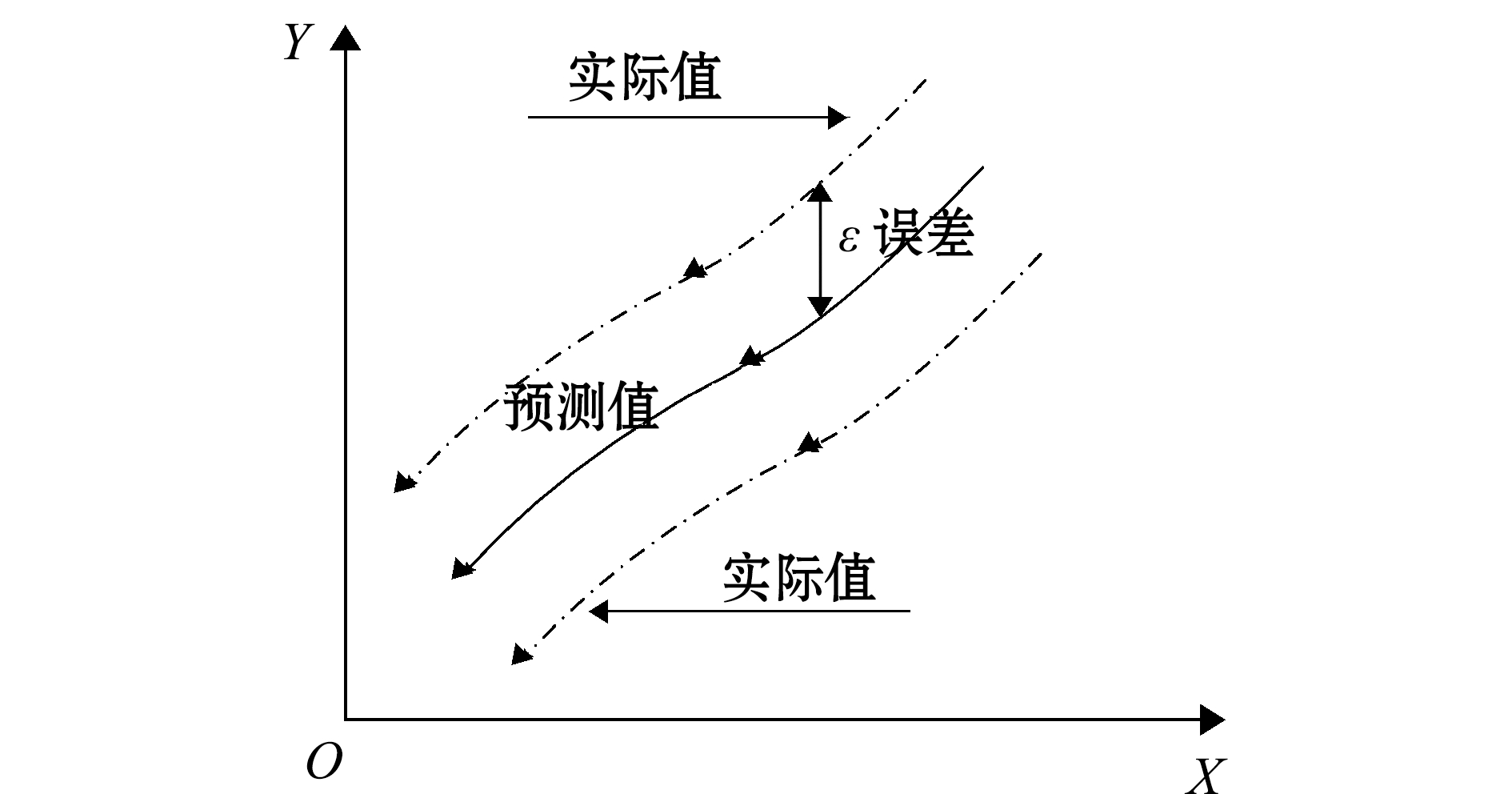
图1 SVM回归分析参数
Fig.1 Parameters for the support vector machine regression
式(2)是凸二次优化问题,通常需转化为对偶问题进行求解:
(5)
其中:L为拉格朗日算符;![]() 为拉格朗日乘子;
为拉格朗日乘子;![]()
对初始变量分别求偏导:
(6)
(7)
∂ξiL=C-ai-η=0,
(8)
(9)
求解后可以得到:
(10)
这样有
(11)
定义K(xi,xj)=φ(xi)·φ(xj),则得到:
(12)
其中,K(xi,xj)为向量xi和xj在特征空间φ(xi)和φ(xj)上的内积,称为核函数。核函数具有直接在输入空间上计算的特点,不必映射到高维空间。
2 多步混合预测模型的构建
对于港口吞吐量进行预测,常规的直接预测方法和以每个目标期依次进行的迭代预测方法各有其自身的优势。直接预测是对指定时间的吞吐量进行单步预测,无迭代预测过程,因此,性能更准确,误差更小。
直接预测的方法如表达式(1)~(3),每一步预测均需训练不同的SVM模型,即
SVM(1):Indexk+1=f(Indexk,Indexk-1,...,
Indexk-n+1),
(13)
SVM(2):Indexk+2=g(Indexk,Indexk-1,...,
Indexk-n+1),
(14)
⋮
SVM(γ):Indexk+γ=h(Indexk,Indexk-1,...,
Indexk-n+1)。
(15)
而迭代预测的方法如表达式(4)、(5),可通过一次训练的SVM模型循环使用,依次预测出各目标期的数据,即
Indexk+1=f(Indexk,Indexk-1,...,
Indexk-n+1),
(16)
Indexk+2=f(Indexk+1,Indexk,...,
Indexk-n+2),
(17)
⋮
Indexk+γ=f(Indexk+γ-1,Indexk+γ-2,...,
Indexk+γ-n)。
(18)
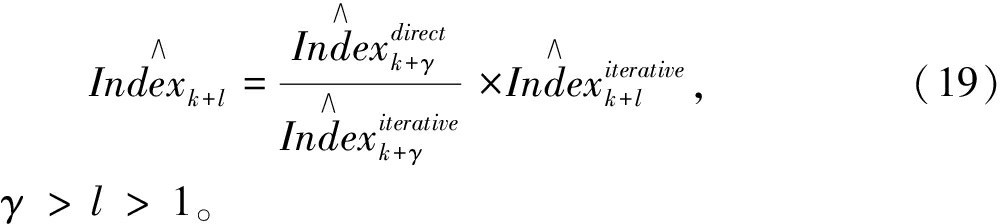
本研究中将直接预测与迭代预测相结合,提出了一种吞吐量多步混合预测模型。假设第一个控制点是第k个月,第二个控制点是第k +γ个月,仅使用一步步长的直接预测来预测指标被认为是准确的。因此,首先认为下个月k+1和下一个控制点(即第k+γ个月)的预测是准确的。因此,调整操作用于在第k+1个月之后改善预测值。具体流程如图2所示。
迭代预测模型重复使用单步预测模型直接预测下月的吞吐量指标,不需要开发多个SVM预测模型,但预测误差会在重复预测过程中累积。本研究中将直接预测与迭代预测相结合,提出了一种港口吞吐量多步混合预测模型。通过组合直接预测模型和迭代预测模型,直接预测模型中控制点的预测值可用于多步预测模型中调整两个控制点之间的预测值。迭代预测可以分解为一些子预测,在每个子预测中使用基本预测,并且将参数设置为1。
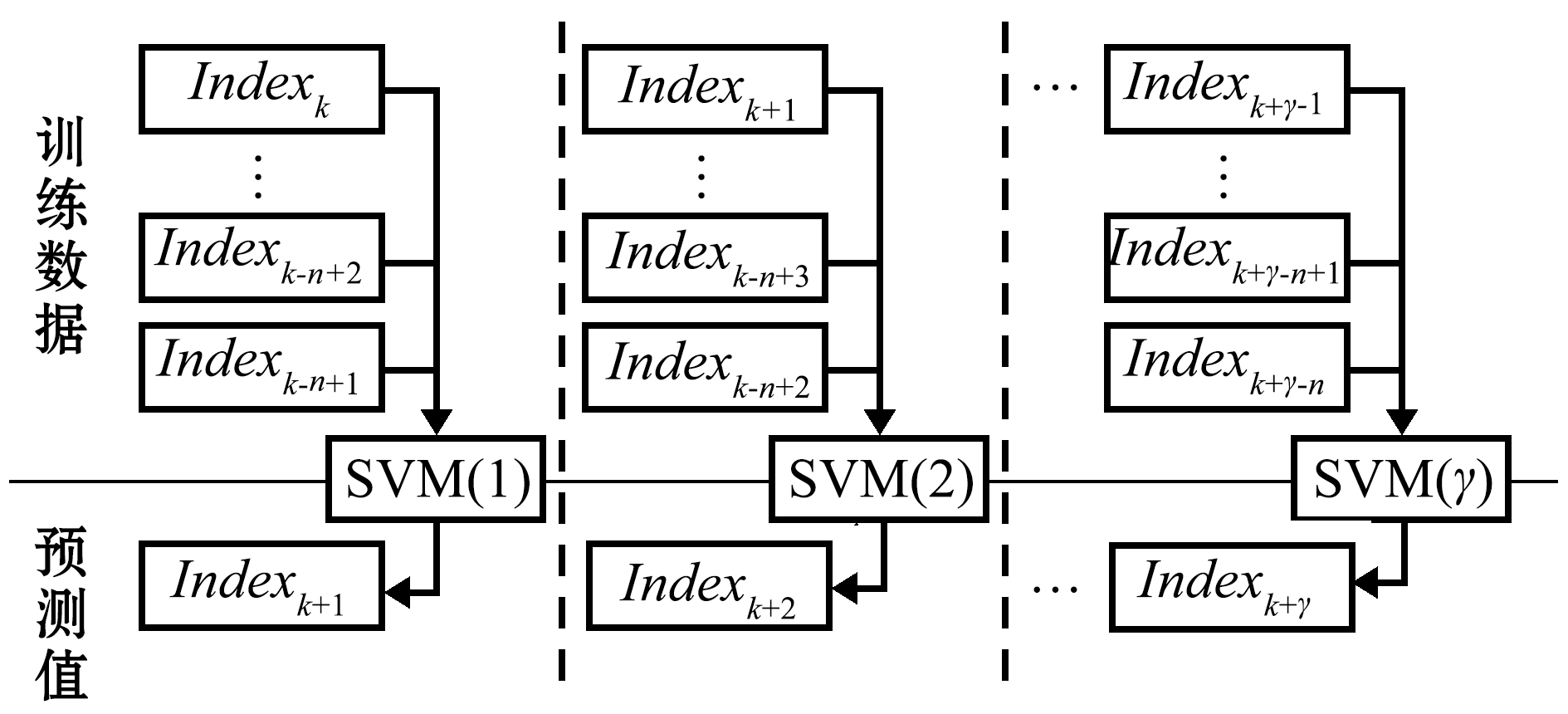
图2 迭代预测流程
Fig.2 Structure of iterative prediction model
在迭代预测模型中,首先将前n个月的指标即Indexk、Indexk-1、…、Indexk-n+1作为输入向量以通过SVM(1)进行单步直接预测Indexk+1,第二步是使用SVM(2)预测Indexk+2。在此之前,应该更新输入向量,即通过加入最新预测值Indexk+1和消除对预测目标期影响最小的状态向量Indexk-n+1,这样既保持状态向量总数不变,保证了状态向量的最佳选取精度。最后,通过上述迭代,可以预测目标的指标。在迭代预测过程中,SVM模型是唯一的,输入向量是变化的。迭代预测的具体步骤如图3所示。
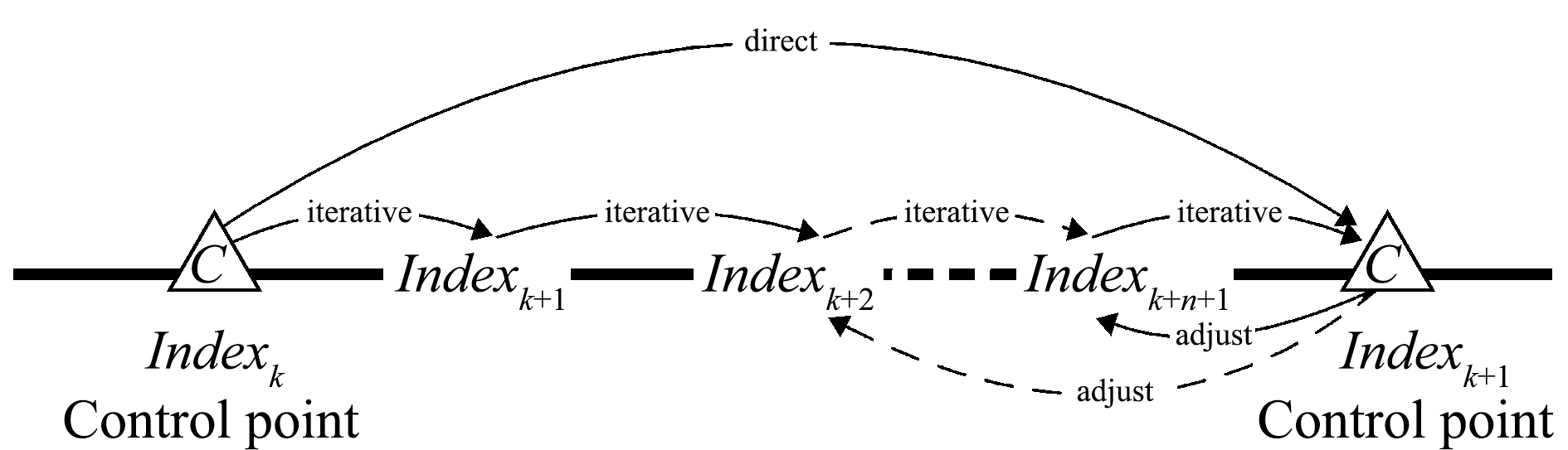
图3 多步混合预测流程
Fig.3 Process of iterative a multi-step hybrid prediction model
3 实证分析
3.1 数据选取
本研究中选取大连港口流通货物中的典型货种煤炭、油品和集装箱作为研究对象,以2012年1月—2017年6月共计66个月的月度吞吐量为样本数据。每种货物的月度吞吐量数据如图4所示,其中,煤炭月度吞吐量最高为178万t,最低为78万t;油品月度吞吐量最高为820万t,最低为357万t;集装箱月度吞吐量最高为1265万t,最低为583万t。
从吞吐量变化幅度来看,煤炭的数据波动相对较小,油品和集装箱波动的幅度较大。总体来说,货物吞吐量的波动主要是由世界经济大环境下运力供需的变化及一年中货物周期波动所引起的。对于集装箱货物,其涉及的种类和数量繁多复杂,由于生产特性或原材料的自然生长周期特点,很多商品具有明显的季节性与周期性波动,因此,从图4可以看出,集装箱吞吐量具有较为明显的周期性波动变化规律。对于油品类货物,其吞吐量除受季节性供需波动影响,国际经济政治方面的影响也较明显,尤其受中东地区战争及国际社会对伊朗、俄罗斯的制裁冲击较为明显,当国际社会对伊朗、俄罗斯原油出口限制放宽时,中国沿海各港口的原油类产品进口均有明显提升。对于煤炭种类货物,大连港流通的主要构成为内蒙古等地运输至南方沿海各港口的煤炭,受外贸影响较小,一般波动主要为季节性因素造成,相对于集装箱和油品类货物,其吞吐量相对比较稳定。
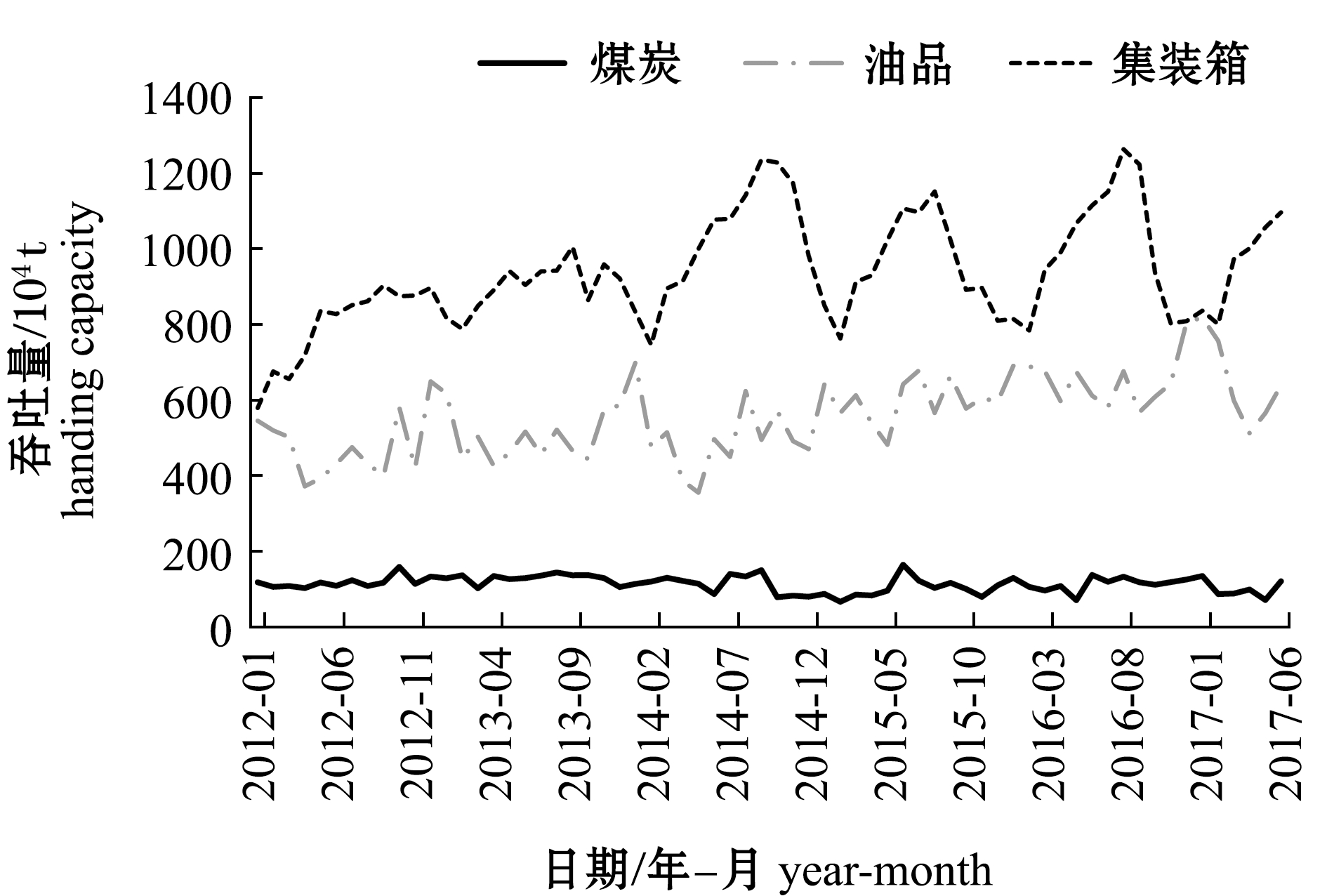
图4 主要货种吞吐量月度走势
Fig.4 Historical data of monthly average throughput of main cargos
3.2 SVM训练
利用SVM机器学习方法进行预测的主要步骤,首先是对现有数据进行量纲归一化处理,然后对模型依据处理后的数据进行训练。归一化转换方式为
(20)
其中:Smax为样本序列中的最大值;Smin为样本序列中的最小值;![]() 为归一化后的值;Si为原始数值。
为归一化后的值;Si为原始数值。
通过训练比较,得到利用预测目标月份前连续52个月度(2013年3月至2017年6月)吞吐量数据作为输入,后续6个月的数据作为输出的训练方式获得的SVM,对吞吐量原始序列具有最好的拟合效果。具体实施过程:将58组吞吐量样本数据进行归一化处理,得到一个3×58的矢量矩阵,并将相对应的后续6个月的吞吐量处理成一个3×6的矢量,作为输出数据;把样本数据输入SVM进行预测时,将数据分为训练组、检测组和验证组3组,3组数据占全部样本数据的比例分别为80%、10%和10%,按此比例,在58组数据中抽取6组数据作为检测数据,另外抽取6组数据进行验证,剩余46组数据作为SVM的训练数据。
首先,通过对训练组数据的SVM训练,得到具有不同核函数及参数配置的SVM模型。然后将后续6个月的吞吐量数据输入到当前的SVM中进行拟合检验,计算拟合值与实际数据间的偏差。其中,偏差最小时的核函数和参数值为本研究的最优SVM模型。
4 预测结果
以预测结果与实际值比较的平均相对误差(MAPE)和相关系数(βxy)来评判模型的有效性。
MAPE=![]()
100%。
(21)
其中:Sm(t+1)为m品类货物第t+1个月对应的实际吞吐数量;Sm,k(t+1)为m品类货物第t+1个月对应的预测吞吐量。
预测值和实际值的相关系数βxy计算公式为
(22)
其中:Cov(x,y)为x、y的协方差;D(x)、D(y)为x、y的方差。
应用网格搜索的方式确定参数C和ε的最优值为0.308、0.003。笔者取2017年7—12月为预测目标月份,经过数据试算,表达式(19)中取γ=9时,预测精度最高。利用2013年3月至2017年6月共计52个月大连港的油品、集装箱、煤炭吞吐量作为数据库进行训练,将所得的2017年7月至2017年12月共计6个月的预测数据与实际吞吐量及传统预测方法对比,结果如图5~图7所示,可以看出,本模型预测性能优于传统预测方法。
为检验模型的实际预测性能,本研究中将预测结果与10%验证组数据对比,并计算预测数据与实际数据的相关系数。综合比较结果如表1所示,其中,3个货种的预测港口吞吐量走势与实际情况基本一致,除去个别月份,本研究中所提出的模型基本可以预测未来短期内港口各主要货种的吞吐量变化趋势。3种主要货种相比较,集装箱的吞吐量预测精度最高,证明了模型在预测集装箱吞吐量方面性能更佳。其主要原因在于集装箱的吞吐量可更多反映外贸运行情况,综合各年月份,其吞吐量波动更容易把握。相比较而言,油品和煤炭的预测精度稍差,主要原因在于2017年国际能源走势变化较大,尤其是石油价格受政治、战争等因素影响较多,更不易把握未来走势,因此,在港口吞吐量上更易显出其不确定性。
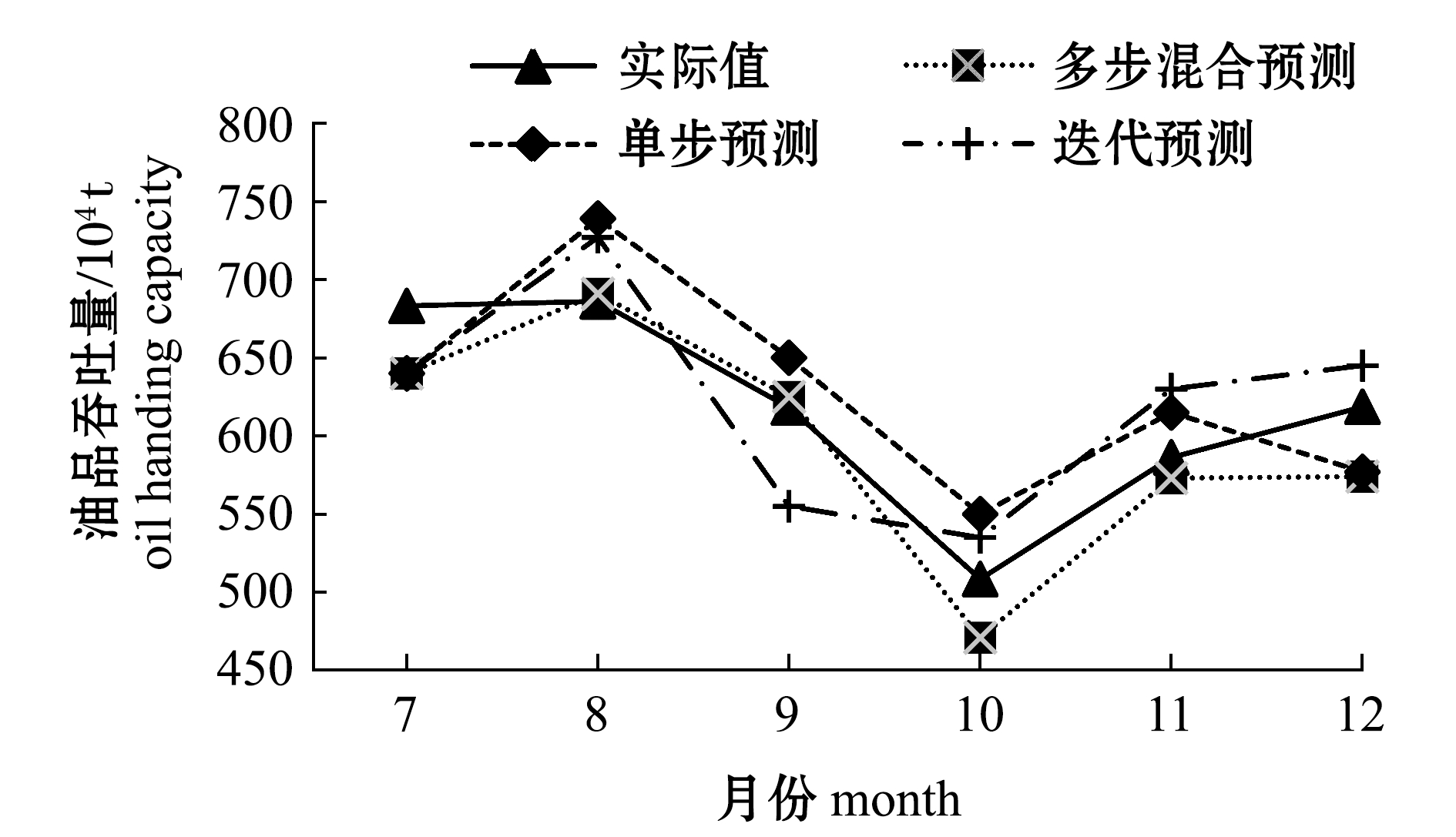
图5 2017年油品吞吐量预测数据与实际值对比图
Fig.5 Comparison of oil throughput predicted data with actual values in 2017
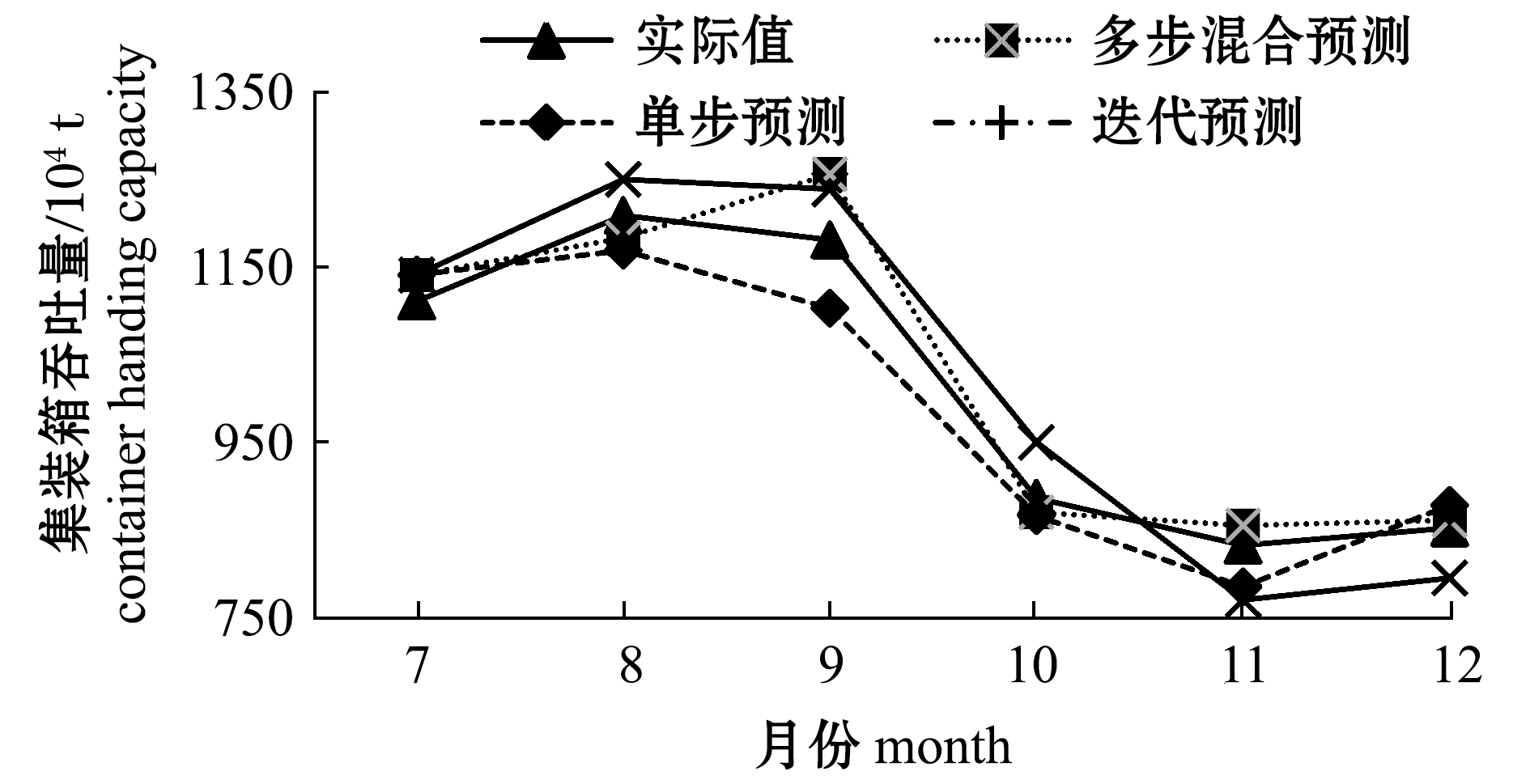
图6 2017年集装箱吞吐量预测数据与实际值对比图
Fig.6 Comparison of container throughput predicted data with actual values in 2017
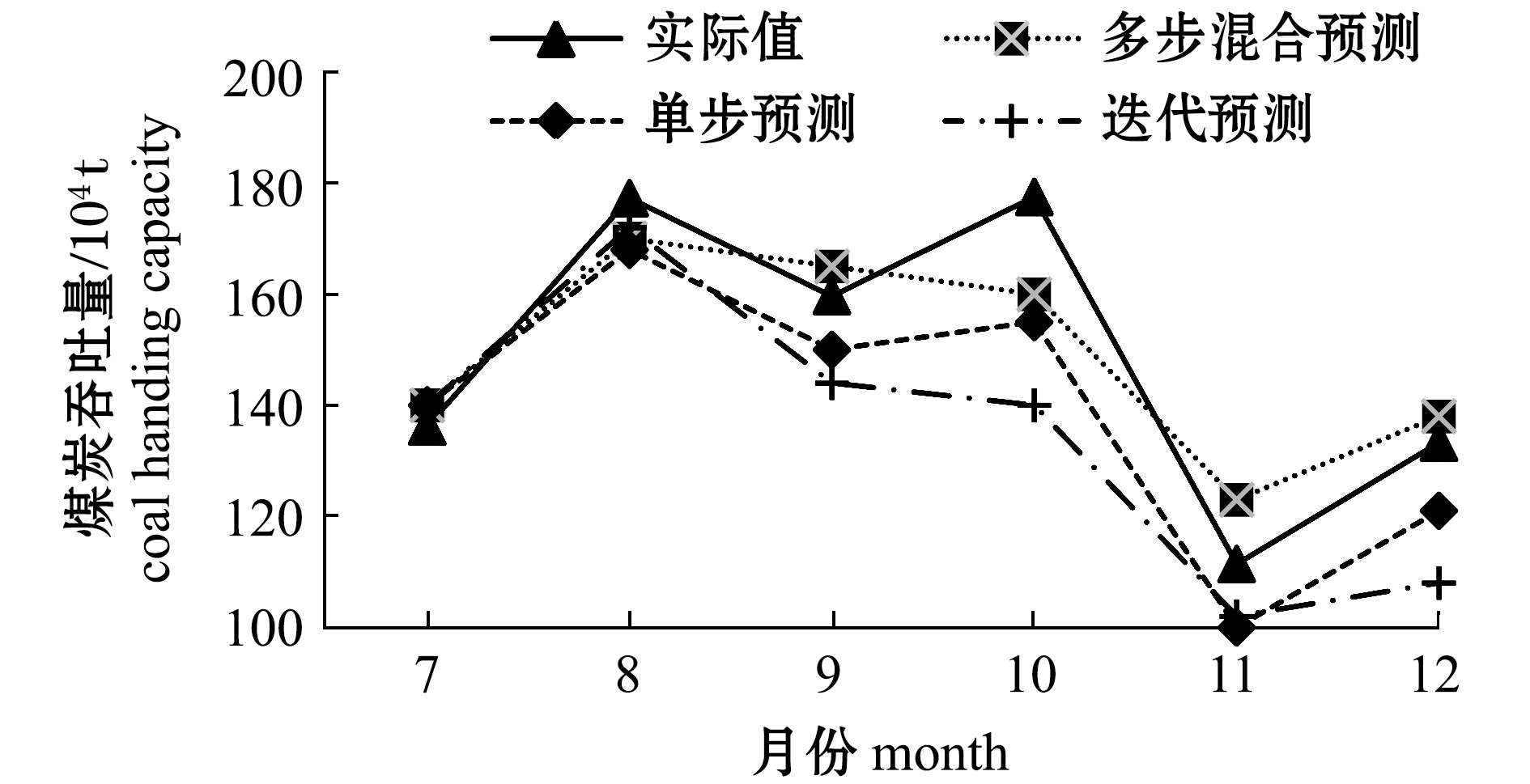
图7 2017年煤炭吞吐量预测数据与实际值对比图
Fig.7 Comparison of coal throughput predicted data with actual values in 2017
表1 3种主要货物预测值与实际值的平均相对误差和相关系数
Tab.1 Average relative error and correlation coefficient between predicted and actual values of the three main cargos %
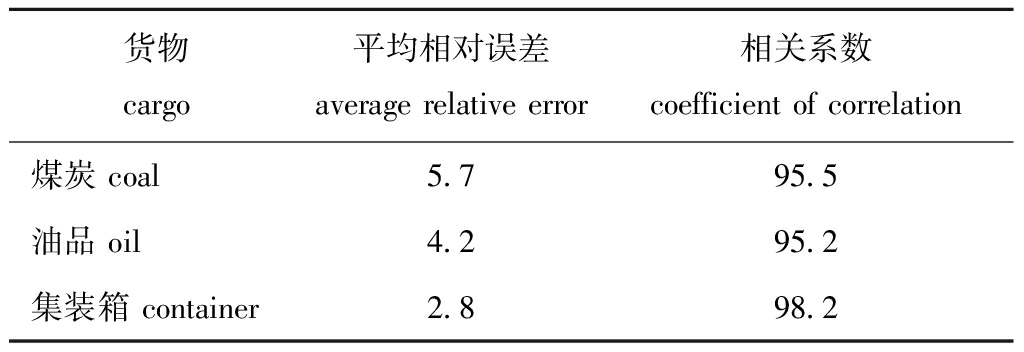
货物cargo平均相对误差average relative error相关系数coefficient of correlation煤炭 coal5.795.5油品 oil4.295.2集装箱 container2.898.2
5 结论
(1)本研究中以基于支持向量机的方法构建了多步混合预测模型,实证分析结果表明,该模型设计合理,参数标定准确,预测精度较高。
(2)本研究中结合直接和迭代预测模型的优点构建多步混合预测模型,在同类研究中具有先进性。
(3)本研究中构建的多步混合预测模型,可为港口经营者掌握港口运转状态及未来一段时间内经营决策提供参考,在港口多货种吞吐量指标预测中具有可行性。
[1] DeLurgio S A.Forecasting Principles and Applications[M]. Boston,MA:Irwin/McGraw-Hill,1998.
[2] 占祖桂.基于BP神经网络的香港离岸人民币汇率预测[J].吉林金融研究,2018(8):44-46.
[3] 马广慧,马豆豆,邵秀丽.基于遗传BP神经网络的三七价格预测[J].天津师范大学学报:自然科学版,2017,37(6):76-80.
[4] 王力,张超.机场能耗的时间序列混合预测方法[J].中国民航大学学报,2017,35(6):31-35.
[5] Dong Bing,Cao Cheng,Lee S E.Applying support vector machines to predict building energy consumption in tropical region[J].Energy and Buildings,2005,37:545-553.
[6] Guo Xuesong,Sun Linyan,Li Gang,et al.A hybrid wavelet analysis and support vector machines in forecasting development of manufacturing[J].Expert Systems with Applications,2008,35(1-2):415-422.
[7] 居锦武.基于LS-SVM的养殖水体氨氮含量分析模型的优化[J].大连海洋大学学报,2016,31(4):444-448.
[8] 吴建新.基于ALI模型的沿海港口集装箱吞吐量短期预测分析[J].港口经济,2016(9):26-28.
[9] 徐峰,范春菊,徐勋建,等.基于变分模态分解和AMPSO-SVM耦合模型的滑坡位移预测[J].上海交通大学学报,2018,52(10):1388-1395,1416.
[10] 叶子奇,蒋惠园,冯琪,等.基于GA-SVM模型的长江干线港口集装箱需求量预测[J].水运管理,2018,40(4):18-22.
[11] 赵合胜.基于灰色预测和SVM的茶叶烘焙温湿度预测[J].西安文理学院学报:自然科学版,2018,21(5):64-67.
[12] 王定成,方廷健,高理富,等.支持向量机回归在线建模及应用[J].控制与决策,2003,18(1):89-91,95.
[13] 关峰.基于运营环境不确定性的不定期船调度研究[D].大连:大连海事大学,2018.
[14] 吴琛.基于时间序列模型的港口集装箱吞吐量预测[J].珠江水运,2019(5):73-74.
[15] 张树奎,鲁子爱.港口集装箱吞吐量的灰色神经网络预测模型研究[J].江苏科技大学学报:自然科学版,2014,28(3):216-219.