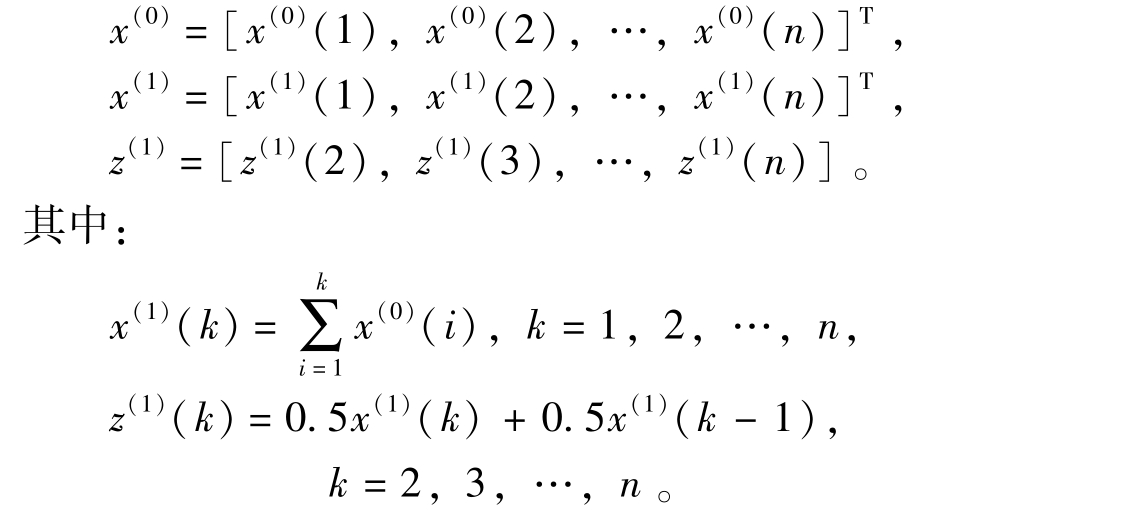
摘要:为研发溢油污染事故后续修复和渔业生产恢复辅助决策系统,采用灰色预测模型与线性内插法相结合的数学方法,构建溢油灾后生物修复降解率辅助决策模型并进行实证研究。结果表明:构建的模型预测精度为93.65%~97.53%,预测模型是可行的。研究表明,基于灰色预测模型与线性内插法相结合的建模方法有效地解决了溢油灾后生物修复模拟试验中局部数据序列非等时距的建模问题,能够满足建立生物修复降解率辅助决策模型的需要,能够对溢油灾后修复与渔业生产恢复进行中长期决策提供辅助支持。
关键词:灰色预测模型;线性内插法;生物修复;降解率;辅助决策模型
近年来,国内关于生物修复方面的研究在文献计量结果上呈现持续上升的趋势。如沈伟航等[1]研究了石油污染土壤生物修复过程中毒性的植物指示;朱文英等[2]研究了小麦秸秆生物炭对石油烃污染土壤的修复作用;何洁等[3]研究了翅碱蓬栽培对原油污染土壤理化性质的影响;樊鑫[4]研究了在实验室条件下模拟盐沼湿地生态系统,应用湿地微宇宙和慢性毒性试验方法,以沙蚕、翅碱蓬和降油细菌功能群为生物修复主体,进行不同石油污染浓度底质的修复试验。同时,生物修复已在石油污染修复方面得到了实际应用。2010年7月16日,大连湾输油管道爆炸事故清理初期,投施了23 t修复微生物,用于清理港口海域183 km2的浮油,这是人类首次大规模应用生物修复技术治理海上溢油污染并取得了良好效果[5]。
在溢油污染事故后续修复和渔业生产恢复辅助决策系统研发中,辅助决策模型的构建是研究核心,关系到辅助决策的科学性和准确性。因此,开展溢油灾后生物修复辅助决策模型的研究具有重要意义。但有关生物修复中长期决策数学模型的研究尚未见报道。鉴于实验室生物修复模拟试验数据呈现“小样本、贫信息”及观测时间存在局部非等时距的特点,本研究中通过灰色预测模型和线性内插法相结合,建立生物修复降解率预测模型,以期为溢油灾后修复进行中长期决策提供辅助支持。
灰色系统理论是1982年由中国著名学者邓聚龙教授创立,是“以部分信息已知,部分信息未知的小样本、贫信息”不确定性系统为研究对象的一门系统科学新学科[6]。其应用领域已十分广泛,涉及系统分析、工业控制、经济预测和管理决策等众多领域[7]。
设x(0)为非负的原始数据序列,x(1)为x(0)的1次累加生成数据序列,z(1)为数据序列x(1)的邻均值等权生成序列,即:
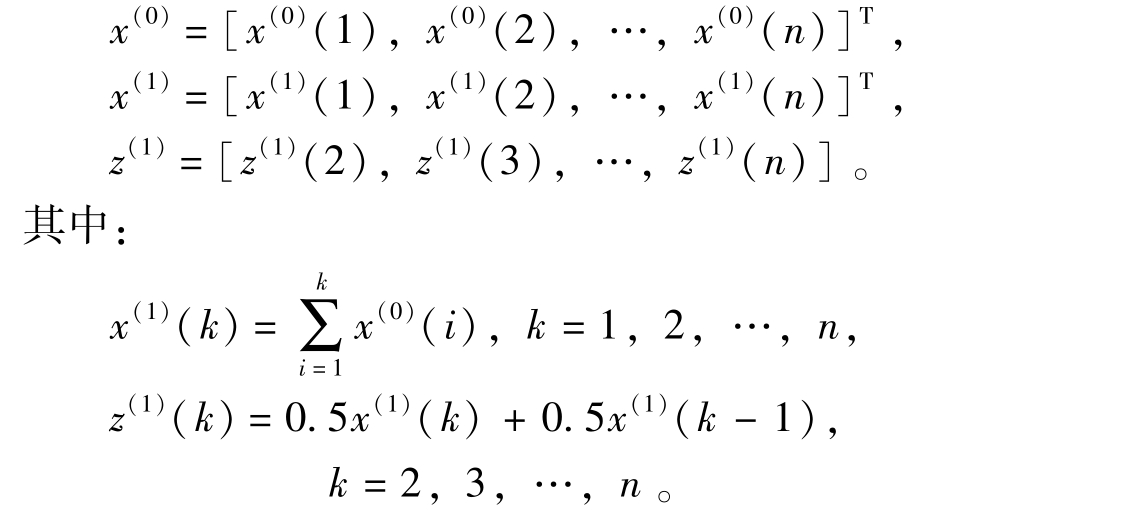
其中:a为发展系数,a的大小及符号反映x(0)和x(1)的发展态势;b为控制系数,具有灰信息覆盖的作用;z(1)为背景值序列。
利用最小二乘法计算a和b的估计值。
引入矩阵向量记号:
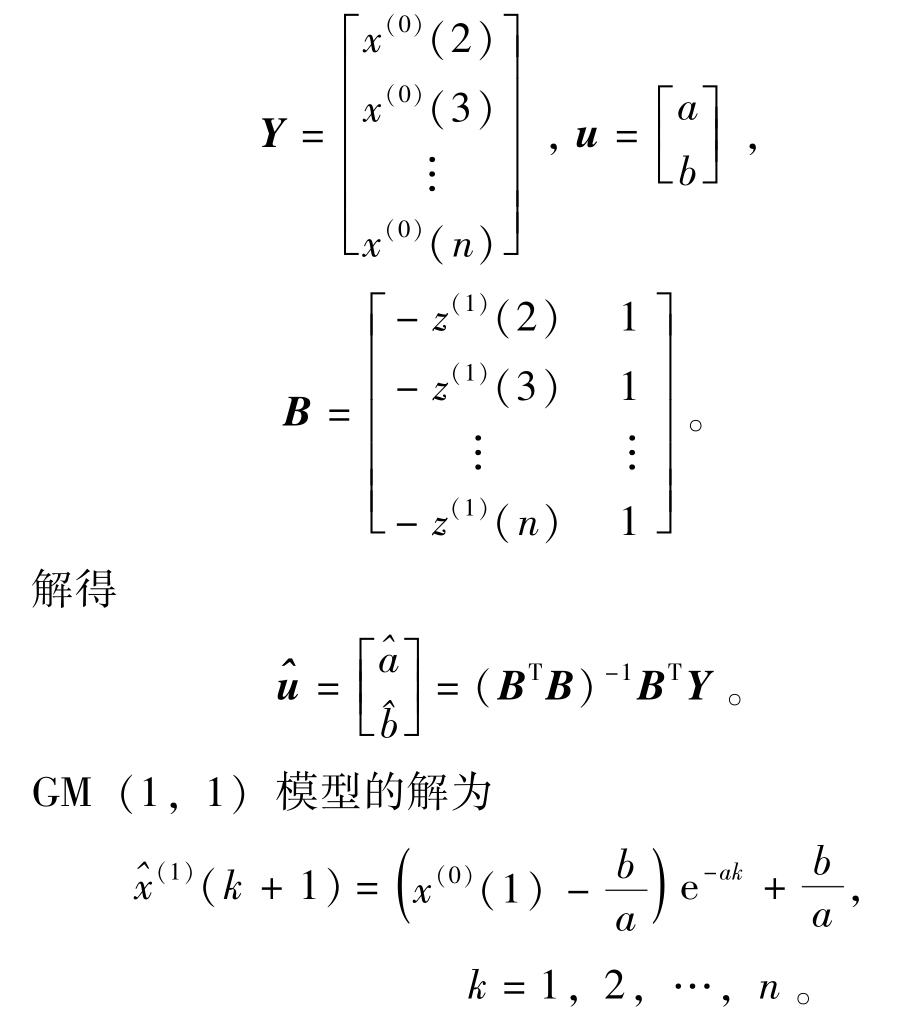
为保证GM(1,1)建模方法的可行性,需要对已知数据做必要的检验处理。计算x(0)数据序列的级比:
如果所有的级比都落在可容覆盖区间![]()
![]() 内,则数据序列x(0)可以建立GM(1,1)模型且可以进行灰色预测。
内,则数据序列x(0)可以建立GM(1,1)模型且可以进行灰色预测。
本研究中对预测模型精度的检验采用残差检验[6]。
线性内插法是根据一组已知的未知函数自变量的值和它相对应的函数值,利用等比关系去求未知函数其他值的近似计算方法[8-11]。
线性内插法是指两个量之间如果存在线性关系,如A(x1,y1)、B(x2,y2)为一条直线上的两个点,已知另一点P的x值,则利用它们的线性关系即可求得P点的对应值y。计算公式为
本研究中选用文献[4]中的数据,试验设4个生物功能群组合,即降油细菌组(B)、沙蚕+降油细菌组(NB)、翅碱蓬+降油细菌组(SB)、沙蚕+翅碱蓬+降油细菌组(NSB),另设一个空白对照组(C),通过线性变换,获得不同生物功能群组合土壤石油降解率随时间变化的数据,结果如表1所示。鉴于观测数据样本小且观测时间存在局部非等时距的特点,本研究中采用灰色预测模型和线性内插法相结合建立生物修复降解率预测模型。
表1 不同生物功能群组合土壤石油降解率随时间的变化
Tab.1 Changes in oil degradation rates in soil containing different biological functional groups

组合降解率degradation rate/% combination 15 d 30 d 45 d 60 d 70 d C 2.67 6.28 10.03 12.96 14.70 B 7.87 22.04 28.89 31.92 32.78 NB 9.35 24.97 29.74 33.83 36.16 SB 11.31 27.39 32.46 34.94 36.97 NSB 13.26 30.38 41.17 47.52 51.91
由于数据观测时间分别为15、30、45、60、70 d,前4个时间间隔相同,选择15、30、45、60 d试验数据利用灰色预测模型进行建模。
(1)级比检验。各组数据的级比为

每组数据均包含在(e-2,e2)中,且每组的第2、3个数据均包含在(0.716 531,1.395 612)中,故上述各组数据可用于GM(1,1)建模。
(2)建立决策模型。各组原始数据序列可利用GM(1,1)模型建模,具体生物修复降解率灰色预测模型详见表2。
(3)预测结果。对表1中数据15、30、45、60 d对应的部分数据序列利用(2)中GM(1,1)模型进行计算,对应70 d的数据在GM(1,1)模型的基础上结合线性内插法进行计算,这样就可得到各组数据序列的预测值。具体结果比较见表3。
(4)决策模型预测精度的比较。对本研究中提出的决策模型与线性回归模型在预测精度上进行比较,表4列出了各模型预测的相对误差。
(5)结果分析。从表3可见,对于5种组合的预测精度均在95%左右,表明本研究中提出的灰色预测模型与线性内插法结合的预测模型是可行的。同时,通过对本研究中提出的辅助决策模型和线性回归模型进行预测精度比较分析,从表4可以发现,本研究中提出的辅助决策模型的预测精度明显高于线性回归模型,很好地解决了生物修复试验降解率数据呈现局部数据序列非等时距数据序列的建模问题。
表2 各组合生物修复降解率的灰色预测模型
Tab.2 Grey prediction models for bioremediation degradation rates of various biological combinations
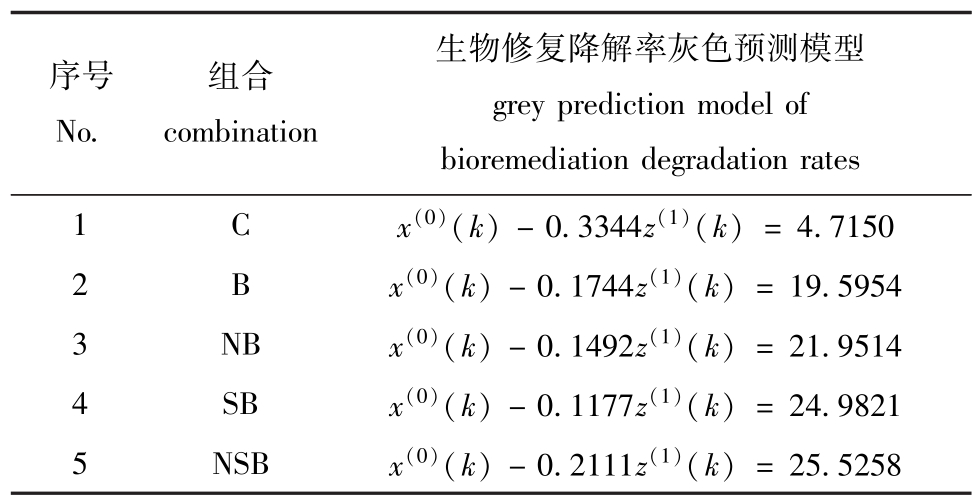
序号No.生物修复降解率灰色预测模型grey prediction model of bioremediation degradation rates 1 C x(0)(k)-0.3344z(1)(k)=组合combination 4.7150 2 B x(0)(k)-0.1744z(1)(k)=19.5954 3 NB x(0)(k)-0.1492z(1)(k)=21.9514 4 SB x(0)(k)-0.1177z(1)(k)=24.9821 5 NSB x(0)(k)-0.2111z(1)(k)=25.5258
表3 C、B、NB、SB、NSB组合实测值与预测值的比较分析
Tab.3 Com parative analysis ofmeasured and predicted values in groups C,B,NB,SB and NSB
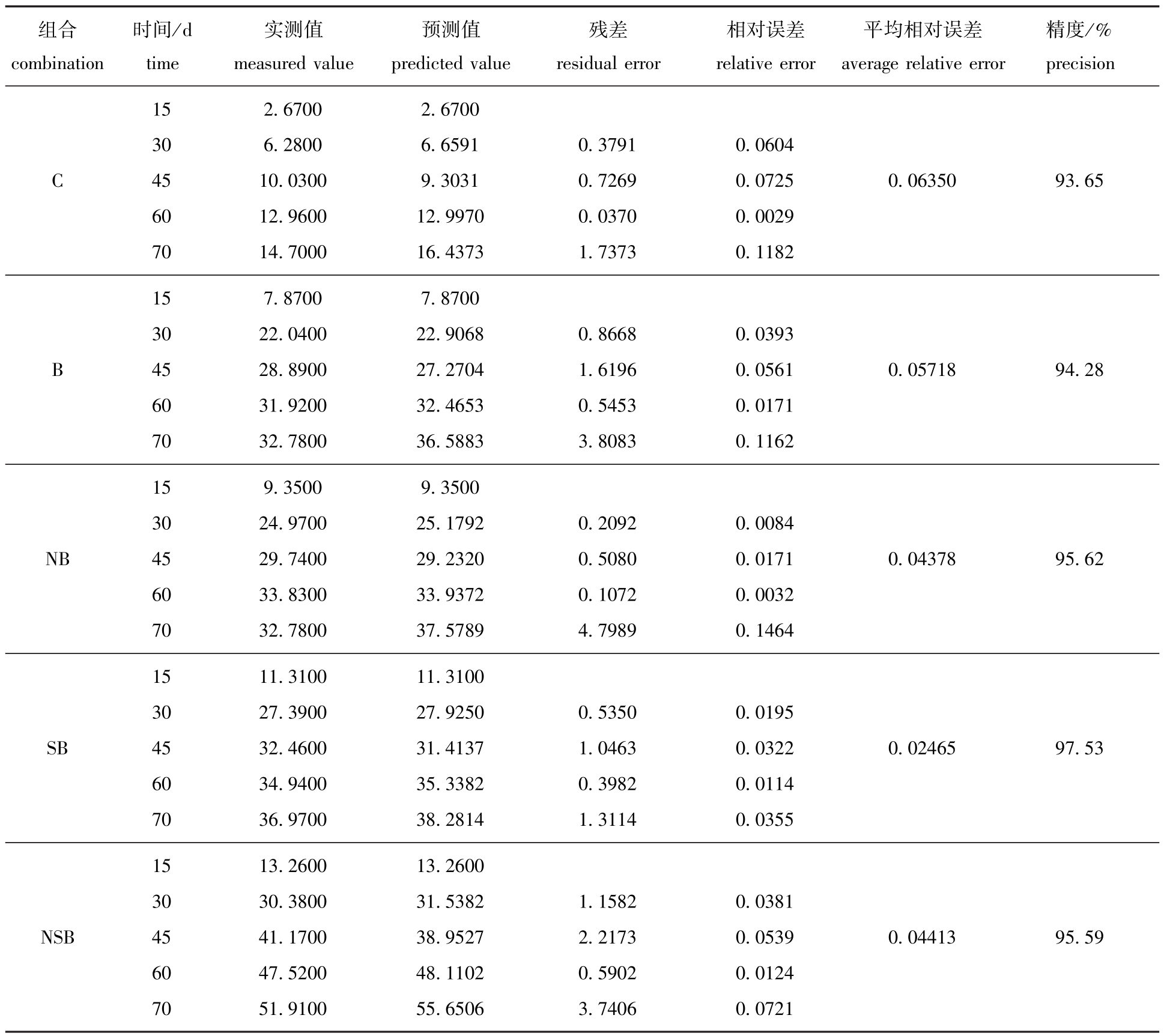
组合combination时间/d time实测值measured value预测值predicted value残差residual error相对误差relative error平均相对误差average relative error精度/% precision C 15 30 45 60 70 2.6700 6.2800 10.0300 12.9600 14.7000 2.6700 6.6591 9.3031 12.9970 16.4373 0.3791 0.7269 0.0370 1.7373 0.0604 0.0725 0.0029 0.1182 0.06350 93.65 B 15 30 45 60 70 7.8700 22.0400 28.8900 31.9200 32.7800 7.8700 22.9068 27.2704 32.4653 36.5883 0.8668 1.6196 0.5453 3.8083 0.0393 0.0561 0.0171 0.1162 0.05718 94.28 NB 15 30 45 60 70 9.3500 24.9700 29.7400 33.8300 32.7800 9.3500 25.1792 29.2320 33.9372 37.5789 0.2092 0.5080 0.1072 4.7989 0.0084 0.0171 0.0032 0.1464 0.04378 95.62 SB 15 30 45 60 70 11.3100 27.3900 32.4600 34.9400 36.9700 11.3100 27.9250 31.4137 35.3382 38.2814 0.5350 1.0463 0.3982 1.3114 0.0195 0.0322 0.0114 0.0355 0.02465 97.53 NSB 15 30 45 60 70 13.2600 30.3800 41.1700 47.5200 51.9100 13.2600 31.5382 38.9527 48.1102 55.6506 1.1582 2.2173 0.5902 3.7406 0.0381 0.0539 0.0124 0.0721 0.04413 95.59
本研究中根据生物修复试验数据特点提出了基于灰色预测模型与线性内插法相结合的溢油灾后生物修复降解率辅助决策模型的建模方法,并进行了实证研究,预测精度均在95%左右,体现了较好的吻合度。研究表明,本研究中提出的基于灰色预测模型与线性内插法相结合的建模方法可以有效地解决局部数据序列非等时距的建模问题,且预测结果具有科学性和准确性,可以应用于溢油污染事故后续修复和渔业生产恢复辅助决策系统的生物修复降解率辅助决策模型的建立,为溢油灾后修复和渔业生产恢复进行中长期决策提供辅助支持。
表4 本文提出的模型与线性回归模型的预测精度比较
Tab.4 Comparison of prediction accuracy of the model and linear regression model in present paper%
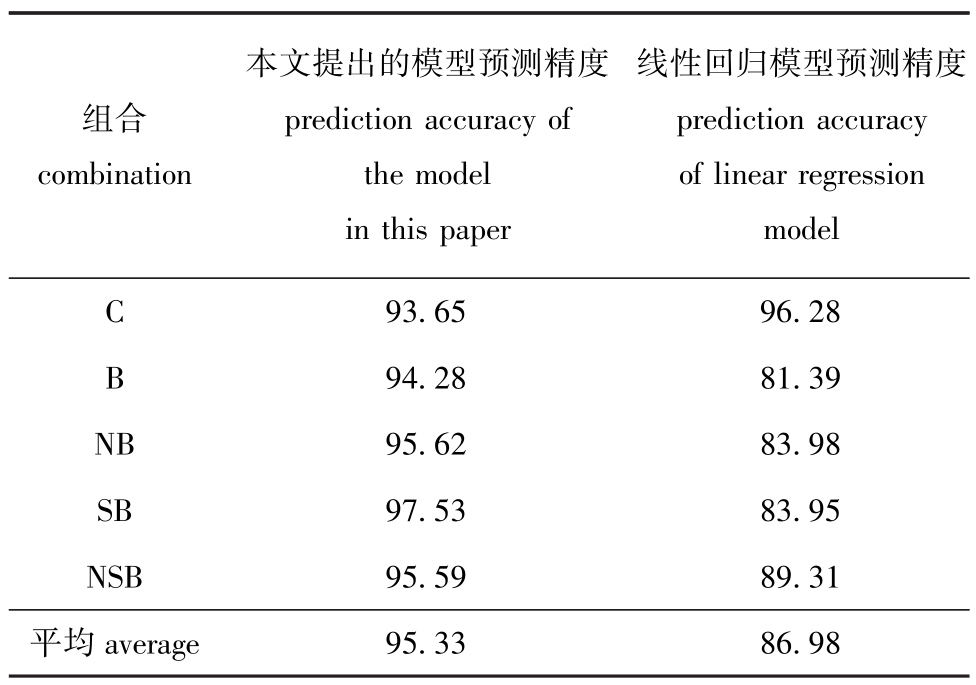
组合combination本文提出的模型预测精度prediction accuracy of themodel in this paper线性回归模型预测精度prediction accuracy of linear regression model 93.65 96.28 B 94.28 81.39 NB 95.62 83.98 SB 97.53 83.95 NSB 95.59 89.31平均C average 95.33 86.98
参考文献:
[1] 沈伟航,朱能武,王华金,等.石油污染土壤生物修复过程中毒性的植物指示[J].农业环境科学学报,2015,34(1):22-28.
[2] 朱文英,唐景春.小麦秸秆生物炭对石油烃污染土壤的修复作用[J].农业资源与环境学报,2014,31(3):259-264.
[3] 何洁,吉志新,王庆芝,等.翅碱蓬栽培对原油污染土壤理化性质的影响[J].大连海洋大学学报,2016,31(2):75-79.
[4] 樊鑫.基于沙蚕多功能群匹配的湿地微宇宙对石油烃去除效果研究[D].大连:大连海洋大学,2015.
[5] 康凯璇,兰秀茹,付娜,等.生物技术在石油污染修复领域的最新进展[J].石油化工安全环保技术,2015,31(5):71-75.
[6] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002:210-218.
[7] 刘思峰,方志耕,谢乃明,等.管理科学与工程新理论、新方法[M]//中国科学技术协会.2007~2008年管理科学与工程学科发展报告.北京:中国科学技术出版社,2008:31-52.
[8] 张惠民.中国古代历法中内插法的应用与发展[J].西南师范大学学报:自然科学版,2003,28(2):198-202.
[9] 张丽梅,宛立,董建新.细分外推与模糊预测在近海水质非线性时序处理中的比较分析[J].大连海洋大学学报,2015,30(3):324-329.
[10] 夏文香,林海涛,张英,等.海上溢油的污染控制技术[J].青岛建筑工程学院学报,2004,25(1):54-57.
[11] 缪新颖,葛廷友,高辉,等.基于神经网络和遗传算法的池塘溶解氧预测模型[J].大连海洋大学学报,2011,26(3):264-267.
Aided decision-making model of post-disaster bioremediation degradation rates for oil spills based on grey model and linear interpolation
Abstract:An aided decision-makingmodelwas established for post-disaster bioremediation degradation rates from oil spills by amathematicalmethod based on the combination of grey prediction theory with linear interpolation to develop aided decision-making system of post-disaster remediation and fishery production recovery after oil spills. The results showed that the prediction model had predicted accuracy range from 93.65%to 97.53%,indicating that themodel is feasible due to the fact that themodelingmethod combining the grey prediction theory and linear interpolation dealt effectively with the modeling problems with locally non-isochronous data sequences.The proposed model was shown tomeet the requirement for establishment of bioremediation aided decision model of degradation rate and to provide auxiliary support formedium and long-term decisions for post-disaster remediation and recovery of fishery production from oil spills.
Key words:greymodel;linear interpolation;bioremediation;degradation rate;decision-makingmodel
中图分类号:X55;O29
文献标志码:A
DOI:10.16535/j.cnki.dlhyxb.2016.05.017
文章编号:2095-1388(2016)05-0572-04
收稿日期:2016-05-14
基金项目:国家海洋公益性行业科研专项(201305002)