摘要:为研究西非沿海不同季节海洋环境因素对欧洲沙丁鱼Sardina pilchardus渔场形成的影响,基于Logistic模型,利用2007—2011年中国渔船在西非沿海捕捞欧洲沙丁鱼的渔业数据和网络获取的海洋环境遥感数据 [包括海表温度 (SST)、叶绿素a浓度 (Chl)和海面高度异常 (SSHA)],构建了春、夏、秋、冬4个季节欧洲沙丁鱼渔场与环境因素关系的模型,利用逐步回归法对自变量进行筛选,并对最优回归模型进行评价,最后利用该模型对4个季节影响欧洲沙丁鱼出现的各个环境要素进行了分析。结果表明,4个季节欧洲沙丁鱼的出现与地理位置有着密切的关系,而在4个季节中环境因素对欧洲沙丁鱼出现有着不同的作用,即春季影响欧洲沙丁鱼出现的显著因子为SST和SSHA,夏季为Chl和SSHA,秋季为SST,冬季则为SSHA。该研究结果对欧洲沙丁鱼渔场形成机制分析具有一定的应用价值。
关键词:欧洲沙丁鱼;西非沿海;Logistic回归模型;渔场
欧洲沙丁鱼Sardina pilchardus广泛分布于大西洋的西非沿岸以及地中海、英吉利海峡等海域。欧洲沙丁鱼属中上层暖水性鱼类,同其他海洋中上层鱼类一样,也具有集群和洄游的习性。在西非沿岸海域上升流的驱动下,大量丰富的营养盐被输送至海面,使饵料生物大量繁殖,从而形成优良渔场。非洲西北沿岸的大西洋海域欧洲沙丁鱼分为3个种群,由北向南依次为北部种群 (Cape Cantin至Gibraltar Strait)、中部种群 (Cape Cantin至Cape Bojador)和南部种群 (Cape Bojador以南)[1]。其中南部种群分布有较大的波动,最远可达到塞内加尔[2]。
国内外学者对欧洲沙丁鱼的研究多集中在基础生物学方面,包括不同海域的形态学差异、沙丁鱼耳石与生长的关系等[3-5]。在环境变化对欧洲沙丁鱼渔业资源的影响方面,诸多物理和生物要素,包括近海埃克曼输送、海表温度、浮游生物等均对其资源变动起到了重要作用[6-7],但此方面的研究多数是从欧洲沙丁鱼的年际变化展开,以探寻其在不同年份的集群和洄游规律,而对其在不同季节与环境因素相关关系的研究则相对较少。另外,上述研究多集中在20°N以北的非洲沿岸和地中海等海域[1,3-4,8],对于中东大西洋20°N以南海域很少涉及。本研究中,利用2007—2011年中国渔船在非洲西部沿海捕捞欧洲沙丁鱼的渔业数据,采用Logistic回归模型分析了不同季节主要海洋环境因素与地理位置对欧洲沙丁鱼分布的影响,并对不同季节各个环境和空间要素的影响规律进行了探讨,以期为该海域欧洲沙丁鱼渔场形成机制的研究和渔情预报工作提供参考。
1.1 数据来源
环境数据包括 2007—2011年海表温度(SST)、叶绿素a浓度 (Chl)的日平均数据 (空间分辨率为9 km)由网站http://oceancolor.gsfc. nasa.gov/下载获得。海面高度异常 (SSHA)数据(空间分辨率为0.25°,时间分辨率为周)由AVISO网站 (http://www.aviso.altimetry.fr/)提供,通过Python开源软件包Marine Geospatial Ecology-Tools(MGET),借助ArcGIS工具箱ArcToolbox下载获得。
渔业数据主要来自2007—2011年中国渔船在非洲毛里塔尼亚沿岸的欧洲沙丁鱼捕捞记录,主要包括日期、经纬度、欧洲沙丁鱼产量和投网次数。
根据渔获数据范围,确定环境数据的空间范围为15.9°W~18.5°W、16.9°N~21°N。用取平均值的方法,将海表温度、叶绿素a浓度数据和渔业数据分别抽取成0.1°×0.1°的格点数据。海面高度异常数据经插值后,同样生成时间分辨率为天、空间分辨率为0.1°×0.1°的格点数据。同时计算欧洲沙丁鱼各个格点 (0.1°×0.1°)的单位捕捞努力量渔获量 (CPUE,kg/网):
其中:C为某个格点内一天的总产量 (kg);N为该格点内一天的总网次。CPUE数据与上述环境数据按时间和空间位置匹配,得到有效记录1832条。
1.2 方法
1.2.1 季节划分 沙丁鱼是一种具有较强季节性洄游特点的中上层鱼类,春、夏季生活在近岸海域,秋、冬季水温较低时,洄游到水温较高的深海海域[1,4,9]。根据沙丁鱼的这一生物学特征,同时依据天文学季节划分法,将上述环境与渔获记录划分为春、夏、秋、冬4个季节,即3月21日至6 月20日为春季,6月21日至9月21日为夏季,9 月22日至12月21日为秋季,12月22日至翌年3 月20日为冬季。
按上述方法划分季节后,由于不同季节捕捞范围和生产区域大小有所不同,各个季节在该研究海域的作业分布情况如图1所示。
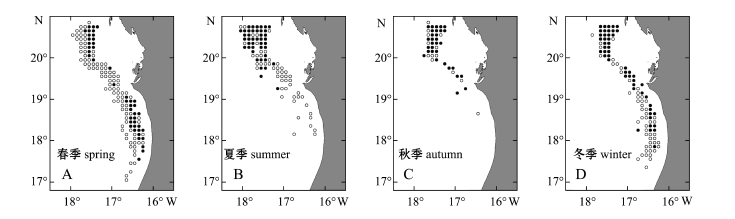
注:其中实心黑点为产量大于0的渔区;空心点为产量等于0的渔区
Note:The bold circles denote the fishing ground with catch>0 and open ones denote the fishing ground with catch=0
图1 欧洲沙丁鱼在不同季节的作业位置
Fig.1 Fishing positions of sard ine Sardina pilchardus in different seasons
1.2.2 模型的确定
(1)环境变量的选取和回归模型的建立。有研究表明,欧洲沙丁鱼的出现位置除了与地理位置有关外,还与所在海域的海表温度、叶绿素a浓度和埃克曼输送等环境因素密切联系[1-2,9]。其中,由风生海流产生的埃克曼输送常被视为影响欧洲沙丁鱼资源的重要因素,但其数值需通过风速计算得到[1,6],从而增加了分析过程的复杂性。Susanto等[10]研究表明,埃克曼输送可引起海平面的变化。Cheng等[11]研究表明,海面高度在某种程度上也可以反映上升流的强弱和位置。基于这两方面的原因,本研究中未使用埃克曼输送,而是代之以海面高度异常 (SSHA)作为研究的环境指标之一,因此,在建立分析模型时,将海表温度SST、叶绿素a浓度Chl、海面高度异常SSHA、经度Lon和纬度Lat这5个变量作为自变量。另一方面,以往的研究中常将CPUE作为模型的因变量,来反映资源的状况和丰度[12]。但对欧洲沙丁鱼渔获数据资料的初步分析发现,CPUE为0值的记录达1148条,占总记录数的62.7%,且分布的偏度达1.452,呈现严重的偏态分布。一般的多元回归方程假设因变量为正态分布,但本研究中的CPUE分布不满足这一假设,而Logistic回归模型对正态性和方差齐性均不做要求[13]。因此,在本研究中用因变量y来表示欧洲沙丁鱼是否出现,即y=0表示格点CPUE等于0,y=1表示CPUE大于0,则该回归模型的Logistic函数形式为
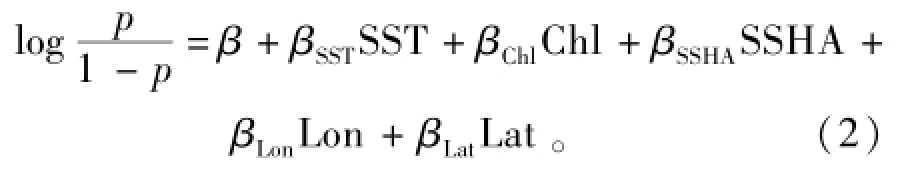
其中:β为常数项;β(…)为相应环境变量和空间变量系数;p为欧洲沙丁鱼出现发生的概率,定义为
经检验,4个季节解释变量的方差膨胀因子(VIF)均小于10(表1),表示模型不存在多重共线性[14],因此,可以满足Logistic回归模型的假设条件。
表1 模型中释放变量的方差膨胀因子 (VIF)
Tab.1 Variance inflation factor(VIF)of explanatory variables in themodel
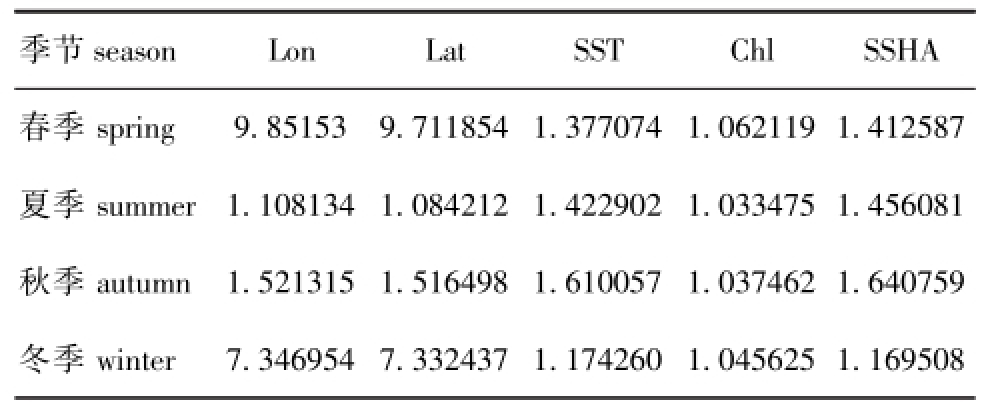
季节season Lon Lat SST Chl SSHA春季spring 9.85153 9.711854 1.377074 1.062119 1. .169508 412587夏季summer 1.108134 1.084212 1.422902 1.033475 1.456081秋季autumn 1.521315 1.516498 1.610057 1.037462 1.640759冬季winter 7.346954 7.332437 1.174260 1.045625 1
与一般多元线性回归利用最小二乘法 (OLS)求得环境变量系数方法不同,Logistic回归通常采用最大似然估计法 (maximum likelihood estimate,MLE)估算各个回归系数[14]。
实际应用中,回归方程有些自变量对因变量y有作用,但有些自变量在回归方程中无足轻重,这时将它们留在回归方程中,不但增加计算上的复杂程度,而且不能保证有好的回归效果。为了克服这些缺点,利用逐步回归方法[15-16],通过比较 AIC (akaike information criterion)值,去除对因变量影响不显著的自变量,获得最优回归方程。
(2)模型回归指标评价。拟合优度度量是模型中衡量预测值和观测值之间总体是否一致性的重要指标。Hosmer Lemeshow拟合优度指标 (通常简写为H-L),是由Hosmer和Lemeshow在1989年提出的一种Logistic模型拟合优度检验的方法[17]。其对应的零假设H0表示预测值概率和观测值之间无显著性差异,即当H-L检验值到达某个显著水平时,表示拟合优度良好。另外,Wald检验是用于回归系数是否显著的判断标准,即检验自变量对因变量是否有显著影响,它是对整体回归系数是否显著的检验。
(3)模型精度检验[18]。ROC (receiver operating characteristic)曲线将某种试验的灵敏度与特异性相结合,是一种全面科学评价检测项目的方法。当模型建立后,可以通过环境和空间值来计算欧洲沙丁鱼出现的概率p(0<p<1)。设有阈值a(0<a<1),当p>a时,表示该鱼种会出现,即y=1,否则y=0。依此方法,与相应时间和位置的实际渔获对比,就可以计算出一个真阳性率 (TPR)和假阳性率 (FPR,即1-specificity)的组合。取不同的a值,就得到多组数据点。将FPR和TPR分别作为X轴和Y轴,连接所有的数据点,就得到了一条ROC曲线。当ROC曲线下面积 (area under the curve,AUC)接近0.5时,预报无意义;当AUC<0.7时,预报准确率较低;当AUC=0.7~0.9时,预报准确率中等;当AUC>0.9时,预报准确率较高。以此方法可对模型的精度进行检验。另外,ROC曲线上最靠近坐标图左上方的点为敏感性和特异性均较高的临界值 (cut-off值),为logit函数中参数p的阈值点,可作为判断是否为渔场渔区的最佳概率值。
2.1 模型系数的估算
首先保留所有变量 (3个环境变量和2个空间位置变量),利用Logistic模型公式 (2)估算所有系数值。从初步回归结果看,春季Chl、夏季SST、秋季Chl和SSHA、冬季SST和Chl的回归系数均未通过0.1显著性水平检验,故采用逐步回归方法,重新筛选解释变量,得到结果如表2所示。
表2 不同季节的Logistic回归模型
Tab.2 Logistics regression models in each season

季节season回归模型3.54865Lon+2.28635Lat夏季summer regression model春季spring log p 1-p=10.7345+0.16500SST-0.07124SSHA+ p=-22.68268-0.03182Chl-0.17074SSHA+ 1.04654Lat秋季autumn log p 1-3.28314Lat p=-5.88923-0.17610SST+1.45213Lon+ 1.71834Lat冬季winter log p 1-log p 1-p=8.20440+0.03801SSHA+4.28217Lon+
2.2 回归模型指标的评价
2.2.1 拟合优度 经H-L检验,4个季节的P值均大于0.1(表3),说明在0.1检验水平下不能拒绝关于模型拟合数据很好的假设,即模型的拟合度均较好。
2.2.2 回归系数检验 经Wald检验,各个季节的P值均远小于0.01(表4),即模型的整体回归系数显著。
用Z检验分别检验模型中各个系数的显著性,结果表明,4个季节中除常数项外,各个解释变量系数的Z检验P值均小于0.1(表5),表明各个回归系数在0.1检验水平上均为显著。
表3 H-L拟合优度的检验结果
Tab.3 Result of H-L goodness in a fit test
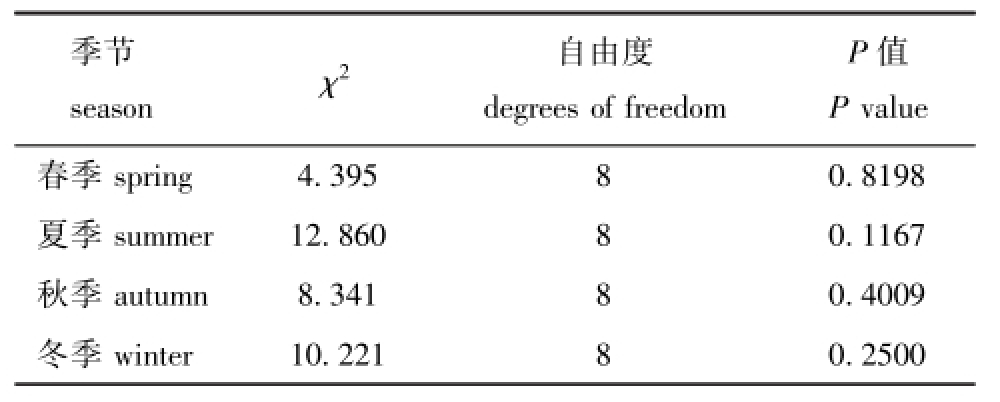
季节season Χ2 自由度degrees of freedom P值P value春季spring 4.395 8 0.8198夏季summer 12.860 8 0.1167秋季autumn 8.341 8 0.4009冬季winter 10.221 8 0.2500
表4 回归系数显著性的W ald检验结果
Tab.4 Result of parametric test statistic in aW ald test
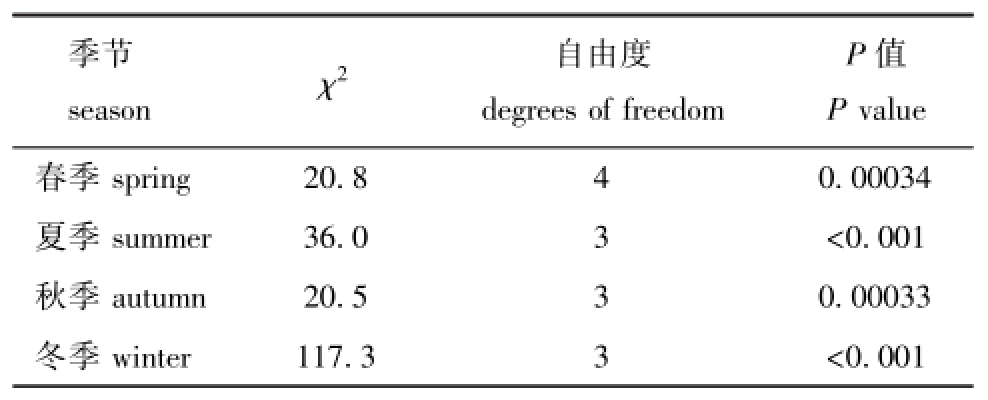
Χ2 自由度degrees of freedom P值P季节season value春季spring 20.8 4 0.00034夏季summer 36.0 3 <0.001秋季autumn 20.5 3 0.00033冬季winter 117.3 3 <0.001
表5 各个回归系数的Z检验结果
Tab.5 Parametric test statistics of Z test results
注:*表示有显著性差异 (P<0.05);**表示有极显著性差异 (P<0.01)
Note:*means significant difference(P<0.05);**means very significant difference(P<0.01)
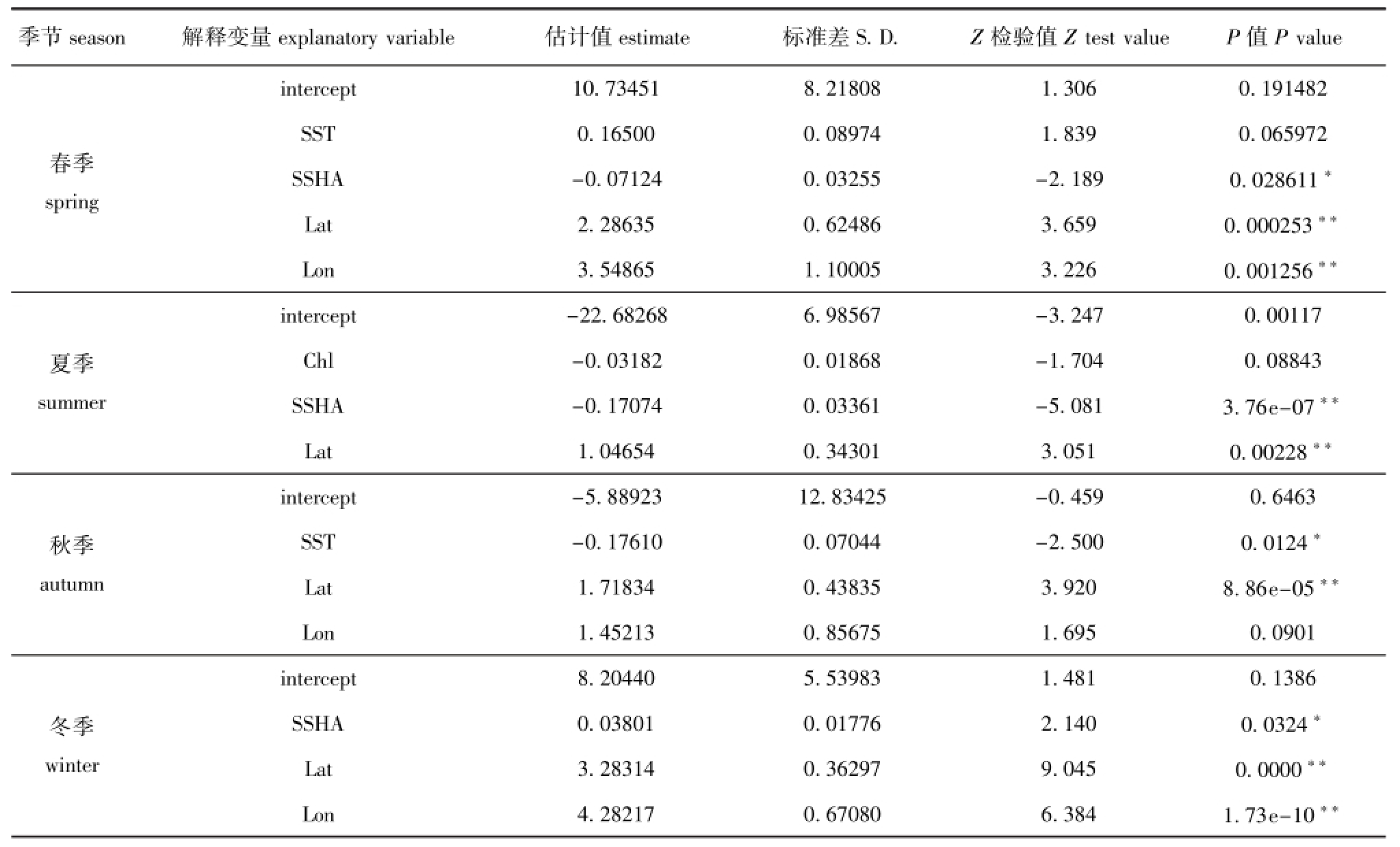
季节season 解释变量explanatory variable 估计值estimate 标准差S.D. Z检验值Z test value P值P value春季spring intercept 10.73451 8.21808 1.306 0.191482 SST 0.16500 0.08974 1.839 0.065972 SSHA -0.07124 0.03255 -2.189 0.028611*Lat 2.28635 0.62486 3.659 0.000253**Lon 3.54865 1.10005 3.226 0.001256**夏季summer intercept -22.68268 6.98567 -3.247 0.00117 Chl -0.03182 0.01868 -1.704 0.08843 SSHA -0.17074 0.03361 -5.081 3.76e-07**Lat 1.04654 0.34301 3.051 0.00228**秋季autumn intercept -5.88923 12.83425 -0.459 0.6463 SST -0.17610 0.07044 -2.500 0.0124*Lat 1.71834 0.43835 3.920 8.86e-05**Lon 1.45213 0.85675 1.695 0.0901冬季winter intercept 8.20440 5.53983 1.481 0.1386 SSHA 0.03801 0.01776 2.140 0.0324*Lat 3.28314 0.36297 9.045 0.0000**Lon 4.28217 0.67080 6.384 1.73e-10**
2.2.3 模型的ROC检验 ROC检验结果表明,春季、夏季和冬季的AUC均为0.7~0.9,达到了中等预报精度,秋季AUC也近似等于0.7,也接近中等的预报精度,各图中ROC曲线上的黑点为cut-off值 (图2)。
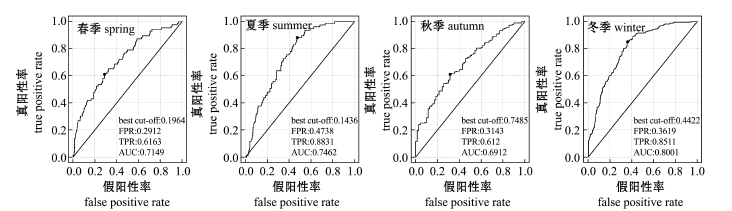
图2 4个季节模型的ROC曲线检验结果
Fig.2 Receiver operating characteristic(ROC)test result ofmodels in 4 seasons
3.1 影响欧洲沙丁鱼分布的环境因素分析
Logistic模型的回归结果表明,在不同季节,空间与环境因子影响沙丁鱼出现的强弱程度是不同的,模型中各个因子系数的显著性也有所不同。
从4个季节的Logistic模型看,地理位置均为影响沙丁鱼分布的主要因素,其中纬度对该鱼种的影响在4个季度中均显著,说明该鱼种分布与地理位置相关性较强。模型中纬度变量的系数均为正值,表明该海域沙丁鱼出现的概率大小有由南至北逐渐增强的趋势。经度系数亦为正值,表明该鱼种出现机率由沿岸向外海逐步减少。与以往研究相比,本研究中所涉及的渔场位于非洲沿岸3个渔场的南部边缘,因此,模型中纬度变量的系数符号为正具有合理性。另外,在北大西洋西北沿岸信风作用下,形成了东边界上升流。在20°N~30°N,全年最强的信风发生在7—8月[19],而在20°N以南,上升流期发生在春、冬季[7]。Kifani[1]研究表明,在非洲西北沿岸海域的非上升流季节,欧洲沙丁鱼的分布更集中,而在上升流季节,其分布更加分散。本研究中,夏季和秋季非上升流季节欧洲沙丁鱼主要聚集在19°N以北海域,冬季和春季沿海岸线向南延伸 (图1),这与Kifani[1]的研究结论基本一致,但其分布在经度上并没有向外海拓展。由CPUE的春、冬季分布图 (图3~图5)可知,该鱼种在作业区域的西部边缘很少出现,且渔获区域与环境要素等值线分布较一致,由此推断,西部外海未出现渔场的原因,应为该鱼种受自身生物特性和外界环境共同作用所致,而并非渔船作业区域限制造成。从模型结果分析可见,夏、秋两季经度变量系数的显著性表现为不显著 (夏季)和边缘显著,说明欧洲沙丁鱼在这两个季节中,在经度上出现的规律性并不明显。
在环境因素方面,SST的变化与包括海流的水平输送、表层热量的吸收、上升流和水团的混合变化等多种海洋过程密切相关[20]。有研究表明,欧洲沙丁鱼多栖息在SST范围为8~24℃的水域,常表现出偏好温暖的浅水水域习性[21-22]。本研究中的海域位于21°N以南,春、夏、秋、冬4个季节该鱼种出现的 SST范围分别为 15.2~26.5、14.7~20.4、14.6~24.3、13.6~26.6℃,与上述研究结果略有差异,可能与本研究较以前研究的海域位置更加偏南,从而导致水温更高有关。模型结果显示,春、秋两个季节的SST对沙丁鱼的出现有显著影响。从图3-A可见,春季由于信风强劲,沿岸海域处于强上升流期间,水温处于较低水平,温度变量的系数为正,说明沙丁鱼更趋向聚集于上升流外侧较高水温处;而秋季处于上升流逐渐形成时期,水温较低的上升流区往往是饵料丰富的区域,沙丁鱼更趋于向上升流中心处聚集,因此,模型中的SST系数表现为负值。
在叶绿素方面,Nehring等[8]研究发现,在大西洋东北沿岸的博哈多尔角 (Cape Bojador)和巴巴斯角 (Cape Barbas)之间的海域,叶绿素 a浓度与沙丁鱼种群总资源量和拖网日产量之间存在着较好的相关性,当初级生产力增加时,通常会形成好的渔场。Krzeptowski[23]报道,沙丁鱼摄食最活跃期为5—10月,Bravo de Laguna等[24]认为,沙丁鱼摄食率在夏季 (7—8月)为高峰期,可达0.83~0.88,而在冬季 (1—3月)只有 0.65~0.70。以上研究中沙丁鱼摄食活跃期与本研究中夏季 (6月20日—9月20日)的时间范围基本重合,逐步回归后的夏季Logistic模型中也存在叶绿素因子,说明叶绿素也是主要的影响因数之一。但Bravo de Laguna等[24]也指出,沙丁鱼的季节饵料组成随水文条件而变化。在上升流剧烈的时期,饵料组成以浮游植物为主,而在上升流微弱的时期,饵料组成以浮游动物为主,由此推断,夏季浮游植物并不是沙丁鱼的直接饵料来源。大多数研究表明,叶绿素浓度与浮游动物丰度之间存在正相关[25],这似乎与本模型中叶绿素系数符号为负值相矛盾。但浮游植物与浮游动物之间存在复杂的关系[26]。也有部分研究表明,在7—9月 (夏季),北大西洋叶绿素a浓度与某些浮游动物丰度之间存在负相关关系[27]。因此,夏季叶绿素浓度对沙丁鱼CPUE的影响机制有待进一步研究。
海面高度异常可以体现海水的上层厚度(UTL),负的SSHA区域因其辐散流动模式,在北半球会形成气旋涡旋,常用来鉴别上升流区[11,28]。上升流将冷的富含营养盐的海水带上海面,以补充表层水,从而有利于形成沙丁鱼的饵料场。Ettahiri等[29]研究表明,沙丁鱼一般寻找上升流区中心区作为产卵场所。本研究的模型中,除秋季外,其他3个季节的SSHA系数均显著,表明SSHA对沙丁鱼分布有较大的影响。相对于夏、秋季为上升流较强的季节,春、冬季小于0的海面高度异常区域较大。春季和夏季SSHA的系数为负值,表明沙丁鱼有向低SSHA区域移动的倾向,对于春季来说,这正是上升流区的中心区;而对于夏季,沙丁鱼在此季节会向北部集中,该处也正是SSHA偏低的海域;冬季处于上升流逐渐增强的阶段,此时模型中SSHA系数为正值,说明沙丁鱼有向SSHA较高、SST相对也较高的海域移动的趋势,这可能与冬季上升流核心区域海水温度过低有关。
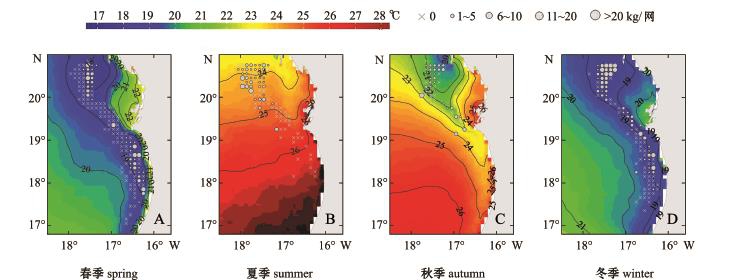
图3 中东大西洋沿岸4个季节的年平均SST分布图
Fig.3 Seasonal profile of average annual SST at Central-Eastern Atlan tic coast
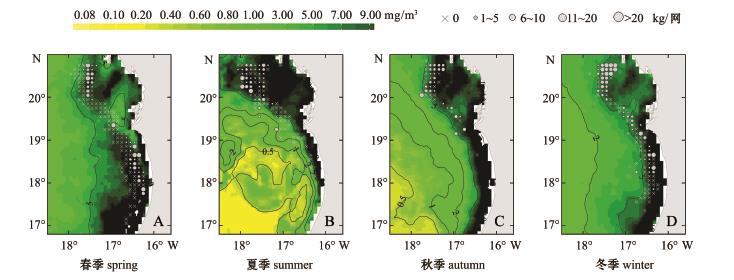
图4 中东大西洋沿岸4个季节的年平均叶绿素a浓度分布图
Fig.4 Seasonal profile of average annual Chl-a concentration at Central-Eastern Atlantic coast
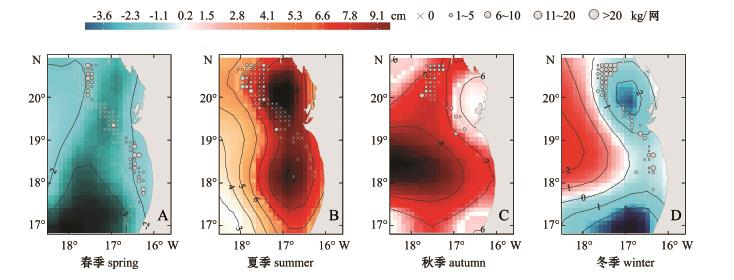
图5 中东大西洋沿岸4个季节的年平均海面高度异常分布图
Fig.5 Seasonal p rofile of average annual SSHA at Cen tral-Eastern Atlantic coast
3.2 模型仍存在的问题
由于渔业调查中客观条件的限制,采样数据出现零膨胀分布是经常遇到的情形。渔获信息虽然为连续数据,但分布往往呈严重偏态,不能满足传统的全局回归因变量正态分布的假设条件。通过对连续的渔获数据 (因变量)离散化为渔场的 “是”与 “非”,是解决这种问题一个简单有效的途径,也是通过机器学习进行渔场分析和预报的常用方法[30-31]。本研究中,利用Logistic模型对中东大西洋欧洲沙丁鱼渔场发生概率进行建模,其结果为一个0到1之间的概率值,特别适用于产生两个逻辑值 (如鱼群出现的 “是”与 “否”)的判断依据。但Logistic回归也存在一些缺点,如与某些回归模型 (如回归树)相比,它需要更多的假设 (如因变量y要服从二项分布或者多项式分布),并且对离群数据 (outlier)比较敏感。对连续分布的渔获数据而言,在应用Logistic回归时要进行强制的离散化 (转化成0和1),这一过程无疑会损失一部分渔获信息。
另外,从渔业资源的角度来看,欧洲沙丁鱼属于一种年际波动剧烈的鱼种[32]。本研究中为获取其季节性的渔场分布规律,对5年的渔业数据按季节进行了处理,这样虽然能挖掘出欧洲沙丁鱼在不同季节的环境与渔场变化规律,但也忽略了其年际变化特征,不利于分析相应环境因子年间变化对沙丁鱼集群的影响。因此,开展其年际变化规律的研究将是下一步的任务。
本研究中利用 Logistic回归法建立了2007—2011年4个季节欧洲沙丁鱼出现的概率与环境、空间要素的相关模型,估算了各个解释变量系数,并结合相关文献对不同季节影响欧洲沙丁鱼出现的情况进行了分析。结果表明,全年4个季节欧洲沙丁鱼的出现与地理位置有着密切关系,而在4个季节中不同环境因子对欧洲沙丁鱼的出现存在着不同的影响和作用,并究其原因进行了初步的探讨和分析。本研究结果为今后对该海域欧洲沙丁鱼渔场的进一步深入分析提供了一定的参考。
参考文献:
[1] Kifani S.Climate dependent fluctuations of the Moroccan sardine and their impact on fisheries[C]//Marie-Hélène D,Philippe C,Mendelssohn R,et al.Global Versus Local Changes in Upwelling Systems.Paris:ORSTOM,1998.
[2] Fréon P,Stéquert B.Note sur la présence de Sardina pilchardus (Walb.)au Sénégal:étude de la biométrie et interpretation[J]. Rapports et Procès-verbaux des Réunions du Conseil Internationale de l'Exploration de la Mer,1982,180:345-349.
[3] Silva A.Morphometric variation among sardine(Sardina pilchardus)populations from the northeastern Atlantic and the western Mediterranean[J].ICES Journal ofMarine Science,2003,60(6):1352-1360.
[4] 胡贯宇,叶旭昌,方舟,等.摩洛哥南部沿岸沙丁鱼耳石与生长的关系[J].海洋渔业,2014,36(2):123-130.
[5] Correia A T,Hamer P,Carocinho B,et al.Evidence for meta-population structure of Sardina pilchardus in the Atlantic Iberian waters from otolith elemental signatures of a strong cohort[J].Fisheries Research,2014,149:76-85.
[6] Guisande C,Vergara A R,Riveiro I,et al.Climate change and abundance of the Atlantic-Iberian sardine(Sardina pilchardus)[J].FisheriesOceanography,2004,13(2):91-101.
[7] Zeeberg J,Corten A,Tjoe-Awie P,et al.Climatemodulates the effects of Sardinella aurita fisheries off Northwest Africa[J].Fisheries Research,2008,89(1):65-75.
[8] Nehring D,Holzlohner S.Investigations on the relationship between environmental conditions and distribution of Sardina pilchardus in the shelfarea offNorthwestAfrica[J].RapportsetProcès-verbaux des Réunions du Conseil Internationale de l'Exp loration de la Mer,1982,180:342-344.
[9] Atarhouch T,Rüber L,Gonzalez E G,et al.Signature of an early genetic bottleneck in a population of Moroccan sardines(Sardina pilchardus)[J].Molecular Phylogenetics and Evolution,2006,39 (2):373-383.
[10] Susanto R D,Gordon A L,Sprintall J.Observations and proxies of the surface layer throughflow in Lombok Strait[J].Journal of Geophysical Research,2007,112(C3),doi:10.1029/2006JC00 3790.
[11] Cheng Y H,Ho C R,Zheng Zhewen,et al.An algorithm for cold patch detection in the Sea offnortheast Taiwan usingmulti-sensor data[J].Sensors,2009,9(7):5521-5533.
[12] Mendelssohn R,Cury P.Fluctuations of a fortnightly abundance index of the Ivoirian coastal pelagic species and associated environmental conditions[J].Canadian Journal of Fisheries and A-quatic Sciences,1987,44(2):408-421.
[13] 冯国双,陈景武,周春莲.Logistic回归应用中容易忽视的几个问题[J].中华流行病学杂志,2004,25(6):544-545.
[14] Hair Jr JF,Black W C,Babin B J,etal.Multivariate Data Analysis:A Global Perspective[M].7th ed.Upper Saddle River,NJ:Pearson Prentice Hall,2010.
[15] Hosmer DW,Lemeshow S.Applied Logistic Regression[M].2nd ed.New York:John Wiley,2000.
[16] Hocking R R.A biometrics invited paper:the analysis and selection of variables in linear regression[J].Biometrics,1976,32 (1):1-49.
[17] Draper N,Smith H.Applied Regression Analysis[M].2nd ed. New York:John Wiley&Sons,Inc,1981.
[18] Takahashi K,Uchiyama H,Yanagisawa S,et al.The logistic regression and ROC analysis of group-based screening for predicting diabetes incidence in four years[J].The Kobe Journal of Medical Sciences,2006,52(6):171-180.
[19] WoosterW S,Bakun A,McLain D R.The seasonal upwelling cycle along the eastern boundary of the North Atlantic[J].Journal of Marine Research,1976,34(2):131-141.
[20] Miller A J,Schneider N.Interdecadal climate regime dynamics in the North Pacific Ocean:theories,observations and ecosystem impacts[J].Progress in Oceanography,2000,47(2-4):355-379.
[21] Giannoulaki M,Machias A,Somarakis S,et al.The spatial distribution of anchovy and sardine in the northern Aegean Sea in relation to hydrographic regimes[J].Belgian Journal of Zoology,2005,135(2):151-156.
[22] Stratoudakis Y,Coombs S,Lago de Lanzós A,et al.Sardine(Sardina pilchardus)spawning seasonality in European waters of the northeast Atlantic[J].Marine Biology,2007,152(1):201-212.
[23] KrzeptowskiM.Biological characteristics of the sardine(Sardina pilchardus Walb.)offWest Sahara[J].Acta Ichthyologica et Piscatoria,1983,13(1):13-38.
[24] Bravo de Laguna J,Fernandez M A R,Santana JC.The Spanish fishery on sardine(Sardina pilchardus)off West Africa[R].Copenhagen:International Council for the Exp loration of the Sea (ICES),1976.
[25] Gowen R J,McCullough G,Dickey-Collas M,et al.Copepod abundance in the western Irish Sea:relationship to physical regime,phytoplankton production and standing stock[J].Journal of Plankton Research,1998,20(2):315-330.
[26] 陈长胜.海洋生态系统动力学与模型[M].北京:高等教育出版社,2003.
[27] Feng Jianfeng,Stige L C,Durant JM,et al.Large-scale seasondependent effects of temperature and zooplankton on phytoplankton in the North Atlantic[J].Marina Ecology Progress Series,2014,502:25-37.
[28] Lin Chunyi,Ho C R,Zheng Zhewen,et al.Validation and variation of upper layer thickness in South China Sea from satellite altimeter data[J].Sensors,2008,8(6):3802-3818.
[29] Ettahiri O,Berraho A,Vidy G,et al.Observation on the spawning of Sardina and Sardinella off the south Moroccan Atlantic coast (21-26°N)[J].Fisheries Research,2003,60(2-3):207-222.
[30] Windle M J S,Rose G A,Devillers R,et al.Exp loring spatial non-stationarity of fisheries survey data using geographically weighted regression(GWR):an example from the Northwest Atlantic[J].ICES Journal of Marine Science,2010,67(1):145-154.
[31] 崔雪森,伍玉梅,张晶,等.基于分类回归树算法的东南太平洋智利竹筴鱼渔场预报[J].中国海洋大学学报,2012,42(7-8):53-59.
[32] FAO:Global Capture Production 1950-2013[EB/OL].[2015-01-20].http://www.fao.org/fishery/statistics/global-captureproduction/query/en.
A Logistic regression model on relationship between sardine Sardina pilchardus fishing ground and environmental variables in the coastalwaters of W est Africa
Abstract:In the study,a Logistic regression model on relationship between sardine Sardina pilchardus fishing ground and environmental variableswas established by stepwise regressionmethod based on fishing logbook,spatial information and oceanic environmental factors,including sea surface temperature(SST),chlorophyll-a concentration(Chl)and sea surface heightanomaly(SSHA)in western Africa coastal region from 2007 to 2011 in order to evaluate the optimal regressionmodel and each environmental variable impacting the fishing ground in different seasons.Results showed that therewasa close relationship between the occurrence of sardine population and geographical position.Itwas found that environmental factors played different roles in sardine distribution in different seasons:SST and SSHA showing significant affecting on the occurrence of the fish in spring,Chl and SSHA in summer,and SST in autumn and SSHA in winter.The findings provide definite referential value to analyze the formation mechanism of sardine fishing grounds.
Key words:Sardina pilchardus;West Africa coastal water;Logistic regression;fishing ground
中图分类号:S931.3
文献标志码:A
DOI:10.16535/j.cnki.dlhyxb.2016.02.017
文章编号:2095-1388(2016)02-0211-08
收稿日期:2015-05-22
基金项目:国家 “十二五”科技支撑计划项目 (2013BAD13B05,2013BAD13B01)