
图1 试验站位设置示意图
Fig.1 Schematic view of experimental set-up
注:W和E分别为试验设置的两个站位,W和E连线表示声传播的路径
Note:W and E represent the positions of two stations,the line between W and E indicates the sound transmission path
摘要:为了研究钱塘江涌潮的动力特征,于2013年11月5—6日在钱塘江杭州段采用沿海声层析 (Coastal acoustic tomography,CAT)和温盐深仪 (Conductivity temperature depth,CTD)进行了涌潮观测试验。两个观测站位分别设置在沿江两岸,站间距为3050 m,试验历时26 h,成功观测到两次涌潮的全过程。结果表明:两次涌潮到来前后,由双向传播时间差计算得到的断面平均流速的变化范围分别为0.39~-1.08、0.31~-0.85 m/s(东向流为正),水位升高的最大幅度分别为1.38、1.14 m;两次涌潮通过观测站位的波速分别为-8.69、-8.43 m/s;观测断面流量的变化范围为-7753.00~3504.49 m3/s,整个试验期间的平均流量为644.14 m3/s;涌潮的弗劳德数介于1.19~1.29之间,表明观测涌潮为波状涌潮;涌潮到达前后能量的损耗率小于0.6%,符合波状涌潮的能量守恒关系。
关键词:钱塘江;涌潮;沿海声层析;动力特性
钱塘江是浙江省第一大河,发源于安徽南部,流经皖、浙两省,最后经杭州湾注入东海,全长600多千米,流域面积约为55 558 km2。涌潮是入海口河口段的一种潮水暴涨现象[1]。当海水涨潮时,潮水涌入钱塘江漏斗状河口,潮水堆积会形成涌潮。每逢大潮期间,钱塘江都会形成雄伟壮观的涌潮。涌潮在传播过程中,由于河床地形和河道平面形态变化而呈现不同的形态潮景,最具代表性的有 “一线潮”、 “交叉潮” 和 “回头潮等[1]。 涌潮蕴藏着巨大的能量,同时也是一种自然灾害。它对河道、岸堤和涉水建筑冲击严重,不但影响航运交通和沿江两岸的开发,而且对两岸人民的生命和财产也构成潜在危胁。因此,研究涌潮对开发涌潮和防御潮灾都具有重要意义。
目前国内常用数值模拟的方法研究涌潮的宏观性质和微观性质。在涌潮宏观性质方面,苏铭德等[2-3]采用激波捕捉法初步模拟了钱塘江涌潮的形成和发展过程;李绍武等[4]建立了准三维涌潮数学模型,模拟河口区涌潮流场;潘存鸿等[5]应用基于KFVS格式的二维数值模型模拟了钱塘江涌潮形成、发展和衰减的全过程。在涌潮微观性质方面,曾剑等[6]用径向基函数 (RBF)建立模型预测了盐官站涌潮潮头的高度;杨火其等[7]通过水槽试验建立了涌潮流速与潮前水深、涌潮高度和涌潮传播速度的经验关系;潘存鸿等[5]结合实测数据分析了涌潮高度、流速、形态和压力等涌潮特性;谢东风等[8]建立了涌潮潮头坡度的解析式,复演了涌潮到达时刻潮头急剧增加的过程;林炳尧[1]综合分析了钱塘江涌潮的特性。在国外,Wolanskia等[9]基于实测数据分析了澳大利亚戴利河波状涌潮的动力特性;Bonneton等[10]首次在法国加伦河上观测了大振幅涌潮,研究了涌潮的流态和断面特征;Chanson[11]结合观测和数值模拟对涌潮进行了详细的综述。
由于涌潮能量巨大,并且钱塘江涌潮段水浅流急,使用常规仪器观测流速具有一定困难,故有关涌潮流速的资料相对匮乏[1]。目前,沿海声层析(Coastal acoustic tomography,CAT)为涌潮流速观测提供了新的方法,这是一种利用双向声传播方法观测流速的仪器,该仪器已经在中国舟山、台州三门湾、胶州湾、琼州海峡和钱塘江等地区成功完成了测流试验[12-16]。张传正等[15]首次利用CAT方法对钱塘江局部流速进行了观测,通过传播时间差计算的流速与多普勒流速剖面仪 (Acoustic doppler profiler,ADP)走航观测的结果基本一致,验证了CAT观测涌潮河段流速的可行性。随后,Zhu等[16]根据传播时间差与走航ADP观测流量建立了经验关系,得到了试验期间断面流量的时间序列,成功捕捉到了因钱塘江涌潮而引起的流量变化。本研究中,利用CAT和温盐深仪 (Conductivity temperature depth,CTD)对钱塘江杭州段涌潮进行了观测试验,对涌潮动力学特性进行了分析。
涌潮观测试验在距离杭州湾大约90 km的钱塘江杭州段进行。试验从2013年11月5日11:00开始到次日13:00结束,历时26 h。观测站位E站和W站的布置如图1所示,E站位于复兴大桥的桥墩上面,W站位于靠近钱塘江大桥附近的闸口水文站,两站相距3050 m,站位间的平均水深约为6 m。两站各设置一套CAT系统,仪器连接GPS和收发两用的换能器,换能器置于水中约3 m处。试验使用声信号为5 kHz的10阶M序列信号,发声间隔为15 s,换能器同时接收对方发射的声信号,数据自动储存在内部SD卡中。

图1 试验站位设置示意图
Fig.1 Schematic view of experimental set-up
注:W和E分别为试验设置的两个站位,W和E连线表示声传播的路径
Note:W and E represent the positions of two stations,the line between W and E indicates the sound transmission path
通过对数据的相关处理,可以获得对方站位发射的声信号到达的时间。假设沿着声传播路径的平均流速为Vm,声音在水中传播的平均速度为Cm,则从W站到E站的传播时间τ1和从E站到W站的传播时间τ2可以表示为[17]
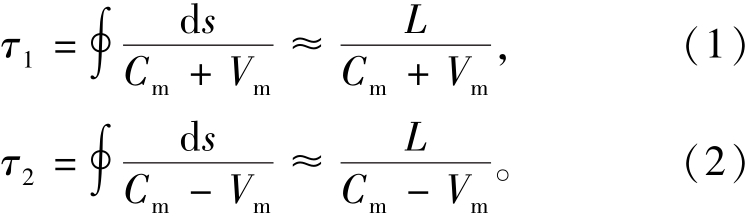
其中:L为站位之间的距离。将式 (1)和 (2)进行简单推导可得:
其中:¯τ=(τ1+τ2)/2, Δτ=τ2-τ1。 假设 ¯τ≈τ1≈τ2,对式 (3)和式 (4)进行微分和变换,得到Vm的相对误差为
由于GPS时钟精确同步,¯τ≫δτ,则Δτ≫δ(Δ¯τ), 故式 (5)中第二项和第三项可以忽略,式 (5)可简化为
在本次试验中,两站位间距L=3 km,GPS误差为10 m,流速相对误差δVm/Vm=0.003 3,即当平均流速为Vm=1 m/s时,对应的误差值为0.003 3 m/s。这样,在保证高精度传播时间的观测条件下,由距离误差导致平均流速的观测误差极小。
由于两个站位离岸距离相对于整个江面的宽度(1200 m)都较小且站位靠近岸边的水深较浅,本研究中假定观测站位距岸边的流量忽略不计。根据张传正[18]提出的观测区域双向声信号传播时间差Δτ与流量Q的经验关系式对断面流量进行推算:
为了观测涌潮期间水位、温度和盐度的变化,本研究中在两个观测站位处各放置了一台锚系CTD(RBR,XR-420)。CTD距河床高度为0.35 m,采样间隔为2 s。
如图2所示,涌潮沿钱塘江自下游向上游传播,通常把潮波传播的速度称为波速。这里将涌潮波速和涌潮高度的计算近似地视为一维问题。涌潮波速可用下面的理论公式[9]进行估算:
其中:h1和h2分别为涌潮到来前后的水深 (m); g为重力加速度 (m/s2)。根据波速的定义,实际观测波速的表达式如下:
其中:R为涌潮从E站到W站的传播距离;t1和t2分别为涌潮到达E站和W站的时间。
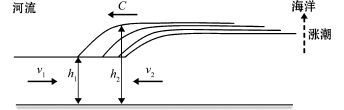
图2 涌潮示意图
Fig.2 Sketch of the tidal bores
涌潮高度是衡量涌潮大小的重要参数之一。用Δη=h2-h1表示涌潮前后高度,Δv=v2-v1表示断面平均流速差,则涌潮前后流速差与涌潮高度的理论关系为[17]
其中,Δv可通过传播时间差计算得到,涌潮前后的水深可通过CTD观测得到。假设涌潮前后能量守恒,则可以通过涌潮前后的流速差来推测当时理论上的涌潮高度。
2.1 声信号
图3为W站和E站接收到信号信噪比 (Signal to noise ratio,SNR)的时间序列。试验观测显示, SNR在2.056~2.066 s之间有明显的峰值,SNR的峰值介于100~300之间,SNR最大峰值对应的时间认为是声信号到达的时间。从图3可知,声信号实际到达时间与预期到达时间基本一致 (3050/ 1480=2.06 s,3050 m为两站距离,1480 m/s为根据现场观测的温度、盐度和深度计算所得到的声波在水中的传播速度)。由于试验期间W站在11月5日16:00至17:30之间GPS天线发生故障,故出现少量数据缺失。
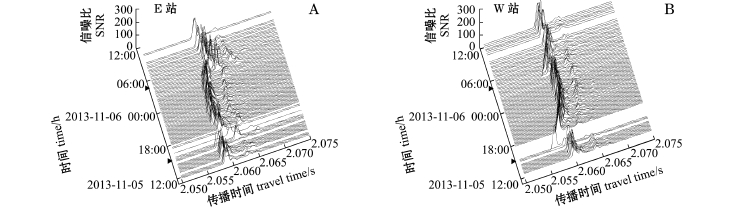
图3 信噪比时间序列
Fig.3 Tim e series of signal-to-noise ratio
注:黑色三角表示涌潮到来的时间
Note:The black triangles represent the timeswhen the tidal bores arrive
2.2 水深、盐度、温度、声传播时间、流速和流量的观测
图4-A为试验期间在E站和W站用CTD观测得到的水深时间序列。第一次涌潮到来时,E站和W站水位升高的最大幅度分别为1.31、1.38 m;第二次涌潮到来时,E站和W站水位升高的最大幅度分别为0.94、1.14 m。根据涌潮到来前后的水深,由式 (8)计算得到两次涌潮到来时E站和W站的理论波速的平均值分别为8.62、8.54 m/s。另外,根据站位水深的变化可确定涌潮到达的时刻,由式 (9)可得到实际波速分别为8.69、8.43 m/s。理论波速与实际波速基本一致。
图4-B为在E站和W站用CTD观测得到的盐度时间序列。第一次涌潮开始约2 h,E站盐度由0.4逐渐增大至1.34,W站盐度由0.4逐渐增大至0.71。表明第一次涌潮期间,有海水从下游入侵到上游。第二次涌潮过后,观测区域的盐度没有出现明显的变化。
图4-C为在E站和W站用CTD观测得到的水温时间序列。在整个试验观测期间,水温变化不大,其变化范围为19.4~20.2℃。涌潮过后,水温整体有降低的趋势。
图4-D为根据CAT观测得到的双向声信号平均传播时间的时间序列。整个试验期间,双向声信号的平均传播时间为2.058~2.062 s。两次涌潮到来前后,双向声信号平均传播时间均发生较大变化,与之相对应的是声速减小。如果传播时间的增大是由温度变化引起,则温度变化必须降低大约0.52℃,而从图中可以看出,涌潮过后水温变化不大,而且仅第一次涌潮过后温度稍微升高,因此,双向声信号的平均传播时间增大的主要原因不是温度的变化,而是涌潮的到来让换能器的相对位置发生了一定变化。
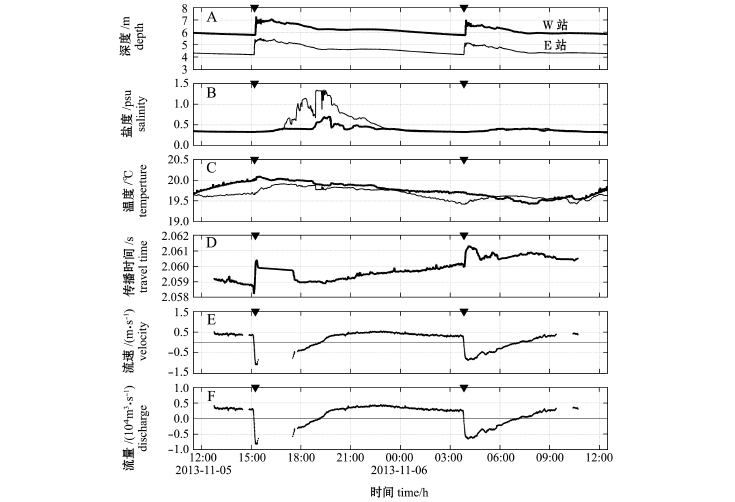
图4 水深、盐度、温度、双向声信号平均传播时间和计算得到的流速和流量时间序列
Fig.4 Time series of water depth,salinity,tem perature,mean reciprocal travel time,velocity and calculated discharge
注:图A、B、C中细实线和粗实线分别表示E站和W站观测值;两个黑色的三角形为涌潮到来的时间
Note:The thin solid line represents the values of E station and the thick solid line indicates the values of W station in Figures A,B,and C;the black triangles represent the arrival time of tidal bores
根据式 (3)和双向声信号传播时间差求得断面平均流速的时间序列如图4-E所示。两次涌潮到来之前,流速基本稳定在0.39、0.31 m/s。涌潮到来之后,涌潮流 (西向流)与上游淡水流(东向流)的流速相互抵消,流向发生逆转,流速在20 min内达到最大。两次涌潮中观测到的最大流速分别为-1.08、-0.85 m/s。流向逆转为西向流之后大约1.5 h,涨潮流转变成落潮流,流速逐渐减小,直到流向转向东向流之后流速缓慢增大,并逐渐趋于平稳。从涌潮开始到结束的整个作用过程大约持续了5 h 40 min。
根据式 (7)和双向传播时间差求得断面流量的时间序列如图4-F所示。试验观测期间,最大东向流 (最大落潮流量)出现在无涌潮影响期间,最大西向流 (最大涨潮流量)出现在第一次涌潮到来之后。对缺失数据进行插值,得到观测期间最大东向流量和西向流量分别为3504.49、-7753.00 m3/s,平均流量为644.14 m3/s。两次涌潮带来的西向输运量分别为9.09×107、6.83×107m3,相当于5~6个西湖的总蓄水量 (1.43×107m3)[19]。
为了判别涌潮的类型,本研究中引入了弗劳德数 (Froude number,Fr),其为水跃强度的动力参数,可用潮流速与波速间的关系表示[9]:
当Fr<1时,潮波推进的波列未形成涌潮;当1≤Fr<1.7时,涌潮为波状涌潮;当Fr≥1.7时,流态发生根本变化,不再具有波动性,变成破碎涌潮。根据观测数据求得两次涌潮的 Fr=1.19~1.29,表明观测期间的涌潮类型属于波状涌潮。
当波速和流速相等时的水流为临界流,临界流对应的水深即为临界水深,临界水流对应的Fr为1,临界水深 (dc)可由潮流速(v1)、水深(h1)和波速(C)表示[11]:
当实际水深大于临界水深时,对应的水流为亚临界流,流速小于临界流速,则Fr<1;当实际水深小于临界水深时,对应的水流为超临界流,流速大于临界流速,则Fr>1。在观测的流场中,计算得出两次涌潮中E站临界水深分别为4.98、4.80 m, W站临界水深分别为6.63、6.48 m,E站和W站的临界水深均介于涌潮前后观测的水深之间,说明涌潮导致流向逆转,本次观测到的两次涌潮流场中均存在亚临界流和超临界流转换的流动。
涌潮的种类不同,其能量的耗散也不同。根据涌潮前后的水深关系,可得出涌潮前后单位水体的能量差,且涌潮的能量耗散为[20]
式 (13)表明,涌潮的能量耗散与Fr有关。假如涌潮发生前后的能量耗散忽略不计,可认为能量近似守恒。根据能量和动量守恒得到如下关系[11]:
其中:M为动量;E为单位质量的能量 (比能)。
图5-A为根据式 (13)计算得到的能量耗散和Fr的关系。当 Fr<1.2时,能量耗散率小于0.22%;当Fr=1.2~2.0时,能量损耗率会增加到9.08%,增幅较快;当Fr>2.0时,能量损耗增加趋势变缓。对钱塘江涌潮的观测表明,涌潮能量损失小于0.6%,可以忽略不计,涌潮到来前后的能量基本守恒。图5-B为根据式 (14)、(15)计算得到本次观测涌潮能量与动量的关系图,可以看出,试验所观测的数据完全处于参数化的M-E曲线上,表明观测数据满足能量近似守恒关系。
图6为根据式 (10)计算得到的涌潮前后流速差与涌潮高度的关系,可以看出,流速差越大对应的潮头高度就越高,试验观测值与理论值基本吻合。
2013年11月5—6日在钱塘江杭州段进行了一次涌潮观测试验,成功地观测到两次涌潮期间水位、流速的变化,得到主要结论如下:
(1)两次涌潮发生时,涌潮前后观测断面流速的变化范围分别为 0.39~-1.08 m/s和0.31~-0.85 m/s(东向流为正),水位升高的最大幅度分别为1.38、1.14 m,两次涌潮通过观测站位的波速分别为-8.69、-8.43 m/s。
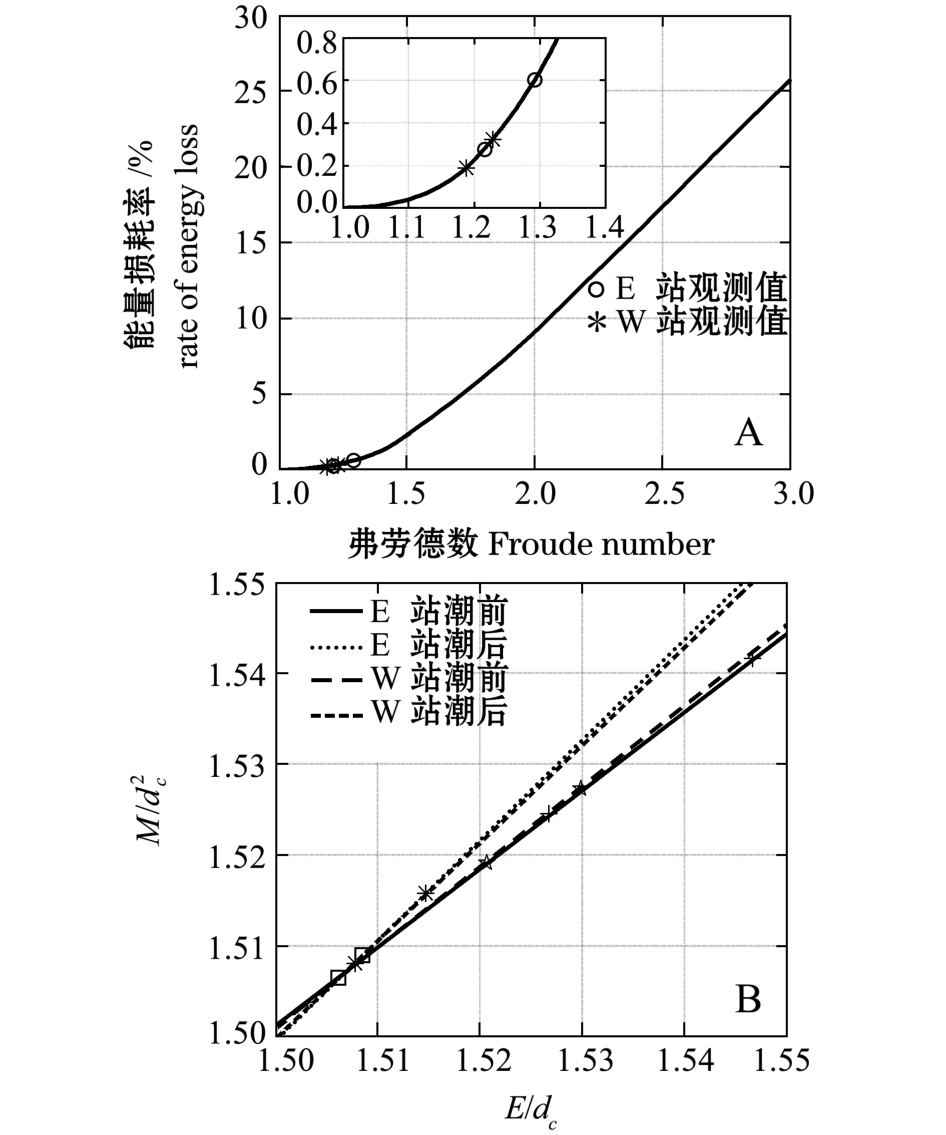
图5 涌潮能量耗散率与弗劳德数及涌潮能量与动量的关系
Fig.5 General relationship between energy dissipation rates and Froude num ber,and the relationship between energy and momentum of the tidal bores
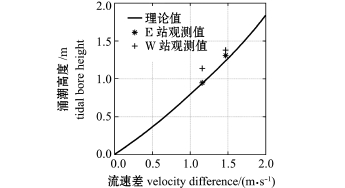
图6 流速差与涌潮高度关系
Fig.6 Relationship between velocity difference and wave height
(2)观测期间,最大东向流 (最大落潮流量)出现在无涌潮影响期间,最大西向流 (最大涨潮流量)出现在涌潮导致江水逆流阶段,最大东向流和西向流流量分别为3504.49、-7753.00 m3/s,平均流量为644.14 m3/s。两次涌潮带来的西向输运量分别为9.09×107、6.83×107m3。
(3)涌潮的弗劳德数为1.19~1.29,表明观测的涌潮是波状涌潮。临界水深均介于涌潮前后的水深之间,涌潮流场中存在亚临界流和超临界流转换的流动。
(4)涌潮到达前后能量的损耗率小于0.6%,表明波状涌潮的能量损耗可基本忽略不计,观测数据都处于参数化的M-E曲线上,涌潮的能量基本保持守恒。
参考文献:
[1] 林炳尧.钱塘江涌潮特性[M].北京:海洋出版社,2008:1-52.
[2] 苏铭德,徐听,朱锦林,等.数值模拟在钱塘江涌潮分析中的应用:Ⅰ.数值计算方法[J].力学学报,1999,31(5):521-533.
[3] 苏铭德,徐听,朱锦林,等.数值模拟在钱塘江涌潮分析中的应用:Ⅱ.计算结果和分析[J].力学学报,1999,31(6):700-716.
[4] 李绍武,卢丽锋,时钟.河口准三维涌潮数学模型研究[J].水动力学研究与进展A辑,2004,19(4):407-415.
[5] 潘存鸿,鲁海燕,曾剑.钱塘江涌潮特性及其数值模拟[J].水利水运工程学报,2008,6(2):1-9.
[6] 曾剑,孙志林,熊绍隆,等.基于径向基函数网络的钱塘江涌潮模型及其应用[J].浙江大学学报:工学版,2007,41(9):1457-1461.
[7] 杨火其,潘存鸿,周建炯,等.涌潮水动力学特性试验研究[J].水电能源科学,2008,26(4):136-138.
[8] 谢东风,潘存鸿,陆波,等.基于实测数据的钱塘江水动力学特性研究[J].水动力学研究与进展A辑,2012,27(5):501-508.
[9] Wolanski E,Williams D,Spagnol S,et al.Undular tidal bore dynamics in the Daly Estuary,Northern Australia[J].Estuarine, Coastal and Shelf Science,2004,60(4):629-636.
[10] Bonneton P,Van de Loock J,Parisot JP,et al.On the occurrence of tidal bores-the Garonne River case[J].Journal of Coastal Research,2011,SI64:1462-1466.
[11] Chanson H.Tidal bores,Aegir,Eagre,Mascaret,Pororoca:Theory and Observations[M].Singapore:World Scientific Publishing Company,2012:9-20
[12] Zhu X H,Kaneko A,Wu Q,etal.Mapping tidal current structures in Zhitouyang Bay,China,using coastal acoustic tomography[J]. IEEE Journal of Oceanic Engineering,2013,38(2):285-296.
[13] 朱泽南,朱小华,张传正,等.三门湾沿海声层析潮流观测实验[J].地球物理学报,2015,58(4):1-12.
[14] Zhu X H,Zhu Z,Guo X,et al.Measurement of tidal and residual currents and volume transport through the Qiongzhou Strait using coastal acoustic tomography[J].Continental Shelf Research, 2015,108:65-75.
[15] 张传正,朱小华,吴清松.钱塘江双向声传播测流实验研究[J].地球物理学报,2010,53(7):1741-1748.
[16] Zhu X H,Zhang C,Wu Q,et al.Measuring discharge in a river with tidal bores by use of the coastal acoustic tomography system [J].Estuarine,Coastal and Shelf Science,2012,104/105:54-55.
[17] Munk W,Worcester P,Wunsch C.Ocean Acoustic Tomography [M].New York:Cambridge University Press,1995.
[18] 张传正.沿海声层析技术在我国近海的应用研究[D].杭州:国家海洋局第二海洋研究所,2011.
[19] 杭州市地方志编纂委员会.杭州年鉴[M].北京:方志出版社,2004.
[20] 张玮,徐金环,李国臣,等.涌潮分析与波速计算[J].水利水运科学研究,1999,6(2):158-164.
Observation and dynam ic characteristics of tidal bore in Qiantang River,China
Abstract:A 26-hour observation of tidal boreswas carried out by a coastal acoustic tomography(CAT)system and conductivity temperature depth(CTD)in two stations at both sides with a distance of 3050 m diagonally across Qiantang River from 5 to 6 November,2013 to valuate the dynamic characteristics of tidal bore in Qiantang River, China.The range-averaged current velocities calculated from the reciprocal sound transmission data were changed from 0.39 m/s to-1.08 m/s before arrival of tidal bore with themaximalwater level changes of 1.38 m and from 0.31 m/s to-0.85 m/s after arrival of tidal borewith themaximalwater level changes of1.14 m(the positive velocity towards the east).Themean phase speeds of two tidal bores were estimated to be-8.69 m/s and-8.43 m/s at the two stations,respectively.During the whole experiment,the volume transport was varied from -7753.00 m3/s to 3504.49 m3/s through the section,with amean of644.14 m3/s.The Froude numbers of tidal bores were estimated to be from 1.19 to 1.29,indicating that the observed tidal boreswere undular bore,with tidal bore energy losses of less than 0.6%,conforming to energy conservation relations for undular bores.
Key words:Qiantang River;tidal bore;coastal acoustic tomography system;dynamic characteristics
中图分类号:P731.23
文献标志码:A
收稿日期:2015-01-12
基金项目:国家自然科学基金资助项目 (41276095,41476020,41321004,41176021,41576001);国家海洋局第二海洋研究所基本科研业务费专项 (JT1402);卫星海洋环境动力学国家重点实验室自主项目 (SOEDZZ1403,SOEDZZ1501);国家海洋局第二海洋研究所SOED开放课题基金资助项目 (SOED1511);辽宁省教育厅科研项目 (L2012268)
DOI:10.16535/j.cnki.dlhyxb.2015.05.022
文章编号:2095-1388(2015)05-0567-06