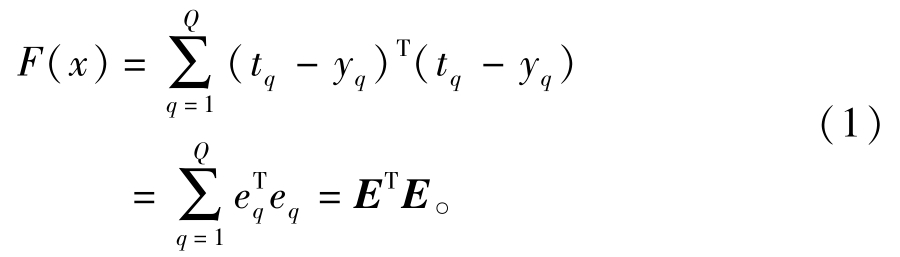
缪新颖1,葛廷友2,高辉3,王建彬1
(1.大连海洋大学信息工程学院,辽宁大连116023;2.大连海洋大学职业技术学院,辽宁大连116300; 3.大连海洋大学理学院,辽宁大连116023)
摘要:水产养殖池塘是一个多变量、非线性和大时延系统,其中溶解氧的预测也是一个复杂的问题。针对大连某水产养殖池塘,作者建立了一个基于Levenberg–Marquardt(LM)神经网络和遗传算法(GA)的溶解氧预测模型GA-LM,并将该模型与传统的BP神经网络进行比较分析。结果表明:使用本研究中建立的GA-LM模型预测的溶解氧值和实际测定值吻合较好,预测更为精准,运行时间明显减少。
关键词:溶解氧;Levenberg–marquardt算法;遗传算法;预测模型
水质测定是一个包括多种物理、化学和生物参数的复杂过程[1]。其中,池塘溶解氧作为养殖水域必控的水环境因子越来越受到重视。因此,及时掌握池塘水域溶解氧的动态变化规律,在缺氧之前进行池塘溶解氧的事前预测是水产养殖生产中迫切需要解决的问题。
池塘溶解氧预测是一个非线性的复杂过程,利用统计的方法很难保证预测精度[2]。而神经网络(Neural network,NN)因为其无需输入变量与输出变量间复杂的相关假设,成为模拟和解决非线性问题的理想工具之一,并开始应用于溶解氧预测[3-6]。但是,采用传统的BP神经网络常常导致训练时间较长且易陷入局部极小点。Levenberg-Marquardt(LM)算法利用高斯-牛顿法可以在最优值附近产生一个理想的搜索方向,从而保持较快下降速度的特点,使网络能够有效收敛,大大提高了网络的收敛速度和泛化能力。
遗传算法(Genetic algorithm,GA)是一种模拟自然进化过程搜索最优解的方法。它借鉴了生物界自然选择和自然遗传机制,即基于达尔文适者生存、优胜劣汰的进化原则,对包含可行解的群体反复使用遗传学的基本操作,不断生成新的群体,使种群不断进化。同时,以全局并行搜索技术来搜索优化群体的最优个体,以求得满足要求的最优解。GA算法的最大优点是,即使对多态的或非连续的函数,它也能获得全局最优解,适合用来优化神经网络的结构。基于以上考虑,本研究中,作者建立了一个综合GA和LM两种算法优点的GA-LM模型,并将其与传统的BP算法进行比较分析。
1.1 影响池塘溶解氧的因素分析
影响池塘溶解氧的因素十分复杂,主要包括水呼吸、养殖生物的呼吸、底泥以及池塘水体温度、水体含氮量和空气中氧气组分的分压力等[7-9]。
本试验中,取样池塘设在大连市瓦房店地区谢屯,位于渤海东部区的普兰店湾沿岸,养殖池塘总面积约6.67 hm2。综合考虑各变量的可测性,选取温度、亚硝酸盐、氨氮和总氮4个变量作为输入变量,输出变量为池塘溶解氧。温度、亚硝酸盐氮、总氨氮和溶解氧使用美国YSI600XLM多参数水质监测仪现场测定,总氮值使用美国HACH公司制造的IL500全自动总氮分析仪测定。
对于这样一个4输入、1输出的非线性系统,非常适合利用神经网络进行预测。从2006—2009三年所搜集的监测数据中选取其中的100组数据作为建模数据,其中80组作为训练样本,20组作为测试样本,对网络模型进行校验。
1.2 GA-LM预测模型的算法
神经网络的传统学习算法,如BP(Back-Propagation)通常采用梯度下降法,计算量较大,容易陷入局部极小点,且学习效率很低。为此,本研究中选用LM算法以弥补BP算法的不足。LM算法是利用高斯-牛顿法可以在最优值附近产生一个理想的搜索方向,从而保持较快下降速度的特点,在最速梯度下降法和高斯-牛顿法之间自适应调整网络权值,使每次迭代不再沿着单一的负梯度方向,而是允许误差沿着恶化的方向进行搜索,使网络能够有效收敛,大大提高了网络的收敛速度和泛化能力。由BP算法改进得到LM算法的具体过程如下:
假设BP神经网络有Q对训练样本(pq,yq), q=1,2,…,Q,其中:pq代表第q对训练样本中的输入信号;yq代表第q对训练样本对应的实际网络输出信号;令tq代表第q对训练样本中的教师信号,则对应的误差eq=tq-yq。BP算法的训练目的是希望训练样本的教师信号与网络的输出信号之间的误差平方和最小,这个误差平方和函数就是要优化的目标函数F:
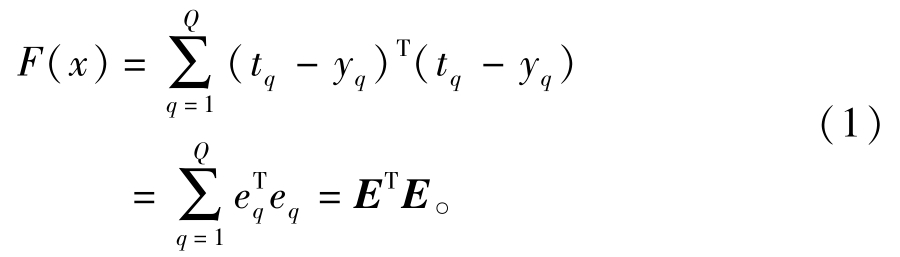
误差对权值w微分的雅可比矩阵为J(w),则LM算法权值的调整算法为
其中:I是单位矩阵;μ是LM算法内部使用的一个大于零的调整因子,用于控制LM算法的迭代。当其接近零时,LM算法接近高斯-牛顿法;当其很大时,LM算法近似于传统BP的最速下降法。通过自适应调整该值,LM算法可以完成梯度下降法与高斯-牛顿法的较好结合。在实际操作中,该值是一个试探性的参数,算法开始时μ取小值,如果求得的Δw能使误差指标函数F(x)降低,则该值降低到μ/β(其中β>1);反之,该值增加至β·μ。本研究中μ初始值设为0.01,β取为5。
1.3 GA-LM预测模型的结构
1989年Robert Hecht-Nielson证明了对于任何在闭区间内的一个连续函数都可以用一个隐层的BP网络来逼近[10],因而一个三层的BP网络可以完成任意的m维到n维的映射。故在本研究中,将隐层的数目确定为1。
隐层节点数的选择是一个十分复杂的问题,很多文献均采用了试凑法[11]。很明显,试凑法简单,但缺乏科学理论依据,并且运行费时。本研究中采用GA算法这个有效的搜索方法来确定神经网络的最优结构,即所采用的3层LM神经网络的隐层节点数和最优权值及阈值均由GA来完成。整个过程主要包括以下3个阶段:
1)编码。为了清晰表示神经网络结构,将一条染色体分为结构基因和权重基因。结构基因采用二进制编码形式,放在前面,表示隐层节点是否存在。其中“1”表示隐层节点存在,“0”表示隐层节点不存在;权重基因采用实数编码,放在后面,表示连接权值和阈值。如图1所示,假设神经网络有m个输入节点,n个输出节点,最多有L个隐层节点(结构基因共L位),则相应的连接权值和阈值为L×(m+n)个,即权重基因共L×(m+n)位,与第i个隐层节点有关的权值和阈值编码被放在从L +(i-1)×(m+n)+1到L+i×(m+n)的位置上。
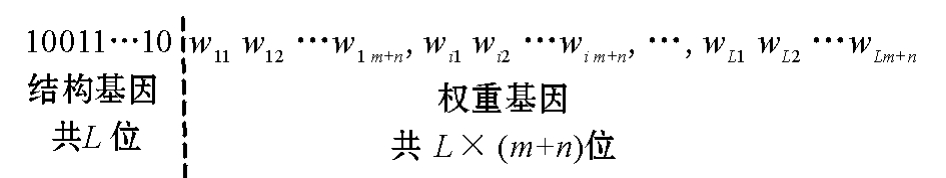
图1 染色体结构示意图
Fig.1 Structure of chromosomes
2)适应度评价。计算每一个个体的评价函数,用于评估该个体的适应度。本研究中所采用的适应度函数为
其中:V是经神经网络训练得到的溶解氧值;T是实际测定的溶解氧值;E是误差平方和;F是适应度函数。通过向适应度高的进化过程,使得算法向误差减小以及网络结构简单的方向进行。
3)遗传算子[12]。本研究中选择算法采用最常用的轮盘赌策略。因为二进制编码和实数编码同时存在,所以交叉和变异算子均采用了混合策略。其中单点交叉应用于结构基因,算术交叉用于权重基因;同样,在变异时,依然要判断编码的类型,二进制编码的结构基因采用基本位变异算子,实数编码的权重基因采用非均匀变异算子。
另外,本研究中有两个终止判别条件。当迭代次数达到预设的最大进化代数时,或当训练目标均方差(MSE)小于ε=0.001时,算法终止。
1.4 GA-LM预测模型的应用
本研究中采用Matlab进行编程构成GA训练
LM神经网络,其算法步骤如下:
1)对输入数据进行归一化处理。网络学习之前,为了提高精度,将试验数据规范化,即将实测数据通过premnmx函数转换为[-1,1]的值。
2)对运行参数进行设置。取种群大小N= 100,初始隐层节点数(最大隐层节点数)L=22,进化最大代数为100,交叉率为0.6,变异率为0.08。训练算法采用trainlm;隐层和输出层的激活函数分别采用连续可微的tansig和线性的purelin。
3)初始化种群。结构基因采用二进制编码;权重基因采用实数编码。
4)对每个染色体解码并计算适应度。结构基因为1时,与其对应的权重基因有效;结构基因为0时,与其对应的权重基因无效。结构基因为1的个数即为隐层节点数,与其对应的权重基因即为LM神经网络的权值和阈值,用其构造神经网络,计算每个染色体的适应度。
5)按其适应度采用轮盘赌策略选择和复制个体,并按照“1.3”节中的方法进行遗传算子相应的操作生成新的种群。
6)判断是否满足最大进化代数或MSE小于0.001的停止准则,若满足则转到步骤7);若不满足则返回步骤4)。
7)对每个染色体解码,构造LM神经网络,评价网络性能。
8)利用训练好的LM网络进行预测并利用postmnmx函数对预测结果进行反归一化。
经过迭代计算,隐层有12个节点,即利用GA得到的最优网络结构为4-12-1三层神经网络,图2为最优网络结构示意图。
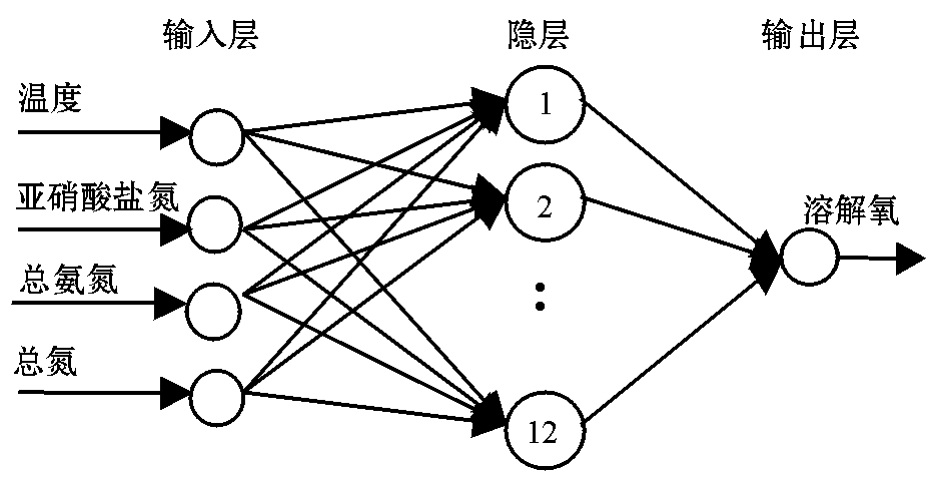
图2 最优神经网络的结构图
Fig.2 The optimal structure of a neural network
将利用本研究中所提出的GA-LM模型预测的结果与传统BP神经网络进行比较。传统BP神经网络的隐层节点数采用常见的经验法+试凑法确定。
其中:m和n分别为神经网络的输入和输出节点数;α为一个0~10的常数。
将m=4,n=1代入,可得P的值为2~13,在此基础上以均方差MSE为评判标准,利用试凑法确定BP网络的隐层节点数,结果见图3。可以看出,当隐层节点数为10的时候,MSE最小,故BP神经网络的网络结构为4-10-1。
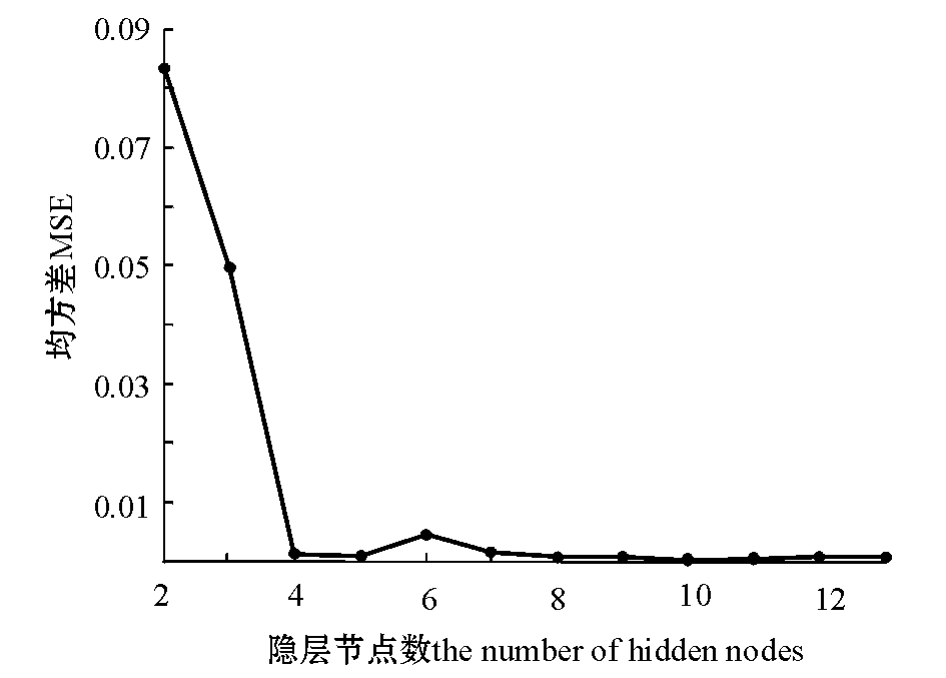
图3 用试凑法确定隐层节点数
Fig.3 Determination of the number of hidden nodes by trial and error approach
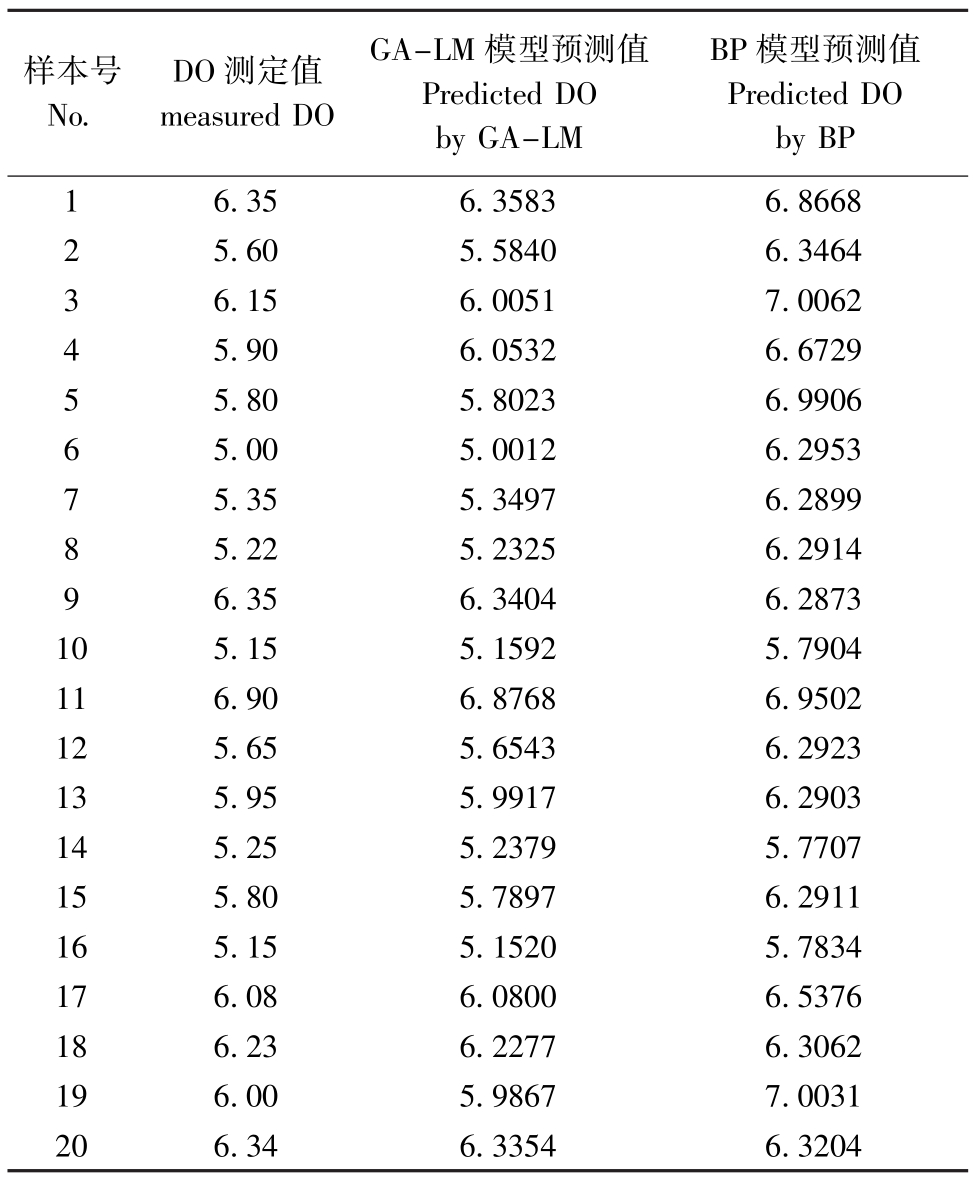
利用传统BP神经网络与本研究中建立的GALM模型对20组测试样本进行预测,溶解氧的实际测定值及模型预测值如表1所示。可以看出,采用GA-LM预测的溶解氧值与测定值吻合程度远远高于BP算法。
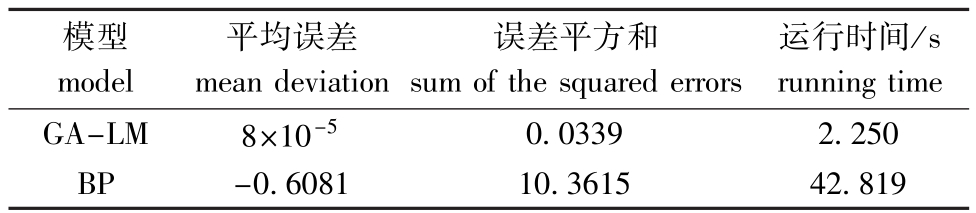
对两个模型的性能参数进行比较(表2),可以看出:GA-LM模型的两个统计参数平均误差和误差平方和远远小于BP网络,说明GA-LM模型预测精度明显提高;从预测的运行时间上看,采用试凑法的传统BP神经网络明显比GA-LM模型预测时间长很多。这说明采用遗传算法优化神经网络结构,与试凑法相比,大大节省了运行时间。
面对养殖池塘这样一个复杂的非线性系统,作者在传统BP神经网络基础上,从算法和结构上进行了很大的改进。结果表明:本研究中建立的GA -LM溶解氧预测模型,既发挥了LM神经网络预测精度高、泛化能力强的特点,同时又能体现出GA的优势,快速优化网络结构,节省运行时间,进一步提高预测性能。
表1 溶解氧的测定值及模型预测值
Tab.1 The measured and predicted values of dissolved oxygen(DO)levelsmg/L
样本号No. DO测定值measured DO GA-LM模型预测值Predicted DO by GA-LM BP模型预测值Predicted DO by BP 16.356.35836.8668 25.605.58406.3464 36.156.00517.0062 45.906.05326.6729 55.805.80236.9906 65.005.00126.2953 75.355.34976.2899 85.225.23256.2914 96.356.34046.2873 105.155.15925.7904 116.906.87686.9502 125.655.65436.2923 135.955.99176.2903 145.255.23795.7707 155.805.78976.2911 165.155.15205.7834 176.086.08006.5376 186.236.22776.3062 196.005.98677.0031 206.346.33546.3204
表2 两个模型性能的比较
Tab.2 Performance comparison of two prediction models
模型model running time GA-LM8×10-5平均误差mean deviation误差平方和sum of the squared errors运行时间/s 0.03392.250 BP-0.608110.361542.819
参考文献:
[1] Rankovic'a V,Radulovic'a J,Radojevic'b I,et al.Neural network modeling of dissolved oxygen in the Gruža reservoir,Serbia[J]. Ecological Modelling,2010,221(4):1239-1244.
[2] Boano F,Revell R,Ridolfi L.Stochastic modelling of DO and BOD components in a stream with random inputs[J].Advances in Water Resources,2006,29(9):1341-1350.
[3] Schmid B H,Asce M,Koskiaho J.Artificial neural network modeling of dissolved oxygen in a wetland pond:the case of Hovi,Finland[J].Journal of Hydrologic Engineering,2006,11(4):188-192.
[4] Faruk D Ö.A hybrid neural network and ARIMA model for water quality time series prediction[J].Engineering Applications of Artificial Intelligence,2010,23(2):586-594.
[5] Zhang S,Song W T,Mo J Y,et al.A neural network prediction model for dissolved oxygen in nutrient solution with MATLAB[J]. Environmental Informatics Archives,2005(3):207-210.
[6] Chen D J,Lu J,Shen Y N.Artificial neural network modelling of concentrations of nitrogen,phosphorus and dissolved oxygen in a non-point source polluted river in Zhejiang Province,southeast China[J].Hydrological Processes,2009,24(10):290-299.
[7] 高艳萍,于红,崔新忠.基于优化BP网络的工厂化水产养殖水质预测模型的实现[J].大连水产学院学报,2008,23(3):221-224.
[8] Deng C H,Wei X J,Guo L X.Application of Neural Network Based on PSO Algorithm in Prediction Model for Dissolved Oxygen in Fishpond[C]//Proc.6th World Congress on Intelligent Control and Automation(WCICA 2006).New york:IEEE Press,2006: 9401-9405.
[9] 郭连喜,邓长辉.基于模糊神经网络的池塘溶解氧预测模型[J].水产学报,2006,30(2):225-229.
[10] 张立明.人工神经网络的模型及其应用[M].上海:复旦大学出版社,1993.
[11] 王红英,樊增绪,薛松堂.一种新的池塘溶解氧预测模型[J].农业工程学报,1997(4):145-147.
[12] 周明,孙树栋.遗传算法原理及其应用[M].北京:国防工业出版社,2000.
A prediction model for dissolved oxygen level in a fish pond based on combination of neural network and genetic algorithm
MIAO Xin-ying1,GE Ting-you2,GAO Hui3,WANG Jian-bin1
(1.School of Information Engineering,Dalian Ocean University,Dalian 116023,China;2.Vocational and Technical College,Dalian Ocean University,Dalian 116300,China;3.School of Science,Dalian Ocean University,Dalian 116023,China)
Abstract:The prediction of dissolved oxygen(DO)level is complicated in aquaculture ponds as a complex system with multi-variables,nonlinearity and long-time lag.In this study,GA-LM,a hybrid neural network model combining Levenberg Marquardt(LM)algorithm and Genetic Algorithm(GA)was developed for DO level predicting in an aquaculture pond at Dalian,China.The The comparison of performance of GA-LM with the conventional Back -Propagation(BP)algorithm revealed that the predicted DO values using GA-LM model are in good agreement with the measured data,indicating that the model is capable of predicting DO accurately and rapidly.
Key words:dissolved oxygen;levenberg-marquardt algorithm;genetic algorithm;prediction model
文章编号:2095-1388(2011)03-0264-04
中图分类号:S931.3
文献标志码:A
收稿日期:2010-08-12
基金项目:国家自然科学基金资助项目(61004063);辽宁省教育厅高等学校科研计划项目(L2010073);辽宁省海洋与渔业厅项目(201006);辽宁省科学技术计划项目(2010216008)
作者简介:缪新颖(1977-),女,讲师。E-mail:miaoxinying@dlou.edu.cn