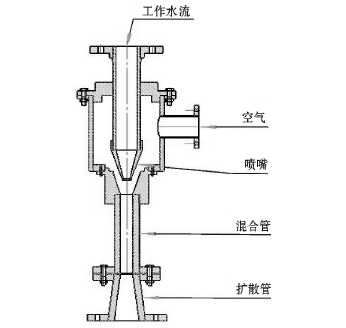
图1 射流器的结构
Fig.1 Schematic diagram of the ejector
贾惠文1、2,曹广斌1,蒋树义1,韩世成1,陈中祥1
(1中国水产科学院黑龙江水产研究所,黑龙江哈尔滨150070;2上海海洋大学工程学院,上海201306)
摘要:利用κ-ε双方程湍流模型对自行设计的射流式增氧机内部流场进行了模拟,得到了流场内部各个参数的分布图,揭示了混合管内部的流动状态,为射流式增氧机的参数优化和性能预测提供了可靠的手段。通过对射流器仿真数据的分析,得出混合管与喷嘴截面积比的最佳值为2.33,并通过增氧试验验证,证明仿真结果与试验结果相吻合。
关键词:射流增氧机;数值模拟;面积比
射流增氧是水产养殖中常用的技术手段,它的优点是兼有推流和增氧的双重作用[1],并能够对最缺氧的池底水体进行直接增氧,对提高养殖池底层水体的溶解氧有较好的效果[2]。相对于其它安置于水面的增氧机,射流式增氧机可以在水体的不同深度工作,也可以对冰封的水体增氧,它已被广泛应用于池塘养殖和工厂化循环水养殖系统中。
射流式增氧机的核心部件是射流器,它是一种两相或多相混合设备。国外学者很早就对射流器的工作原理进行理论分析,1942年Keenan和Neumann建立了一维的能量、质量和动量守恒方程来预测射流器的性能[3];Sherif建立了两相流模型,通过引入含气率来考虑两相的相互作用[4];Bartosiewicz等分别采用几种不同的湍流方程来分析空气在射流器内的流动情况[5]。为了提高射流器的性能,近年来研究人员对射流器进行了深入的研究[6-7],但由于射流器混合管内的流动状态较为复杂,目前的生产设计中不得不采用经验公式[8]。为优选射流器的设计尺寸并找出各尺寸对性能的影响,国内学者做了大量的射流器增氧机充氧试验,该试验对试验场地和试验设备有严格要求[9],其研究的时间长、投资高,试验结果受环境因素影响较大。随着计算机技术和计算流体动力学(CFD)的发展,越来越多的研究人员开始应用CFD方法模拟流体在设备中的流动状态。对流体的数值模拟不仅可以向设计者提供大量信息,而且费用低、研制周期短,同时还可直观地观察设备中流体的工作情况,为设计流体机械提供了便利。
Fluent软件是近年来得到广泛应用的商用CFD软件,它的功能强,适应面广,能够计算流体流动和热传导模型、辐射模型、相变模型及多相流模型等,针对每一种物理问题的流动特点,用户可以选择适合的数值解法、差分格式等,以求在计算速度、稳定性和精度方面达到用户的要求。Fluent软件可以与不同领域的软件联系起来,导入Auto CAD或者Pro/E等绘图软件的图形,并采用统一的前后处理工具,使科研工作者能够从繁复的编程等劳动中解放出来,集中精力关注物理问题本身的探索。基于这些特点,Fluent软件已被广泛应用于流体机械的数值模拟中[10-12]。
本研究中,作者在设计工厂化水产养殖射流增氧设备的过程中,利用流体力学仿真软件Fluent对射流器内部流场进行了数值模拟,通过比较不同设计尺寸射流器的仿真结果,来确定射流器增氧效果最好的设计尺寸;并对所模拟的几组射流器进行水体增氧效果试验,对仿真模拟设计尺寸进行检验,
结果证明所建模型能够准确地模拟出射流器内部的流动状态,仿真结果与试验结果吻合较好,从而建立了射流器设计的计算流体力学仿真模式。
图1 为射流器的基本结构图。由水泵供给的工作水流通过进水管流入射流器,并经过喷嘴喷射出去,形成高速的水射流,在喷嘴的周围形成负压;进气室的负压将空气从进气口吸入,被水射流高速携带进入混合管。在混合管始端,水射流与被带入的空气流作相对运动,并合成为气水两相流,在混合管内液体与气体分子的冲击碰撞使高速运动的射流将能量传递给气体,空气在混合管内被加速和压缩。气液两相流进入扩散管后,气体已经被剪切成微小气泡分散在液体中,形成泡沫流,经扩散管排出射流器。

图1 射流器的结构
Fig.1 Schematic diagram of the ejector
按照索科洛夫[8]提出的经典设计理论进行射流器的设计,设计步骤略,设计计算的各个重要参数见表1。
表1 射流器计算结果和尺寸列表
Tab.1 The calculation and sizes of the ejector

注:表中的d1、d2、L均为圆整后的数值。
Note:The d1,d2,and L are all integer values.
参数parameter数值value工作水流量Q/(m3·h-1)气、液混合后两相流体的压力Pc/(N·m-2)喷射系数u0喷嘴直径d1/mm混合管直径d2/mm混合管长L/mm扩散管长L′/mm扩散角σ/(°) 25 10133 0.395 19 29 260 142 6
在设计计算中,混合管与喷嘴的截面积比是一个重要的参数,计算公式[8]为
其中:f1为喷嘴的截面积;f2为混合管的截面积; PP为喷嘴进口处的液体压力;PH为引射气体的压力;Pc为气、液混合后两相流体的压力。由此可见,混合管与喷嘴的截面积比直接影响气、水混合后两相流体的压力,对混合效果影响较大[13]。为此,将混合管在原设计的基础上进一步改变尺寸,通过CFD仿真的方法测定哪种截面积比是最佳值,再通过试验验证仿真结果。初步取混合管直径为23、25、27、29、31、34、36、40 mm,相对应的截面积比为1.47、1.73、2.01、2.33、2.66、3.20、3.59、4.43,分别对以上8种不同尺寸的射流器进行仿真。
利用Fluent软件的仿真过程大致按照如下步骤进行:
选择计算的数学模型→建立流场模型→网格划分→设置边界条件和求解参数→利用Fluent软件求解器求解计算→保存结果并进行后处理等。
3.1 数学模型
由于射流器内部主要是紊动的气液两相流,所以采用基于欧拉两相流下的标准κ-ε双方程模型进行计算,分别对气相和液相建立封闭的数学模型。标准κ-ε方程由Launder和Spalding提出,是从试验现象中总结出的半经验公式,也是目前使用最广泛、最有效的模型。将该模型用于计算大量的各种薄剪切层和回流效果较好,且不需要就不同情况修正模型参数。限制流(有壁面约束)中,雷诺剪切力最显著,此模型对于限制流特别有效[14],已成为工程流场计算中的主要工具。
标准的κ-ε双方程模型是通过补充微分方程的方法来获得紊流尺度L的,用来封闭雷诺方程的微分方程数达到两个[15]。其表达式如下:
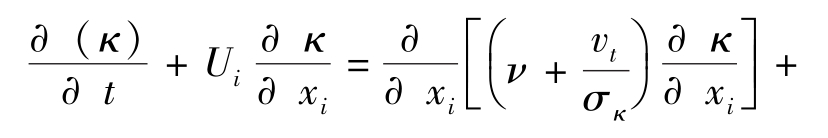
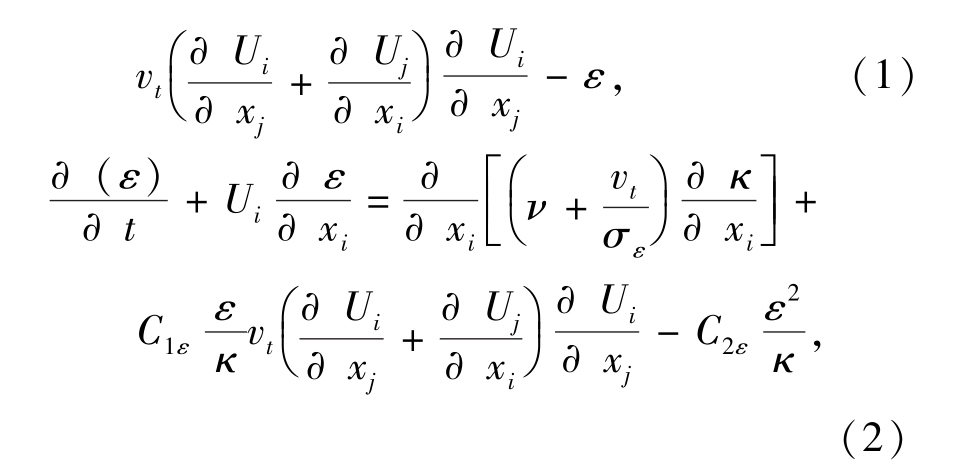
式中:t为时间;Ui、Uj分别为速度分量;xi、xj分别为坐标分量;C1ε、C2ε均为经验常数;σκ、σε分别表示与湍动能κ和耗散率ε对应的普朗特常数, ε=CDκ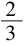 /l;涡粘系数vt=Cμκ2/ε。方程中5个可调常数取参考文献[15]中的值,即Cμ=0.09,C1ε=1.44,C2ε=1.92,σκ=1,σε=1.3。
/l;涡粘系数vt=Cμκ2/ε。方程中5个可调常数取参考文献[15]中的值,即Cμ=0.09,C1ε=1.44,C2ε=1.92,σκ=1,σε=1.3。
3.2 网格划分
根据射流器为回转体结构的特点,利用Fluent软件中的前处理软件Gambit作出其半截面形状即可,以简化计算。再利用Gambit将截面流场进行网格划分,采用四边形网格结构划分的混合管直径为23 mm的射流器流场区域如图2所示。

图2 模型的网格划分
Fig.2 Grid generation of the model
3.3 边界条件和求解参数的设置
在Gambit软件中为射流器的模型设置边界条件,工作水流入口为速度边界,取设计计算的速度值;空气入口和混合物出流口均为压力边界;液相与气相之间无滑移条件,壁面效应采用标准壁面函数法,含气率方程采用一阶迎风格式,速度压力的耦合方式采用Phase Coupled Simple算法,利用分离求解器(segregated solver)进行稳态计算,设定残差监视器,当计算残差小于10-3时认为计算结果达到收敛。
分别对8种不同截面积比的射流器进行CFD仿真,各个射流器流场的计算结果都达到规定的收敛条件,所用迭代步数从350步到650步不等,得到各个射流器的流场气相分布见图3。
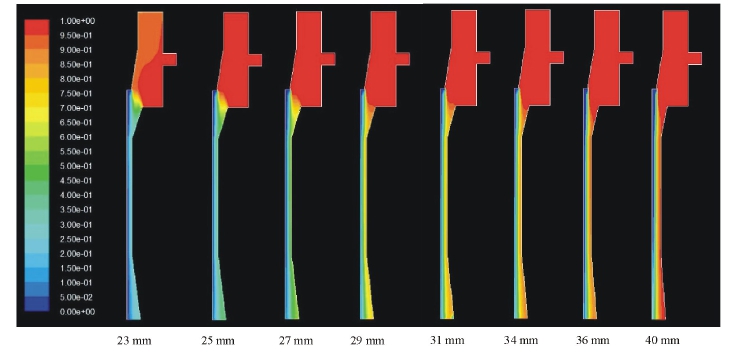
图3 8种混合管直径的射流器气相分布图
Fig.3 Contours of air volume fraction of eight mixing tube diameters
从图3可以看出,喷嘴所喷射出的高速水流在收缩段保持自己原来的形状,在收缩段和混合管的交界处产生激波。这是由于高速水流在交界处与引射的空气流交汇并碰撞壁面引起的。随着射流在混合管内与空气流混杂在一起,混合管内部形成气液两相流。当混合管的直径为23 mm时,管内的含气率较低,说明进气量很少,单位时间内溶解在水中的氧气也很少(在图中呈现蓝色);随着混合管直径的增大,空气在混合管内所占的比例不断升高,混合管内逐渐变成绿色或黄色,说明引射器所引射的空气流量增大,含气率较高;当混合管直径进一步增大到40 mm时,虽然混合管靠近右侧壁面处的含气率很高,呈现红色,但水射流在混合管大部分长度内却保持自己原来的形状,喷嘴中心线上射流的含气率为0,说明水射流与空气流分离,未与空气有效混合,此种情况下射流器起不到增氧的作用。
通过气相分布图的对比可以排除混合管直径为23 mm和40 mm两种混合效果很差的尺寸,在Fluent软件中查看剩余6种不同截面积比的射流器压力分布图,得到各个射流器混合管段的压力分布曲线如图4所示。
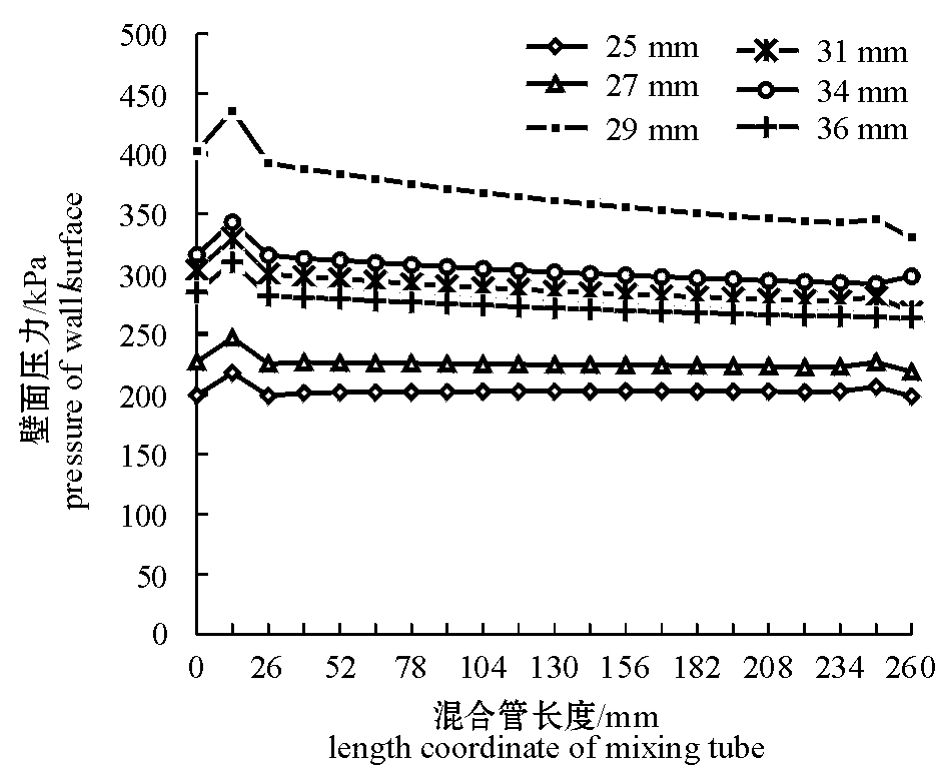
图4 混合管的壁面压力分布图
Fig.4 Distribution of wall surface pressure in a mixing tube
从图4可见,在收缩段与混合管的交界处产生压力跳跃,而后混合管内的压力变化趋于平缓。混合管直径从25 mm开始,壁面压力逐渐升高,直径为29 mm的射流器最高,直径超过29 mm时壁面压力逐渐下降。根据气体溶解于液体的亨利定律[16]C=P/K(式中:C为溶于溶剂内的气体摩尔浓度;P为气体的分压;K为气体的亨利常数),在气体溶解过程中,压力越大,溶解度就越高。仿真结果表明,当混合管直径为29 mm,截面积比为2.33时,混合管壁面压力最大。由此推断,此时的氧气溶解度最高,混合效果最好。
衡量混合管段气液混合程度的另一个参数是湍动动能。从图5可见,随着混合管直径的增加,湍动动能呈现先升后降的趋势,湍流程度在29 mm时达到最大,而后逐渐降低,这一结果证明了仿真所得出的混合效果趋势。
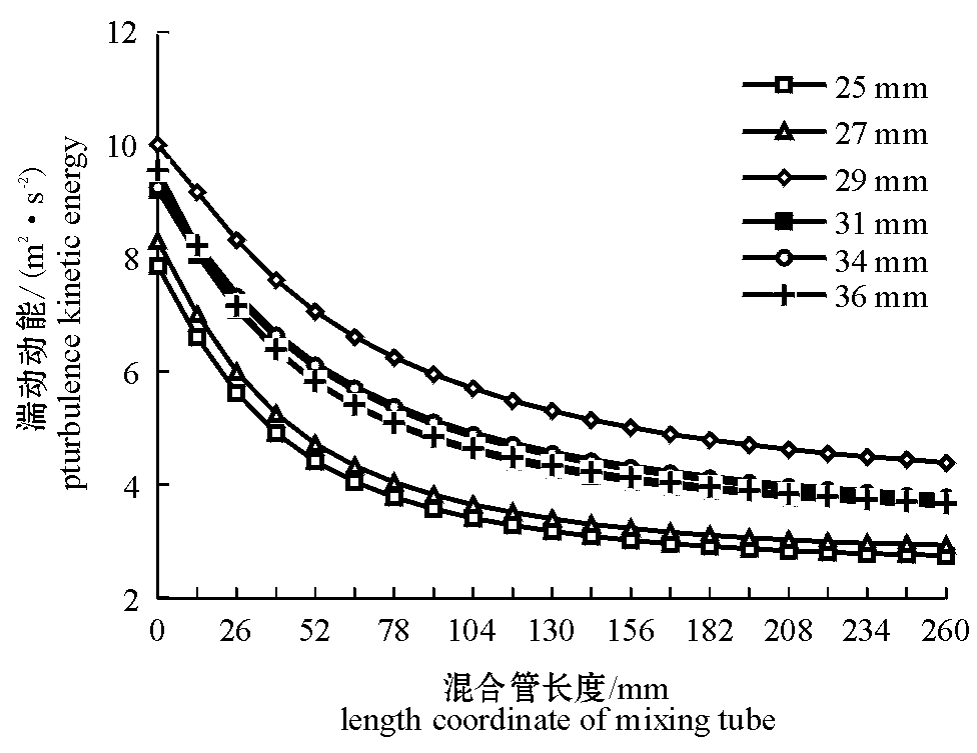
图5 混合管的湍动动能分布图
Fig.5 Distribution of turbulence kinetic energy in a mixing tube
在射流增氧的过程中,氧气与水体在射流混合管内形成两相流体,氧气在水中以气泡的形式运动,气泡越小,单位体积气体的溶解面积越大,溶解率就越高。根据湍流下气泡破碎的临界尺寸理论,若湍动动能大于表面张力,气泡就会破碎,变成小气泡。其气泡破碎的临界尺寸公式[15]表述如下:

式中:rc为气泡破碎的临界尺寸;σ为液体的表面张力;ρf为液体的密度;ρg为气体的密度;vr为湍动能的速度。
式(3)表明,湍动速度和动能越大,混合管中的两相流气泡的尺寸就越小,氧气溶解率就越高,混合效果越好。图5的CFD仿真结果表明,当喷嘴直径为19 mm,混合管直径为29 mm,二者截面积比为2.33时,湍动动能达到最大。由此可以推断,此时其氧气的溶解率最高,混合效果最好。
5.1 试验设备与方法
射流增氧验证试验在一个长、宽、高分别为2.58、1.04、1.00 m的水箱中进行,射流器的混合管设计成可拆卸结构,用有机玻璃做成不同尺寸的6种混合管,分别对每个混合管做两次试验(图6)。射流器的扩散管出口置于水箱平面,保证射流器的背压为一个大气压力。潜水泵与射流器分别位于水箱的两侧,使箱内的水能够不断循环;在水箱水体的中部布置带有温度补偿功能的溶解氧传感器,监视水中的溶解氧变化情况,型号为汉密尔顿Oxysens120,DO饱和度的测量范围为0~100.0%,测量精度为±0.2%,对应输出电流为4~20 mA。通过西门子公司的S7-200型可编程控制器(PLC)采集传感器数据,并通过通信电缆传输给上位机;上位机为商用计算机,安装组态王监控软件,能够自动记录传感器的输出信号变化,并绘制变化曲线图,信号采集间隔为1 s。
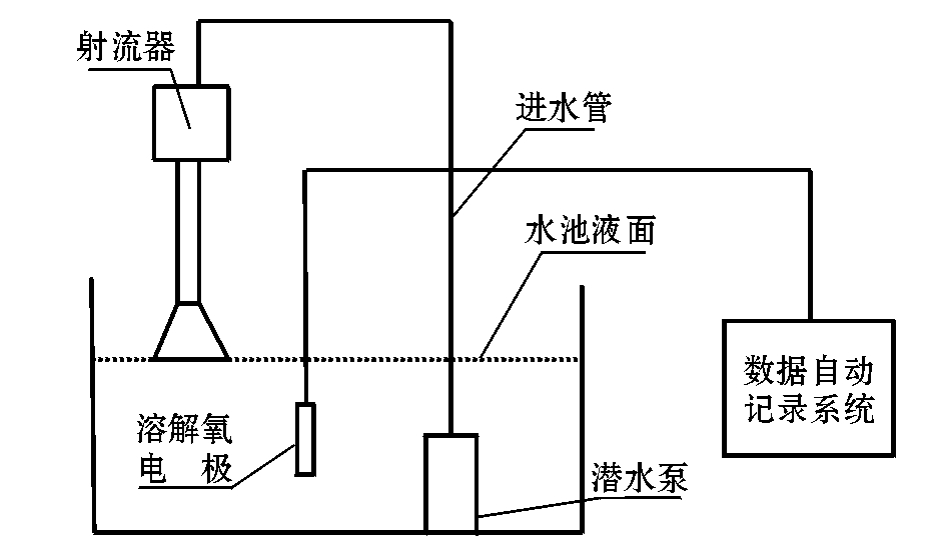
图6 试验设备布局示意图
Fig.6 Schematic layout of the equipments
溶解氧传感器自带有温度补偿功能,可忽略温度变化对溶解度的影响,射流器的混合效果由试验水体溶解氧上升的速度来衡量。试验用水为曝气沉淀后的自来水,水体容积为2.5 m3。试验开始前使用消氧药剂亚硫酸钠对水体进行消氧,使用氯化钴作为催化剂,加药量参考文献[9]。加药后搅拌池水直到溶解氧传感器的读数显示为0,此时开启潜水泵,射流器开始工作,数据采集系统自动记录溶解氧饱和度的变化,当水体溶解氧饱和度达到75%时关闭潜水泵,一次试验结束。第二次试验重复以上步骤,所有试验结果取平均值。
5.2 试验数据
试验数据可从组态王软件导入Excel中进行分析,以溶解氧饱和度从0上升至75%所用的时间t (min)为指标,对不同直径的6种混合管进行充氧试验,得出不同的时间如图7所示。
从图7可见,随着混合管直径的不断增加,增氧时间呈现先降后升的趋势,说明射流器的混合效果先变好后变差。当混合管直径为29 mm时,所用的增氧时间最短。
根据试验过程得到的数据,依据SC/T6009-1999增氧机试验计算方法,可由下列公式计算射流器的增氧能力:
式中:QS为增氧能力(kg/h);KLa(20)为标准条件下氧质量转移系数(h-1);V为试验水体体积(m3);CS(S)为标准标准条件下氧在水中的溶解度(mg/L3)。
由此得到增氧能力在不同混合管条件下的变化曲线(图7)。从图7可见,射流器增氧能力随着混合管直径变化为先升后降,当直径为29 mm时,其增氧能力值最大,射流器可达到最好增氧效果。
射流器增氧时间和增氧能力的试验表明,直径29 mm为混合管的最佳尺寸。与利用Fluent软件进行CFD仿真数值计算的结果相一致。由此证明了数值模拟与试验结果吻合较好。

图7 不同直径混合管的增氧时间和增氧能力
Fig.7 The oxygen transfer capability and period of different mixing tubes
国内很多学者通过试验找出射流器的尺寸与混合效果的关系,如庞云芝等[17]研制了一种应用于冰下和深水的射流式增氧机,通过试验探讨了设计尺寸与性能的关系;吴世海[2]通过试验筛选了影响射流式增氧机吸气量和动力效率的部件,但在设计之后并没有进行数值仿真,是典型的设计—制造—试验的模式。本研究中在设计射流式增氧装置后进行了计算流体动力学的仿真,对所设计的尺寸和工作状态进行了比较分析,使后来的制造和试验有了保证,形成了设计—仿真—比较分析—制造—试验的新方法。
运用κ-ε双方程模型对空气-水引射器内部流场进行数值模拟,得到射流器工作时内部流场的气相分布图和压力分布图,揭示了混合管内部的流动状态,能够直观地分析混合情况的好坏,为研制射流增氧设备提供了参数优化的新方法,并通过数值模拟对产品的性能进行准确的预测。
射流器混合管与喷嘴的截面积比是设计时的重要参数,与混合效果有着密切的关系。本研究中通过改变混合管的直径,对不同截面积比的射流器进行了数值模拟,找出了截面积比与混合效果之间的变化规律,确定了混合效果最好的一组尺寸,并进行射流器充氧验证试验。充氧试验的数据证明,数值仿真得出的变化规律是正确的,而且通过仿真确定的混合效果最好的尺寸即是试验效果最好的尺寸,说明射流器的CFD仿真是有效、可靠的。
参考文献:
[1] 陈维平,江帆,李元元,等.射流曝气的气液两相流的数值模拟[J].环境污染治理技术与设备,2006,7(3):48-52.
[2] 吴世海.射流自吸式增氧机[J].农业机械学报,2007,38(4): 88-92.
[3] 杨燕勤,安志强,经树栋.喉嘴距、面积比和引射压力对喷射器性能影响的研究[J].化工装备技术,2006,27(1):68-72.
[4] Rusly E.Ejector cooling with reference to combined ejector-vapour compression system[D].Melbourne:University of Melbourne, 2004.
[5] Sun Dawen.Comparative study of the performance of an ejector refrigerant cycle operating with various refrigerants[J].Energy Conversion&Management,1994,40:873-884.
[6] 陈文召,李光明,董有,等.供气式气液双喷嘴射流器的充氧性能研究[J].工业水处理,2007,27(7):33-37.
[7] 张于峰,赵薇,田琦,等.喷射器性能及太阳能喷射制冷系统工质的优化[J].太阳能学报,2007,28(2):130-136.
[8] 索科洛夫E Я,津格尔H M.喷射器[M].北京:科学出版社, 1977:193-219.
[9] 中华人民共和国农业部.中华人民共和国水产行业标准.SC/T 6009—1999增氧机增氧能力试验方法[S].
[10] 龚道童,吴应湘,郑之初,等.变质量流量螺旋管内两相流数值模拟[J].水动力学研究与进展,2006,21(5):640-645.
[11] 周建来,邱白晶,郑铭.双侧吸气射流增氧机内吸气作用的分析[J].农业工程学报,2009,25(7):72-78.
[12] 胡金榜,李艳平,陈安新,等.循环流化床脱硫反应器入口结构对气体流动影响数值模拟[J].化学工程,2005,33(1):20-23.
[13] 周建来,邱白晶,郑铭.双侧吸气射流增氧机的增氧性能试验[J].农业机械学报,2008,39(8):70-73.
[14] 李万平.计算流体力学[M].武汉:华中科技大学出版社, 2004:49-60.
[15] 郭烈锦.两相与多相流体动力学[M].西安:西安交通大学出版社,2002:430-439,584-591.
[16] The Chemical Association of Japan.Handbook of Chemical Engineering[M].Tokyo:Iwanami Publisher,1988:6-13.
[17] 庞云芝,李秀金.水-空气引射式冰下深水增氧机的设计与性能试验研究[J].农业工程学报,2003,19(3):112-115.
Numerical simulation and experiment in the design of a jet aerator based on Fluent
JIA Hui-wen1,2,CAO Guang-bin1,JIANG Shu-yi1,HAN Shi-cheng1,CHEN Zhong-xiang1
(1.Heilongjiang River Fisheries Research Institute,Chinese Academy of Fishery Sciences,Harbin 150070,China; 2.College of Engineering,Shanghai Ocean University,Shanghai 201306,China)
Abstract:The κ-ε two-equation turbulence model was applied to simulate the internal fluid field in a jet aerator designed by the authors.The parameter patterns within the fluid field revealed the flowing state in the mixing tube, which provided a reliable approach for parameter optimization and performance prediction of the jet aerator.The analysis of the data of numerical simulation indicated that the optimal area ratio was 2.33.The oxygen transfer experiment proved that the numerical simulation was in the same line with the experimental results.
Key words:jet aerator;numerical simulation;area ratio
文章编号:2095-1388(2011)03-0247-06
中图分类号:S969.32
文献标志码:A
收稿日期:2010-06-17
基金项目:科技部农业科技成果转化资金项目(2009GB23260451);黑龙江省科技计划项目(GA06B203);黑龙江水产研究所基本科研业务费项目(2009HSYZX-YZ-04)
作者简介:贾惠文(1984-),男,硕士研究生。E-mail:jhw20038152000@yahoo.com.cn
通信作者:曹广斌(1957-),男,研究员。E-mail:laocao@hotmail.com