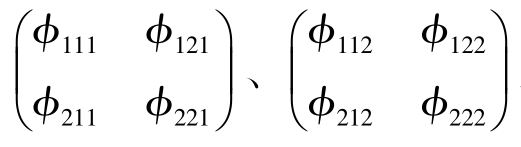为自回归参数矩阵;
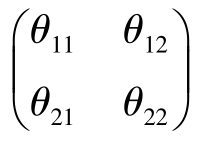为滑动平均参数矩阵;(εη)T为张丽梅1,王雪标2,李久奇3,王博3
(1.大连海洋大学理学院,辽宁大连116023;2.东北财经大学数学与数量经济学院,辽宁大连116025;3.大连海洋大学海洋工程学院,辽宁大连116023)
摘要：为了揭示国内海洋捕捞和海水养殖产量的相关关系,准确地跟踪并预测海洋捕捞和海水养殖产量的短期未来趋势,利用时序分析方法对1954—2006年国内海洋捕捞和海水养殖产量数据建立了多维自回归滑动平均(ARMAV)模型。该方法不仅避免了分别使用自回归滑动平均(ARMA)模型对两序列建模未考虑序列间关系的弊端,还通过数据的先期平稳化处理而使得算法的运用更具有针对性。图像与误差计算结果均表明,用本研究中给出的ARMAV(2,1,2)算法对两序列进行跟踪及预测具有效性。
关键词：海洋捕捞产量;海水养殖产量;平稳性;多维自回归滑动平均(ARMAV)模型
中国海洋捕捞业和海水养殖业历史悠久。早在夏代,沿海地区就采用网具、钩具开展海洋捕捞活动[1]。明代后期,东南沿海渔民已经有了牡蛎等贝类生物的养殖活动。新中国成立后特别是改革开放以来,伴随着海洋捕捞技术的不断发展与捕捞设备的不断进步,海洋捕捞产量大幅度增长。然而由于过度捕捞及全球海洋环境相关因素的影响,导致海洋渔业资源衰退,国内海洋捕捞产量在1999—2000年达到高峰后开始缓慢下滑。而海水养殖业伴随着海带育苗和养殖及坛紫菜养殖和栽培的成功,海珍品等海水养殖生物的遗传改良和新品种培育的技术突破,海水养殖生物营养机理、病原病理、养殖生态以及现代生物技术的研究与应用等方面取得了显著成绩[2]。与此同时,海水养殖面积不断扩大,海水养殖产量在经历20世纪50～70年代的缓慢增长后,从80年代中期开始呈现快速增长态势,产量由1954年的15.37万t增长到2006年1445.64万t,增长幅度近100倍。中国已成为世界海水养殖大国。
在海洋捕捞与海水养殖总量不断增加的同时,其时间序列数据组所表现出的内在数学关系,对有关部门制定可持续发展战略以及对研究人员从事科学研究均有重要意义。周井娟等[3-4]分别对国内海洋捕捞产量以及海水养殖产量进行了分析,在分别单一使用ARMA模型以及Logistic模型拟合的基础上,重点对实证进行了分析,但两序列之间的相关关系并未在模型建立时得到很好的体现。事实上,两序列之间虽没有相互确定的关系,但数据的产生均受到当年的政治、经济、环境、人文、供需关系等诸多因素的影响,因此海水捕捞与海水养殖产量共同对未来两序列数据产生影响是合乎道理的。近年来,国内学者已经将多维自回归滑动平均(ARMAV)模型广泛应用于工农业生产的模型建立与分析中。如吴晓明等[5-6]分别建立了国内第一产业与第二产业、第三产业产值的ARMAV模型,得到的分析与预测效果很好。本研究中,作者利用两序列建立的ARMAV模型,对1954—2006年中国海洋捕捞总产量(blt)和海水养殖总产量(yzt)的预测值(1954—1997年的数据是按全国水产品产量新标准计量的[7],而从1998—2006年中国水产统计年鉴中的资料沿用了这个标准,数据统计具有统一性)与实际值进行了比较,旨在揭示两序列的相互作用对未来产量数据共同影响的内在关系。
由于虚假回归问题的存在,在回归模型中应避免直接使用不存在协积关系的非平稳变量,因此检验变量的平稳性是一个必须解决的问题。通过Eviews软件对海洋捕捞和海水养殖产量分别进行严格的序列平稳性的统计检验——单位根检验,在对二阶差分数据进行单位根检验时得到平稳的时间序列bt、yt,数据见表1第4、5列。分别检验海洋捕捞、海水养殖二阶差分数据的自相关与偏自相关图,粗略获知其自回归部分的阶数为2。按照通常的做法,当自回归部分的阶数为2时,滑动平均部分的阶数定为1。这样,依据时间系列分析理论,借助Eviews软件,确定适合本研究数据的多维自回归滑动平均模型为ARMAV(2,1,2)。
设(bi,yt)T(t=1,2,…,N)表示第N个年份的海洋捕捞二阶差分数据bt以及海水养殖二阶差分数据yt。则所建立的模型为其中: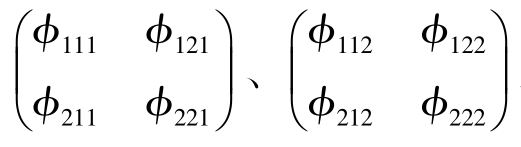为自回归参数矩阵;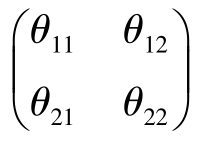为滑动平均参数矩阵;(εη)T为
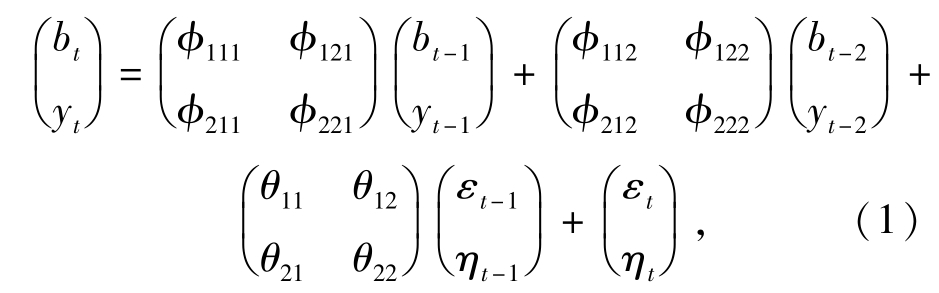
tt白噪声向量。故(εtηt)T应满足E((εt,ηt)T) =0,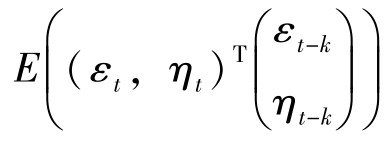
=δkQ,E为数学期望,Q为(εtηt)T的方差矩阵,
。
为了更好地控制噪声序列,先建立一个ARV (3,2)模型:
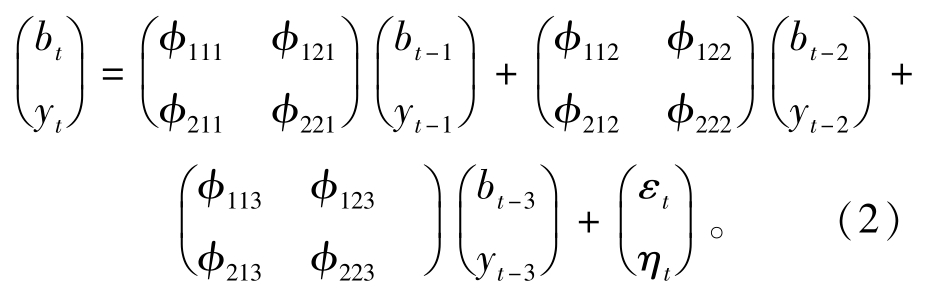
取t=4,5,…,N(这里可以取t≥4)。
对式(2)进行分析和整理得到
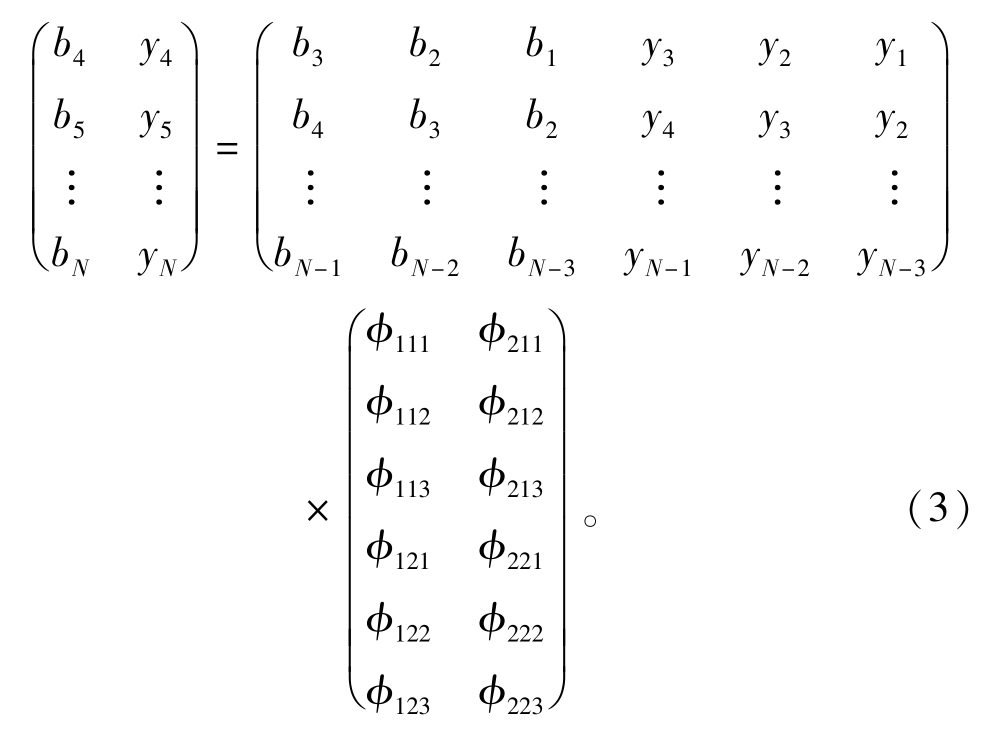
简记式(3)为矩阵方程X=WΦ。由于(bt,yt)T(t=1,2,…,N)为已知,由最小二乘法计算得知Φ=(WTW)-1WTX,具体计算结果为
将其带入式(2),得到估计的噪声序列(εtηt)T(t=4,5,…,N),将其具体结果带回到式(1),整理式(1)得到
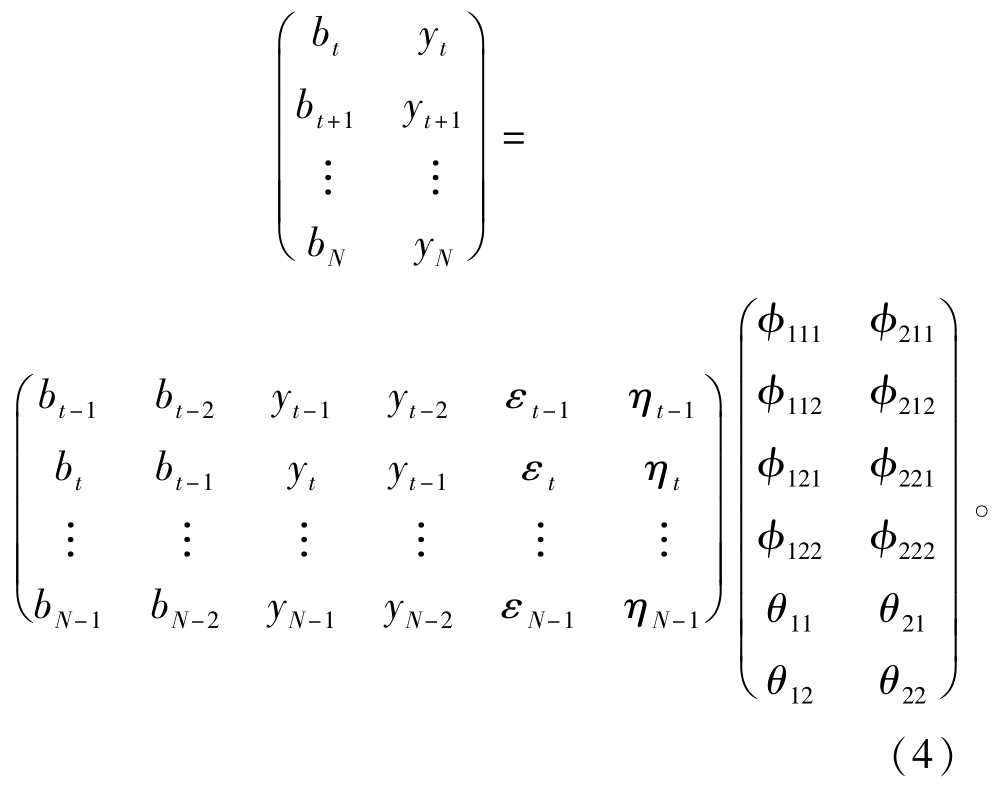
将估计的噪声序列(εtηt)T(t=4,5,…, N)用于式(4)的计算,此处t=5。简记式(4)为矩阵方程X1=W1Φ1,同样由最小二乘法得到Φ1=(W1TW1)-1W1TX1,将计算结果Φ1带入式(1),得到所建立模型的具体表达式为
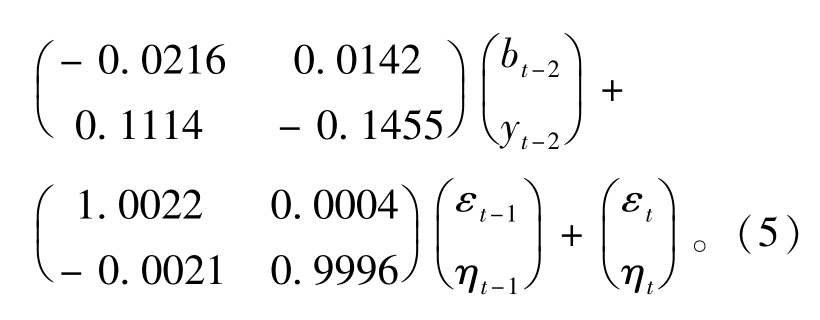
应用此模型对海洋捕捞与海水养殖二阶差分数据预测得到(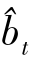
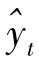)T,将其返回到海洋捕捞与海水养殖产值数据进行预测得到预测结果(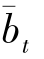
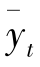)T,具体内容见表1第6至第9列。
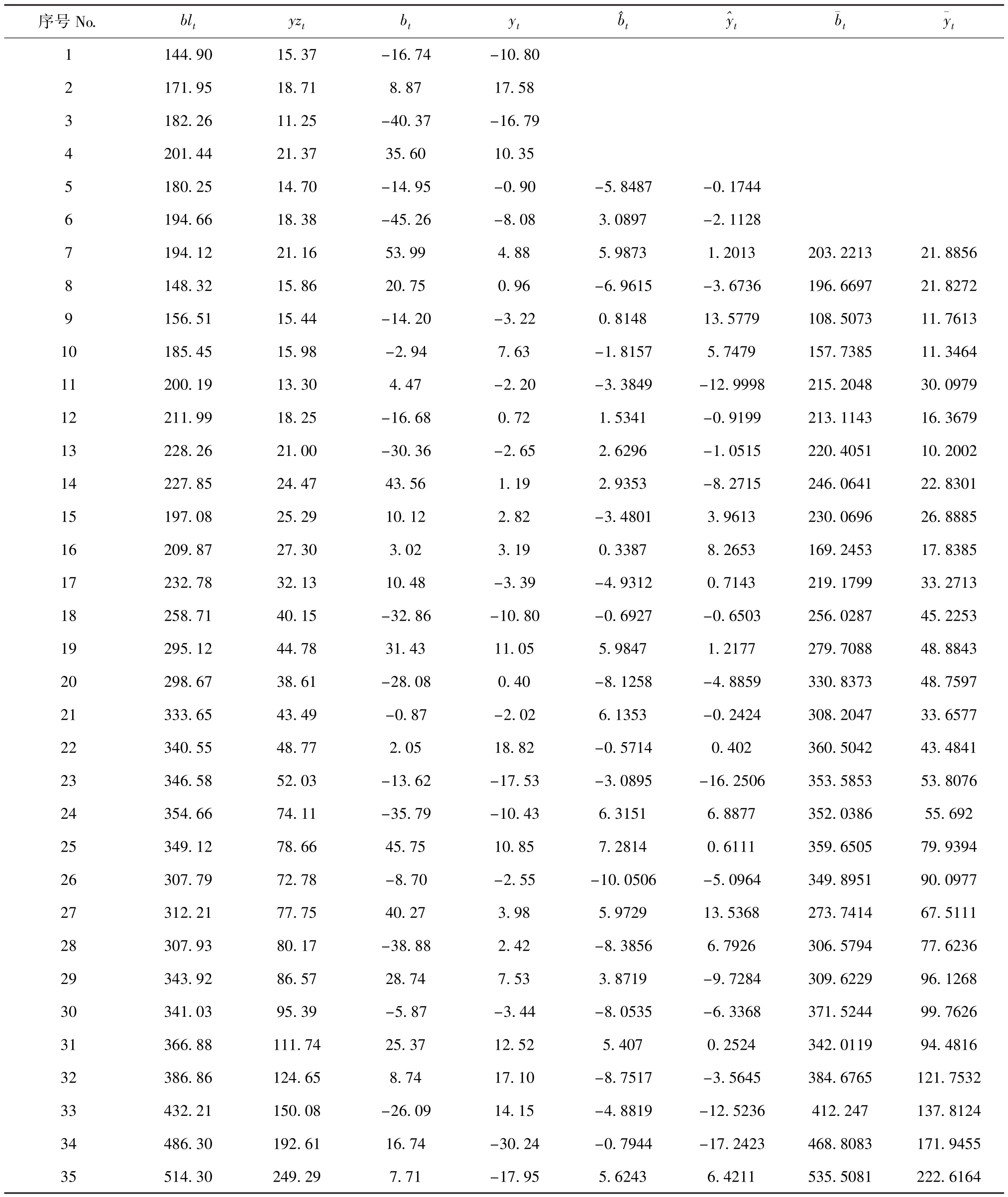
表1 1954—2006年国内海洋捕捞产量与海水养殖产量的预测值与实际值的比较
Tab.1 The comparison of the real values with the forecasting values in marine capture production and mariculture production in China from 1954 to 2006万t
序号No.bltyztbtyt^bt^yt¯bt¯yt1 144.9015.37-16.74-10.80 2 171.9518.718.8717.58 3 182.2611.25-40.37-16.79 4 201.4421.3735.6010.35 5 194.1221.1653.994.885.98731.2013203.221321.8856 8 148.3215.8620.750.96-6.9615-3.6736196.669721.8272 9 156.5115.44-14.20-3.220.814813.5779108.507311.7613 10185.4515.98-2.947.63-1.81575.7479157.738511.3464 11200.1913.304.47-2.20-3.3849-12.9998215.204830.0979 12211.9918.25-16.680.721.5341-0.9199213.114316.3679 13228.2621.00-30.36-2.652.6296-1.0515220.405110.2002 14227.8524.4743.561.192.9353-8.2715246.064122.8301 15197.0825.2910.122.82-3.48013.9613230.069626.8885 16209.8727.303.023.190.33878.2653169.245317.8385 17232.7832.1310.48-3.39-4.93120.7143219.179933.2713 18258.7140.15-32.86-10.80-0.6927-0.6503256.028745.2253 19295.1244.7831.4311.055.98471.2177279.708848.8843 20298.6738.61-28.080.40-8.1258-4.8859330.837348.7597 21333.6543.49-0.87-2.026.1353-0.2424308.204733.6577 22340.5548.772.0518.82-0.57140.402360.504243.4841 23346.5852.03-13.62-17.53-3.0895-16.2506353.585353.8076 24354.6674.11-35.79-10.436.31516.8877352.038655.692 25349.1278.6645.7510.857.28140.6111359.650579.9394 26307.7972.78-8.70-2.55-10.0506-5.0964349.895190.0977 27312.2177.7540.273.985.972913.5368273.741467.5111 28307.9380.17-38.882.42-8.38566.7926306.579477.6236 29343.9286.5728.747.533.8719-9.7284309.622996.1268 30341.0395.39-5.87-3.44-8.0535-6.3368371.524499.7626 31366.88111.7425.3712.525.4070.2524342.011994.4816 32386.86124.658.7417.10-8.7517-3.5645384.6765121.7532 33432.21150.08-26.0914.15-4.8819-12.5236412.247137.8124 34486.30192.6116.74-30.24-0.7944-17.2423468.8083171.9455 35514.30249.297.71-17.955.62436.4211535 180.2514.70-14.95-0.90-5.8487-0.1744 6 194.6618.38-45.26-8.083.0897-2.1128 7 .5081222.6164
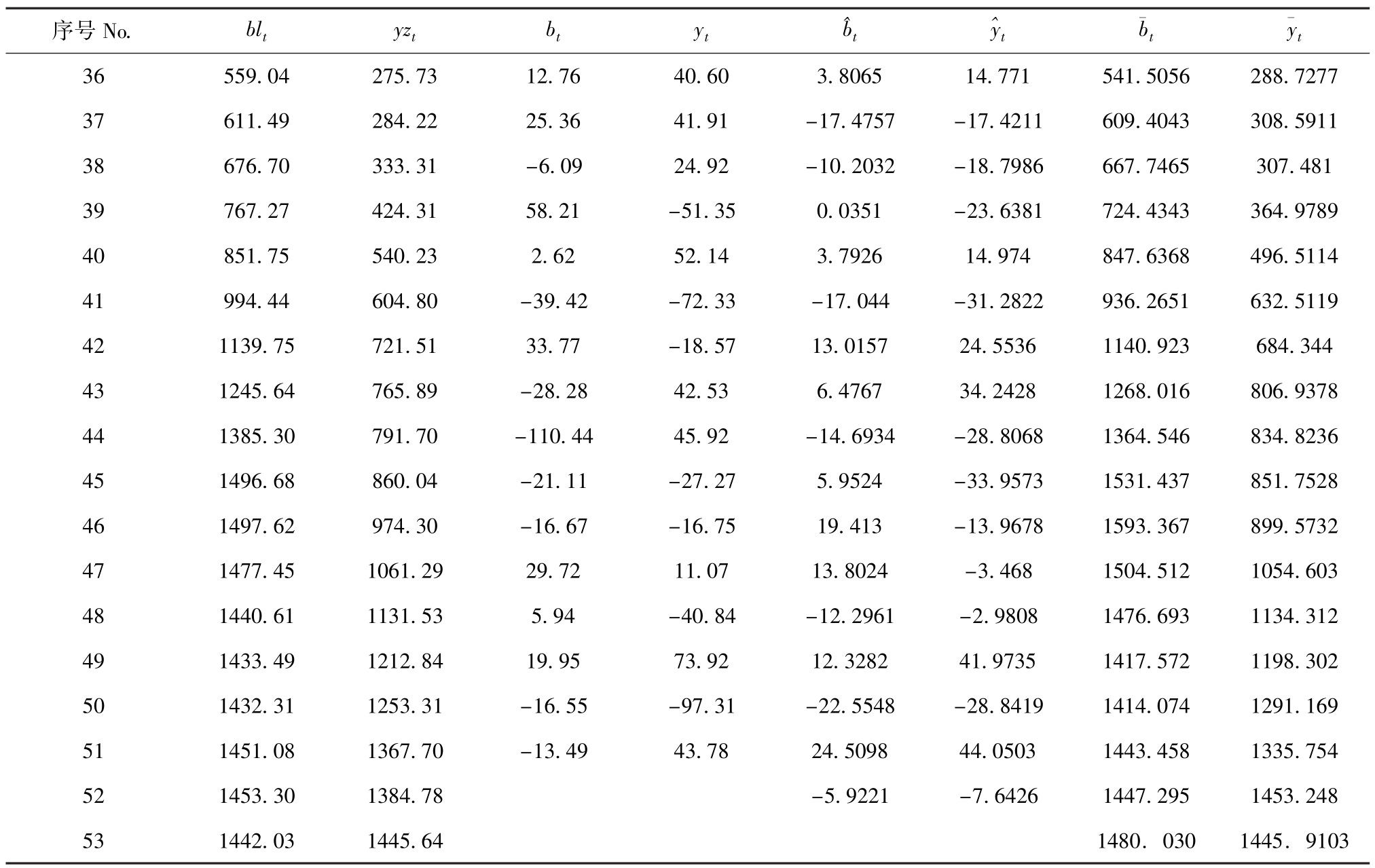
续表1 1954—2006年国内海洋捕捞产量与海水养殖产量的预测值与实际值的比较
Cont.Tab.1 The comparison of the real values with the forecasting values in marine capture production and mariculture production in China from 1954 to 2006万t
序号No.bltyztbtyt^bt^yt¯bt¯yt36559.04275.7312.7640.603.806514.771541.5056288.7277 37611.49284.2225.3641.91-17.4757-17.4211609.4043308.5911 38676.70333.31-6.0924.92-10.2032-18.7986667.7465307.481 39767.27424.3158.21-51.350.0351-23.6381724.4343364.9789 40851.75540.232.6252.143.792614.974847.6368496.5114 41994.44604.80-39.42-72.33-17.044-31.2822936.2651632.5119 421139.75721.5133.77-18.5713.015724.55361140.923684.344 431245.64765.89-28.2842.536.476734.24281268.016806.9378 441385.30791.70-110.4445.92-14.6934-28.80681364.546834.8236 451496.68860.04-21.11-27.275.9524-33.95731531.437851.7528 461497.62974.30-16.67-16.7519.413-13.96781593.367899.5732 471477.451061.2929.7211.0713.8024-3.4681504.5121054.603 481440.611131.535.94-40.84-12.2961-2.98081476.6931134.312 491433.491212.8419.9573.9212.328241.97351417.5721198.302 501432.311253.31-16.55-97.31-22.5548-28.84191414.0741291.169 511451.081367.70-13.4943.7824.509844.05031443.4581335.754 521453.301384.78-5.9221-7.64261447.2951453.248 531442.031445.641480.0301445.9103
表1 中:序号1～53分别对应1954—2006年; blt表示第t年的海洋捕捞产量;yzt表示第t年的海水养殖产量;bt、yt分别表示海洋捕捞、海水养殖产量的二阶差分数据,其计算公式为
bt=blt+2-2blt+1+blt,
yt=yzt+2-2yzt+1+yzt;
、
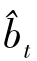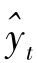分别为经本文给出的ARMAV(2,1,2)模型(式(5))对bt、yt进行预测所获得的结果;
、
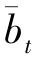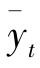是在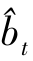
、
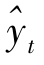基础上对blt、yzt的预测结果,其计算公式为
海洋捕捞产量和海水养殖产量的实际值与其跟踪预测值的比较见图1。
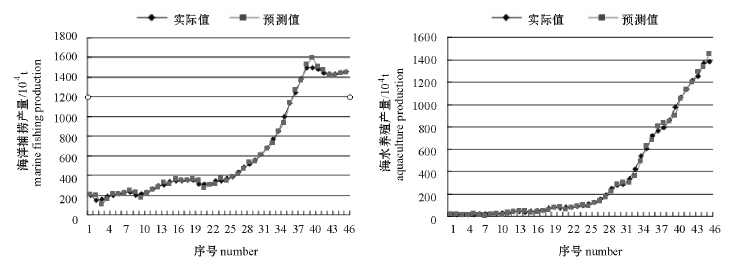
图1 海洋捕捞产量和海水养殖产量的实际值与经算法式(5)给出的预测值的比较
Fig.1 Comparison of the marine capture production,and the mariculture production with the forecast values
利用模型式(5)可以对后续年份的海洋捕捞产量以及海水养殖产量进行短期动态预测,但由于实际产量受到自然环境、政治经济等诸多因素的影响,所以预测产生一定程度的偏差是必然的。
本研究中通过计算方差矩阵进行误差分析,先利用模型式(5)对2007年海洋捕捞与海水养殖产量进行预测,分别得到预测值1424.88万t和1499.267万t。设海洋捕捞与海水养殖预测值与实际值的残差序列分别为be={bet},ye={yet},其中bet=bt-blt,yet=yt-yzt,通过计算得到be与ye的方差矩阵为
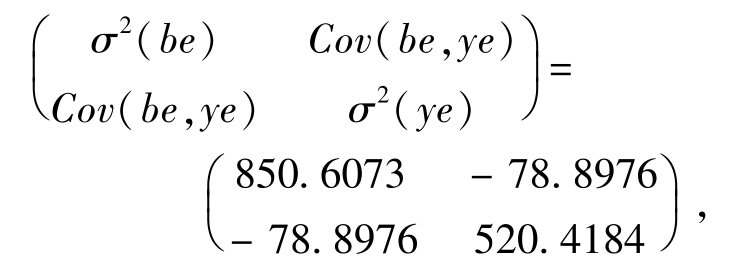
其中:σ2为方差;Cov为协方差。
本研究中从海水养殖与海洋捕捞产量的相互关系出发,建立了多维自回归滑动平均ARMAV(2, 1,2)模型,并使用它对中国海洋捕捞与海水养殖产量进行了跟踪和预测,其时间序列数据组所表现出的内在数学关系对有关研究人员从事科学研究具有重要意义。
该方法避免了分别单一对海洋捕捞与海水养殖产量进行跟踪和预测所导致的片面性,对综合考虑两者之间的关系提供算法分析原理与数据支持,也为进一步用多指标研究两者之间的关系奠定了基础。
致谢:在本研究过程中受到大连海洋大学刘焕亮教授的热忱指导,在此深表谢意!
参考文献：
[1] 乐佩琦,梁秋荣.中国古代渔业史源和发展概述[J].动物学杂志,1995,30(4):54-58.
[2] 刘焕亮,黄樟翰.中国水产养殖学[M].北京:科学出版社, 2008:1-45.
[3] 周井娟,林坚.我国海洋捕捞产量波动影响因素的实证分析[J].经济技术,2008,27(6):64-68.
[4] 周井娟,林坚.我国海水养殖产量波动影响因素的实证分析[J].西北农林科技大学学报,2008,8(5):48-51.
[5] 吴晓明,关蓬莱.多维自回归平均模型研究与应用[J].辽宁大学学报:自然科学版,2002,29(1):22-27.
[6] 吴晓明,盛元生.国内第三产业产值的ARMAV模型研究与应用[J].数学的实践与认识,2002,32(6):926-932.
[7] 历年全国水产品产量新旧标准统计对照表[J].中国水产, 1998,9:60.
The analysis of marine capture production and mariculture production in China by ARMAV models
ZHANG Li-mei1,WANG Xue-biao2,LI Jiu-qi3,WANG Bo3
(1.School of Science,Dalian Ocean University,Dalian 116023,China;2.College of Math and Quantitative Economics,Dongbei University of Finance&Economics,Dalian 116025,China;3.School of Marine Environmental Engineering,Dalian Ocean University,Dalian 116023,China)
Abstract：The auto-regressive moving average vector(ARMAV)models are established by the data of marine capture production and mariculture production in China from 1954 to 2006 to reveal the relationship between the marine capture production and mariculture production in China,tracking and forecasting accurately the short-term trend in future.The use of the ARMAV models here not only prevents the sickness of un-touching the relationship between the marine capture production and the mariculture production when using auto-regressive moving average(ARMA) models for the two sets of data respectively,but also makes the algorithm have pertinence after smoothness disposal of the data in advance.Both of the results of the images and the errors demonstrate the validity of the algorithm when tracking and forecasting the two data set by the ARMAV(2,1,2)models given in the paper.
Key words：marine capture production;mariculture production;smoothness;auto-regressive moving average vector(ARMAV)model
文章编号：2095-1388(2011)02-0157-05
中图分类号：F307.4
文献标志码：A
收稿日期：2010-05-05
基金项目：国家自然科学基金资助项目(10771028)
作者简介：张丽梅(1965-),女,博士,教授。E-mail:zlm@dlou.edu.cn